Tìm GTNN của \(A=x+\dfrac{1}{y}+\dfrac{4}{x-y}\) (với \(x>y>0\)).
SO
Những câu hỏi liên quan
1.cho x > 0. tìm GTNN của A = \(\dfrac{3x^4+16}{x^3}\)
2. cho x,y,z > 0 thỏa mãn x+y+z=2. tìm GTNN của biểu thức:
P=\(\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\)
giúp mình với ạ, mình đang cần gấp trong tối nay ạ.
kẻ lười biếng nạp card, đi ô tô
Đúng 0
Bình luận (0)
Tìm GTNN của P=\(\dfrac{x^4}{y^4}+\dfrac{y^4}{x^4}-\left(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}\right)+\dfrac{x}{y}+\dfrac{y}{x}\). Với x, y ≠ 0
Đặt \(\dfrac{x}{y}+\dfrac{y}{x}=t\Rightarrow\left|t\right|\ge2\)
\(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}=t^2-2\)
\(\dfrac{x^4}{y^4}+\dfrac{y^4}{x^4}=\left(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}\right)^2-2=\left(t^2-2\right)^2-2=t^4-4t^2+2\)
\(\Rightarrow P=f\left(t\right)=t^4-4t^2+2-\left(t^2-2\right)+t\)
\(f\left(t\right)=t^4-5t^2+t+4\)
Xét hàm \(f\left(t\right)=t^4-5t^2+t+4\) trên \((-\infty;-2]\cup[2;+\infty)\)
\(f'\left(t\right)=g\left(t\right)=4t^3-10t+1\)
\(g\left(t\right)\) bậc 3 nên có tối đa 3 nghiệm
\(g\left(-2\right)=-11\) ; \(g\left(0\right)=1\)
\(\Rightarrow g\left(-2\right).g\left(0\right)< 0\Rightarrow g\left(t\right)=0\) có nghiệm \(t_1\in\left(-2;0\right)\)
\(g\left(1\right)=-5< 0\Rightarrow g\left(0\right).g\left(1\right)< 0\Rightarrow g\left(t\right)\) có nghiệm \(t_2\in\left(0;1\right)\)
\(g\left(2\right)=13\Rightarrow g\left(1\right).g\left(2\right)< 0\Rightarrow g\left(t\right)\) có nghiệm \(t_3\in\left(1;2\right)\)
Dấu \(f'\left(t\right)\):
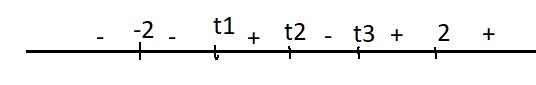
Từ đây ta thấy \(f\left(t\right)\) nghịch biến trên \((-\infty;-2]\) và đồng biến trên \([2;+\infty)\)
Hay GTNN của \(f\left(t\right)\) sẽ rơi vào \(t=-2\) hoặc \(t=2\)
\(f\left(-2\right)=-2\) ; \(f\left(2\right)=2\)
\(\Rightarrow f\left(t\right)_{min}=-2\) khi \(t=-2\) hay \(P_{min}=-2\) khi \(x=-y\)
Đúng 1
Bình luận (0)
tìm GTNN của A= 5x+\(\dfrac{13}{9}\)y+\(\dfrac{3}{x}\) +\(\dfrac{4}{y}\)
với x,y>0 và 2x+y > hoặc =5
Áp dụng BĐT cosi:
\(A=\left(3x+\dfrac{3}{x}\right)+\left(\dfrac{4}{9}y+\dfrac{4}{y}\right)+\left(2x+y\right)\\ A\ge2\sqrt{\dfrac{9x}{x}}+2\sqrt{\dfrac{16y}{9y}}+5\\ A\ge2\cdot3+2\cdot\dfrac{4}{3}+5=\dfrac{41}{3}\)
Vậy \(A_{min}=\dfrac{41}{3}\Leftrightarrow\left\{{}\begin{matrix}3x=\dfrac{3}{x}\\\dfrac{4y}{9}=\dfrac{4}{y}\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)
Đúng 1
Bình luận (1)
1. Tìm GTNN của \(y=x+\dfrac{1}{x}-5\) trên \(\left(0,+\infty\right)\)
2. Tìm GTNN của \(y=4x^2+\dfrac{1}{x}-4\) trên \(\left(0,+\infty\right)\)
3. Tìm GTLN của \(y=\dfrac{x^2+4}{x}\) trên \(\left(-\infty,0\right)\)
\(y=x+\dfrac{1}{x}-5\ge2\sqrt{\dfrac{x}{x}}-5=-3\)
\(y_{min}=-3\) khi \(x=1\)
\(y=4x^2+\dfrac{1}{2x}+\dfrac{1}{2x}-4\ge3\sqrt[3]{\dfrac{4x^2}{2x.2x}}-4=-1\)
\(y_{min}=-1\) khi \(x=\dfrac{1}{2}\)
\(y=x+\dfrac{4}{x}\Rightarrow y'=1-\dfrac{4}{x^2}=0\Rightarrow x=-2\)
\(y\left(-2\right)=-4\Rightarrow\max\limits_{x>0}y=-4\) khi \(x=-2\)
Đúng 0
Bình luận (0)
1. Cho \(x,y,z>0\) và \(x^3+y^2+z=2\sqrt{3}+1\). Tìm GTNN của biểu thức \(P=\dfrac{1}{x}+\dfrac{1}{y^2}+\dfrac{1}{z^3}\)
2. Cho \(a,b>0\). Tìm GTNN của biểu thức \(P=\dfrac{8}{7a+4b+4\sqrt{ab}}-\dfrac{1}{\sqrt{a+b}}+\sqrt{a+b}\)
1) Áp dụng bđt Cauchy cho 3 số dương ta có
\(\dfrac{1}{x}+\dfrac{1}{x}+\dfrac{1}{x}+x^3\ge4\sqrt[4]{\dfrac{1}{x}.\dfrac{1}{x}.\dfrac{1}{x}.x^3}=4\) (1)
\(\dfrac{3}{y^2}+y^2\ge2\sqrt{\dfrac{3}{y^2}.y^2}=2\sqrt{3}\) (2)
\(\dfrac{3}{z^3}+z=\dfrac{3}{z^3}+\dfrac{z}{3}+\dfrac{z}{3}+\dfrac{z}{3}\ge4\sqrt[4]{\dfrac{3}{z^3}.\dfrac{z}{3}.\dfrac{z}{3}.\dfrac{z}{3}}=4\sqrt{3}\) (3)
Cộng (1);(2);(3) theo vế ta được
\(\left(\dfrac{3}{x}+\dfrac{3}{y^2}+\dfrac{3}{z^3}\right)+\left(x^3+y^2+z\right)\ge4+2\sqrt{3}+4\sqrt{3}\)
\(\Leftrightarrow3\left(\dfrac{1}{x}+\dfrac{1}{y^2}+\dfrac{1}{z^3}\right)\ge3+4\sqrt{3}\)
\(\Leftrightarrow P\ge\dfrac{3+4\sqrt{3}}{3}\)
Dấu "=" xảy ra <=> \(\left\{{}\begin{matrix}\dfrac{1}{x}=x^3\\\dfrac{3}{y^2}=y^2\\\dfrac{3}{z^3}=\dfrac{z}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\sqrt[4]{3}\\z=\sqrt{3}\end{matrix}\right.\) (thỏa mãn giả thiết ban đầu)
Đúng 2
Bình luận (0)
2) Ta có \(4\sqrt{ab}=2.\sqrt{a}.2\sqrt{b}\le a+4b\)
Dấu"=" khi a = 4b
nên \(\dfrac{8}{7a+4b+4\sqrt{ab}}\ge\dfrac{8}{7a+4b+a+4b}=\dfrac{1}{a+b}\)
Khi đó \(P\ge\dfrac{1}{a+b}-\dfrac{1}{\sqrt{a+b}}+\sqrt{a+b}\)
Đặt \(\sqrt{a+b}=t>0\) ta được
\(P\ge\dfrac{1}{t^2}-\dfrac{1}{t}+t=\left(\dfrac{1}{t^2}-\dfrac{2}{t}+1\right)+\dfrac{1}{t}+t-1\)
\(=\left(\dfrac{1}{t}-1\right)^2+\dfrac{1}{t}+t-1\)
Có \(\dfrac{1}{t}+t\ge2\sqrt{\dfrac{1}{t}.t}=2\) (BĐT Cauchy cho 2 số dương)
nên \(P=\left(\dfrac{1}{t}-1\right)^2+\dfrac{1}{t}+t-1\ge\left(\dfrac{1}{t}-1\right)^2+1\ge1\)
Dấu "=" xảy ra <=> \(\left\{{}\begin{matrix}\dfrac{1}{t}-1=0\\t=\dfrac{1}{t}\end{matrix}\right.\Leftrightarrow t=1\)(tm)
khi đó a + b = 1
mà a = 4b nên \(a=\dfrac{4}{5};b=\dfrac{1}{5}\)
Vậy MinP = 1 khi \(a=\dfrac{4}{5};b=\dfrac{1}{5}\)
Đúng 1
Bình luận (0)
Cho x>0; y>0. Tìm GTNN của \(A=\sqrt{x}+\sqrt{y}\) biết \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{2}\).
Cho x,y > 0 thỏa mãn x+y=1 Tìm GTNN của P=\(\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{4}{xy}\)
Lời giải:
Áp dụng BĐT Bunhiacopxky:
$(\frac{1}{x^2}+\frac{1}{y^2}+\frac{2}{xy})(x^2+y^2+2xy)\geq (1+1+2)^2=16$
$\Rightarrow \frac{1}{x^2}+\frac{1}{y^2}+\frac{2}{xy}\geq \frac{16}{(x+y)^2}=16$
Áp dụng BĐT AM-GM:
$xy\leq \frac{(x+y)^2}{4}=\frac{1}{4}$
$\Rightarrow \frac{2}{xy}\geq 8$
Cộng 2 BĐT trên lại:
$P\geq 16+8=24$
Vậy $P_{\min}=24$ khi $x=y=\frac{1}{2}$
Đúng 2
Bình luận (0)
Lời giải:
Áp dụng BĐT Bunhiacopxky:
$(\frac{1}{x^2}+\frac{1}{y^2}+\frac{2}{xy})(x^2+y^2+2xy)\geq (1+1+2)^2=16$
$\Rightarrow \frac{1}{x^2}+\frac{1}{y^2}+\frac{2}{xy}\geq \frac{16}{(x+y)^2}=16$
Áp dụng BĐT AM-GM:
$xy\leq \frac{(x+y)^2}{4}=\frac{1}{4}$
$\Rightarrow \frac{2}{xy}\geq 8$
Cộng 2 BĐT trên lại:
$P\geq 16+8=24$
Vậy $P_{\min}=24$ khi $x=y=\frac{1}{2}$
*cách này đơn giản hơn
Vì x,y>0. theo AM-GM:
\(\dfrac{1}{x^2}\)+\(\dfrac{1}{y^2}\) ≥\(\dfrac{2}{xy}\) => P≥\(\dfrac{6}{xy}\)
ta có: \(x^2\)+\(y^2\)≥ 2xy <=> (x+y)\(^2\)≥4xy <=> xy≤\(\dfrac{\left(x+y\right)^2}{4}\)=\(\dfrac{1}{4}\)
<=> \(\dfrac{6}{xy}\)≥\(\)24 hay P≥24
dấu = xảy ra khi: x=y=\(\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
Tìm GTNN của A=\(\dfrac{x}{\sqrt{y}}+\dfrac{y}{\sqrt{z}}+\dfrac{z}{\sqrt{x}}\) với x,y,z>0 và \(x+y+z\ge12\)
\(A^2=\dfrac{x^2}{y}+\dfrac{y^2}{z}+\dfrac{z^2}{x}+2\left(\dfrac{xy}{\sqrt{yz}}+\dfrac{yz}{\sqrt{xz}}+\dfrac{xz}{\sqrt{xy}}\right)\)
Áp dụng BĐT cosi:
\(\dfrac{x^2}{y}+\dfrac{xy}{\sqrt{yz}}+\dfrac{xy}{\sqrt{yz}}+z\ge4\sqrt[4]{\dfrac{x^4y^2z}{y^2z}}=4x\)
\(\dfrac{y^2}{z}+\dfrac{yz}{\sqrt{xz}}+\dfrac{yz}{\sqrt{xz}}+x\ge4\sqrt[4]{\dfrac{y^4z^2x}{z^2x}}=4y\)
\(\dfrac{z^2}{x}+\dfrac{xz}{\sqrt{xy}}+\dfrac{xz}{\sqrt{xy}}+y\ge4\sqrt[4]{\dfrac{z^4x^2y}{x^2z}}=4z\)
Cộng VTV 3 BĐT trên:
\(\Leftrightarrow A^2+\left(x+y+z\right)\ge4\left(x+y+z\right)\\ \Leftrightarrow A^2\ge3\left(x+y+z\right)\ge3\cdot12=36\\ \Leftrightarrow A\ge6\)
Dấu \("="\Leftrightarrow x=y=z=\dfrac{12}{3}=4\)
Đúng 0
Bình luận (0)
Chứng minh với a, b lớn hơn 0 thì: \(\dfrac{a+b}{2}=\sqrt{ab}\). Áp dụng tìm GTNN của \(A=\dfrac{1}{x}+\dfrac{1}{y}\) biết x+y=1 và x, y dương
Ta có : \(\dfrac{a+b}{2}\ge\sqrt{ab}\Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\) ( luôn đúng )
Dấu "=" xảy ra khi \(a=b\)
Bài tập :
Có : \(A=\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{x+y}{x}+\dfrac{x+y}{y}=2+\dfrac{x}{y}+\dfrac{y}{x}\) ( do \(x+y=1\) )
Theo BĐT trên có : \(\dfrac{x}{y}+\dfrac{y}{x}\ge2.\sqrt{\dfrac{x}{y}\cdot\dfrac{y}{x}}=2\)
Nên \(A\ge2+2=4\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=\dfrac{1}{2}\)
Đúng 1
Bình luận (0)







