a) Vẽ lại hình đã cho
b) Ghi giả thiết và kết luận của định lí minh họa bởi hình vẽ
ghi giả thiết và kết luận của định lí minh hoạ bởi cách hình vẽ sau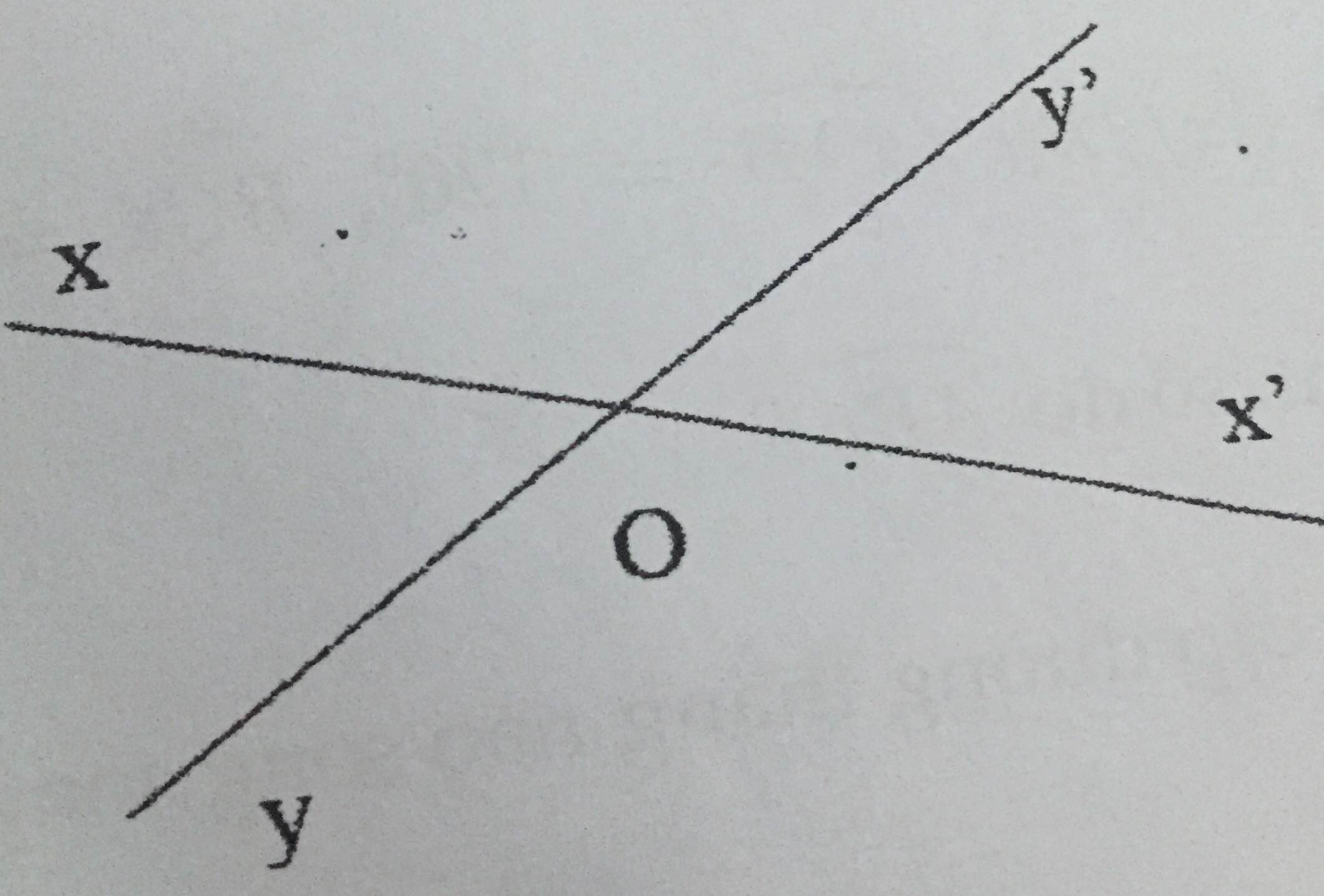
| GT | Ox đối Ox' ; Oy đối Oy' |
| KL | \(\widehat{xOy}=\widehat{x'Oy'};\widehat{xOy'}=\widehat{x'Oy}\) (các cặp góc đối đỉnh |
ghi giả thiết và kết luận của định lí minh hoạ bởi cách hình vẽ sau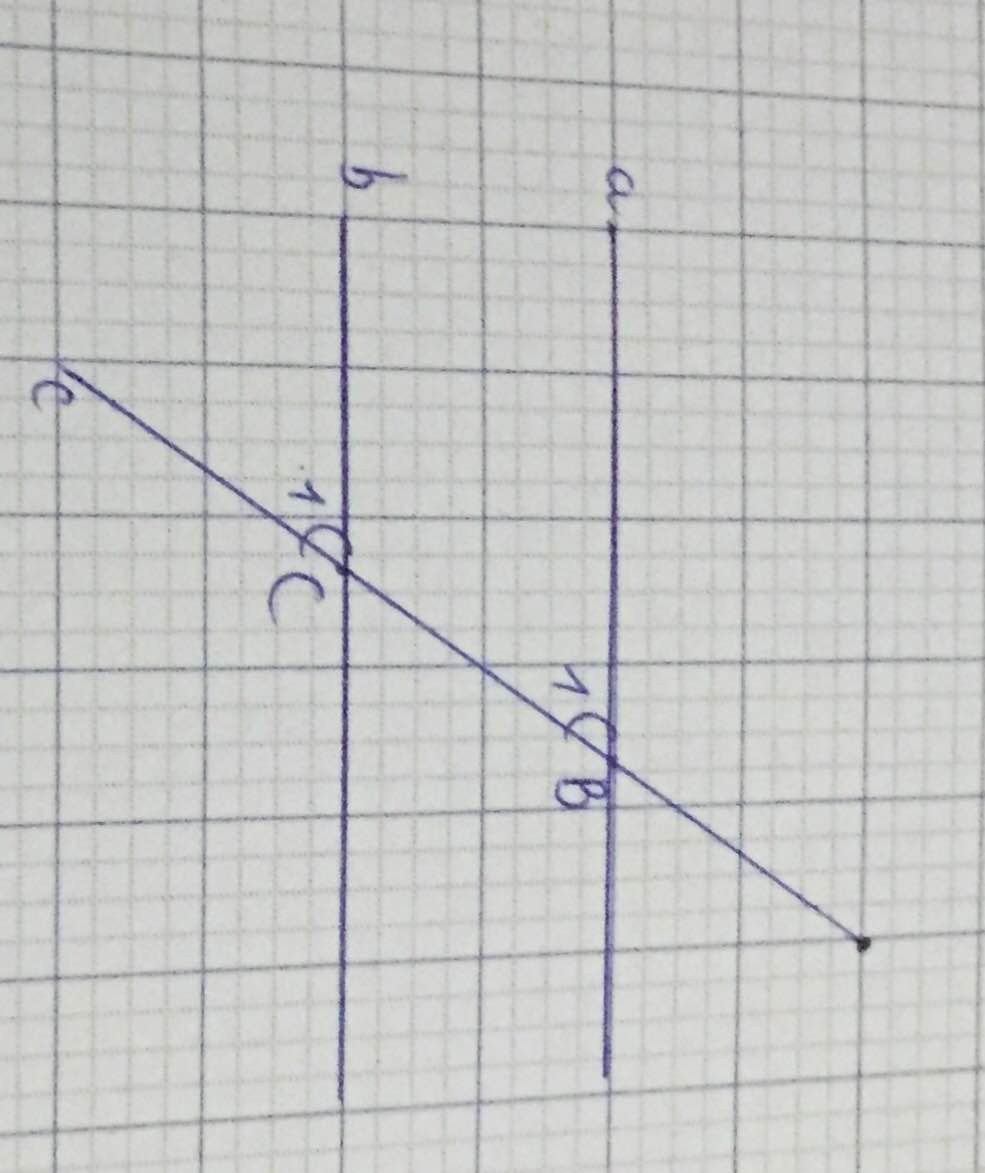
| GT | a//b |
| KL | \(\widehat{C_1}=\widehat{B_1}\) (2 góc đồng vị) |
ghi giả thiết và kết luận của định lí minh hoạ bởi cách hình vẽ sau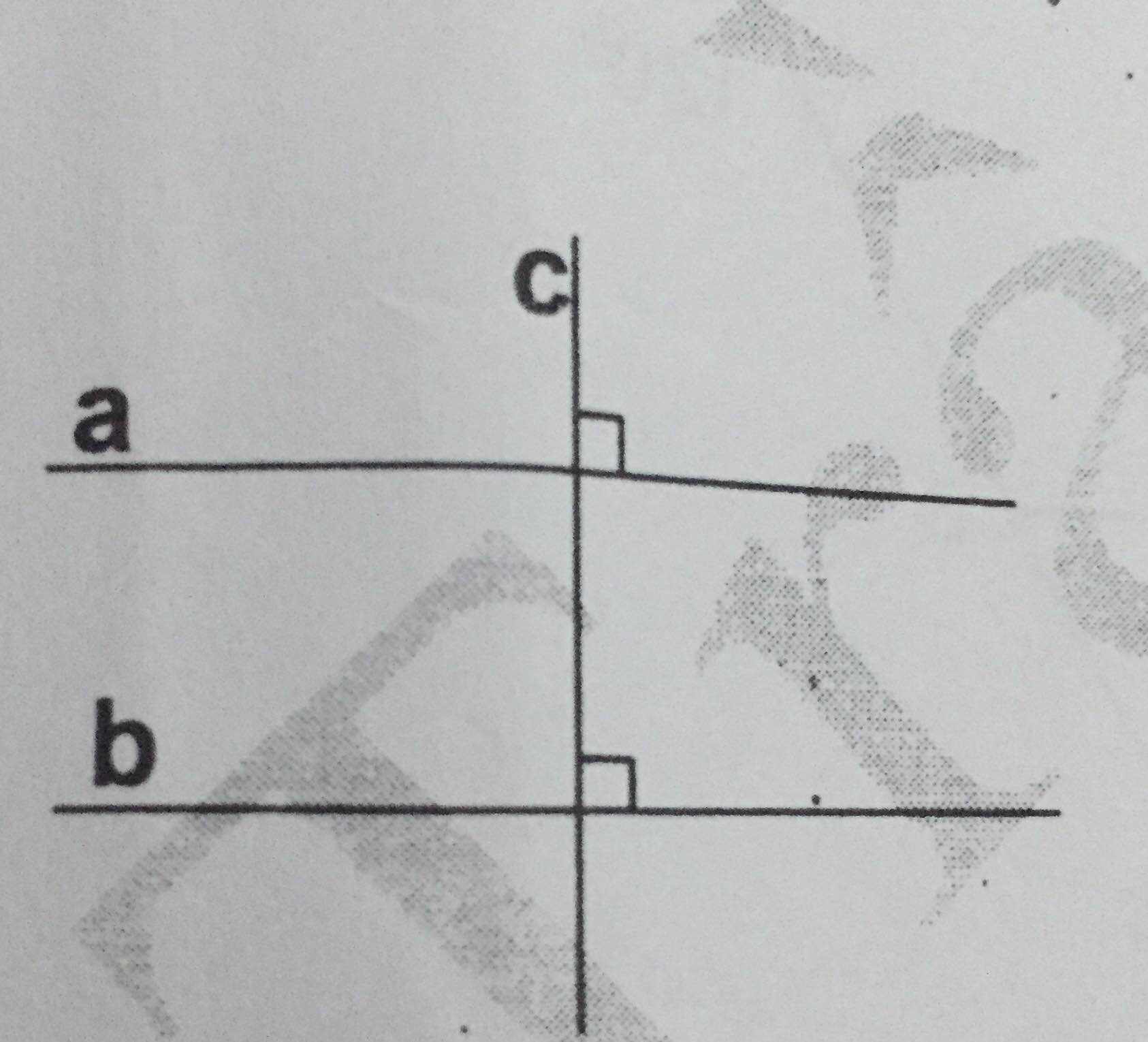
| GT | \(a\perp c;b\perp c\) |
| KL | \(a//b\) |
A) Hãy viết định lí nói về 1 đường thẳng vuông góc với một trong hai đường thẳng song song
B) Vẽ hình minh họa định lí đó và viết giả thiết,kết luận bằng kí hiệu
chỉ cần ghi định lí,giả thiết,kết luận thôi!
Vẽ hình minh họa định lí trên và viết, giả thiết kết luận bằng kí hiệu
hình vẽ minh họa
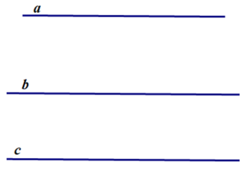
Giả thiết : a//c ; b//c
Kết luận : a//b
Vẽ hình minh họa định lí đó và viết giả thiết kết luận bằng cách kí hiệu.
Hình minh họa và viết giả thiết kết luận bằng kí hiệu:
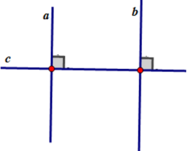
Giả thiết: a⊥c, b⊥c
Kết luận: a//b
1. Phát biểu, vẽ hình, ghi giả thiết - kết luận của định lí Ta-let, định lí đảo, hệ quả
2. Phát biểu, vẽ hình, ghi giả thiết - kết luận của tính chất đường phân giác trong tam giác
hãy chỉ ra giả thiết và kết luận của định lí : hai đường thẳng phân biệt cùng song song với 1 đường thẳng thứ 3 thì chúng song song với nhau
a)vẽ hình minh họa định lí trên và viết giả thiết, kết luận bằng kí hiệu
Cho định lí:
“ Nếu hai góc đối đỉnh thì hai góc đó bằng nhau”.
a) Vẽ hình minh họa nội dung định lí trên.
b) Viết giả thiết và kết luận của định lí trên.
c) Chứng tỏ định lí trên là đúng.
a)
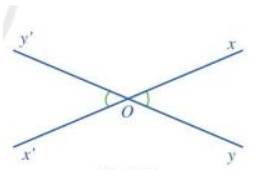
b)
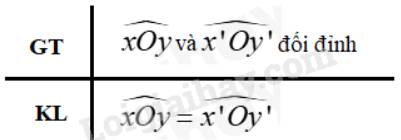
c) Vì góc xOy và x’Oy’ là hai góc đối đỉnh nên Oy và Oy’ là hai tia đối nhau; Ox và Ox’ là hai tia đối nhau
\( \Rightarrow \widehat {xOy}\) và \(\widehat {xOy'}\) là hai góc kề bù; \(\widehat {xOy'}\) và \(\widehat {x'Oy'}\) là hai góc kề bù
\( \Rightarrow \widehat {xOy} + \widehat {xOy'} = 180^\circ \); \(\widehat {xOy'} + \widehat {x'Oy'} = 180^\circ \) ( tính chất 2 góc kề bù)
\( \Rightarrow \)\(\widehat {xOy} = \widehat {x'Oy'}\) (đpcm)