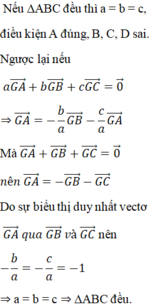Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
NB
Những câu hỏi liên quan
Nếu a,b,c là độ dài 3 cạnh của một tam giác và thỏa mãn a2+b2+c2 = ab+bc+ca thì tam giác đó là:
A. Tam giác cân
B. Tam giác vuông
C. Tam giác đều
D. Các phương án trên đều sai
Giải thích cụ thể giúp m nhé.
=> 2(a^2 + b^2 + c^2) = 2 ( ab + bc +ca)
=> 2a^2 + 2b^2 + 2c^2 - 2ab - 2bc - 2ac
=> a^2 - 2ab + b^2 + b^2 - 2bc+ c^2 + c^2 - 2ac + a^2 = 0
=> ( a- b)^2 + ( b- c)^2 + ( c -a )^2 = 0
Vì ( a- b)^2>=0 (1)
( b - c)^2 >= 0 (2)
( c -a )^2 >= 0 (3)
Từ (1)(2) và (3) => ( a- b)^2 + ( b- c)^2 + ( c -a )^2 = 0 khi
a - b = 0 và b - c = 0 và c - a = 0
=> a = b và b = c và c = a
=> a= b =c
VẬy là tam giác đều ĐÁp ấn C
Đúng 0
Bình luận (0)
a^2+b^2+c^2=ab+bc+ca=>2(a^2+b^2+c^2)=2(ab+ac+ca)
2a^2+2b^2+2c^2-2ab-2ac-2bc=0.
a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ac+c^2=0
(a-b)^2+(b-c)^2+(c-a)^2=0. => (a-b)^2=0 => a-b=0 => a=b
(b-c)^2=0 => b-c=0 => b=c
(c-a)^2=0 => c-a=0 =>c=a. Vậy a=b=c. Do đó tam giác đó là tam giác đều => C là đáp án đúng
Đúng 0
Bình luận (0)
Nếu a,b,c là độ dài 3 cạnh của một tam giác mà a2+b2+c2=ab+bc+ca thì tam giác đó là tam giác gì
tam giác đều b nhé
vì: 2a2+2b2+2c2=2ab+2ac+2bc
(a2+b2-2ab)+(a2+c2-2ac)+(b2+c2+2bc)=0
(a-b)2+(a-c)2+(b-c)2=0
a-b=0;a-c=0;b-c=0
=>a=b;a=c;b=c
vì a,b,c là 3 cạnh tam giác => a=b=c => tam giác đó là tam giác đều
Đúng 0
Bình luận (0)
Cho tam giác ABC có độ dài ba cạnh là a, b, c và ( a + b + c )^2 = 3( ab + bc + ca ). Chứng minh tam giác ABC đều.
cho tam giác ABC có độ dài ba cạnh là a,b,c sao cho a^2+b^2+c^2 = ab+bc+ca . chứng minh rằng tam giác ABC là tam giác đều
a^2+b^2+c^2=ab+bc+ac
=>2a^2+2b^2+2c^2=2ab+2bc+2ac
<=>2a^2+2b^2+2c^2-2ab-2bc-2ac=0
<=>(a^2-2ab+b^2)+(b^2-2bc+c^2)+(c^2-2ac+a^2)=0
<=>(a-b)^2+(b-c)^2+(c-a)^2=0
=>a-b=b-c=c-a=0
=>a=b;b=c;c=a
=>a=b=c
=>tam giác abc là tam giác đều
Đúng 0
Bình luận (0)
Cho tam giác ABC có 3 đường phân giác AD,BE,CF.Gọi độ dài 3 cạnh BC,CA,AB lần lượt là a,b,c.Biết a.AD +b.BE+c. CF= O.CMR tam giác ABC đều
Chứng minh rằng: nếu a, b, c là độ dài 3 cạnh của tam giác và thỏa mãn điều kiện a2 + b2+ c2 = ab + ac + bc thì tam giác đó là tam giác đều
Ta có; \(a^2+b^2+c^2=ab+bc+ca\Leftrightarrow2\left(a^2+b^2+c^2\right)=2\left(ab+bc+ca\right)\)
\(\Leftrightarrow2a^2+2b^2+2c^2=2ab+2bc+2ca\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ca=0\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ca+a^2\right)=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
Mà \(\left(a-b\right)^2\ge0;\left(b-c\right)^2\ge0;\left(c-a\right)^2\ge0\Rightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}a-b=0\\b-c=0\\c-a=0\end{cases}\Leftrightarrow a=b=c}\)
Vậy...
Đúng 0
Bình luận (0)
Tam giác ABC có trọng tâm G, độ dài các cạnh BC, CA, AB lần lượt là a, b, c. Khi đó ABC là tam giác đều nếu có điều kiện nào sau đây? A.
a
G
A
→
+
b
G
B
→
+
c
G
C
→
0...
Đọc tiếp
Tam giác ABC có trọng tâm G, độ dài các cạnh BC, CA, AB lần lượt là a, b, c. Khi đó ABC là tam giác đều nếu có điều kiện nào sau đây?
A. a G A → + b G B → + c G C → = 0 →
B. a G A → + b G B → - c G C → = 0 →
C. a G A → - b G B → + c G C → = 0 →
D. - a G A → + b G B → + c G C → = 0 →
Cho tam giác ABC có góc B = 90độ;góc C < góc A
a)Chứng minh rằng AB < BC
b)Trên cạnh BC lấy điểm D sao cho BD = BA.Chứng minh tam giác ABD là tam giác đều
c)So sánh độ dài các cạnh AB,BC,CA
Câu 1. Trong một tam giác vuông, kết luận nào sau đây là đúng ?A. Tổng hai góc nhọn bằng 180 0 B. Hai góc nhọn bằng nhauC. Hai góc nhọn phô nhau D. Hai góc nhọn kề nhau .Câu 2: Chọn câu trả lời đúng. Cho tam giác ABC có 00A50;B60 thì C?A. 70 0 B. 110 0 C. 90 0 D. 50 0Câu 3. Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:A. 1cm ; 2cm ; 3cm B. 2cm ; 3cm ; 4cmC. 3cm ; 4cm ; 5cm D. 4cm ; 5cm ; 6cmCâu 4: Chọn câu sai.A. Tam giác có hai cạnh bằng nhau là tam giác cân...
Đọc tiếp
Câu 1. Trong một tam giác vuông, kết luận nào sau đây là đúng ?
A. Tổng hai góc nhọn bằng 180 0 B. Hai góc nhọn bằng nhau
C. Hai góc nhọn phô nhau D. Hai góc nhọn kề nhau .
Câu 2: Chọn câu trả lời đúng. Cho tam giác ABC có 00
A50;B60 thì C?
A. 70 0 B. 110 0 C. 90 0 D. 50 0
Câu 3. Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:
A. 1cm ; 2cm ; 3cm B. 2cm ; 3cm ; 4cm
C. 3cm ; 4cm ; 5cm D. 4cm ; 5cm ; 6cm
Câu 4: Chọn câu sai.
A. Tam giác có hai cạnh bằng nhau là tam giác cân.
B. Tam giác có ba cạnh bằng nhau là tam giác đều.
C. Tam giác cân là tam giác đều.
D. Tam giác đều là tam giác cân.
Câu 5: Tam giác ABC vuông tại B suy ra:
A. AB 2 = BC 2 + AC 2 B. BC 2 = AB 2 + AC 2
C. AC 2 = AB 2 + BC 2 D. Cả a,b,c đều đúng
Câu 6: Hãy điền dấu X vào ô trống mà em đã chọn :
Câu Nội dung Đúng Sai
1 Tam giác vuông có một góc bằng 045 là tam giác vuông cân
2 Tam giác cân có một góc bằng 060 là tam giác đều
3 Nếu ABC là một tam giác đều thì ABC là tam giác cân
4 Nếu hai cạnh và một góc của tam giác này bằng hai cạnh và
một góc của tam giác kia thì hai tam giác đó bằng nhau
Câu 7: a). Cho ABC vuông tại A có AB = 8 cm; AC = 6 cm thì BC bằng :
A. 25 cm B. 14 cm C. 100 cm D. 10 cm
b). Cho ABC cân tại A, biết 050B thì A bằng :
A. 080 B. 050 C. 0100 D. Đáp án khác
Câu 8 . Tam giác ABC có:
A. 0ABC90 B. 0ABC180 C. 0ABC45 D. 0ABC0
Câu 9: ABC = DEF Trường hợp cạnh – góc – cạnh nếu
A. AB = DE; BF ; BC = EF B. AB = EF; BF ; BC = DF
C. AB = DE; BE ; BC = EF D. AB = DF; BE ; BC = EF
Câu 10. Góc ngoài của tam giác bằng :
A. Tổng hai góc trong không kề với nó. B. Tổng hai góc trong
C. Góc kề với nó D. Tổng ba góc trong của tam giác.
Câu 1: C
Câu 2:A
Câu 3:C
Câu 4 C
Câu 5: B
Câu 6 1Đ, 2Đ, 3Đ, 4S
Câu 7: a, Đ
Câu 10 A.
Các câu khác k rõ đề