xác định hằng số a và b sao cho
x4+ax+b chia hết cho x2-4
BN
Những câu hỏi liên quan
Xác định các hằng số a và b sao cho: x^4+4 chia hết cho x^2+ax+b
Xác định hằng số a và b sao cho ( x 4 + ax + b) ⁝ ( x 2 – 4)
A. a = 0 và b = -16
B. a = 0 và b = 16
C. a = 0 và b =0
D. a = 1 và b = 1
Ta có
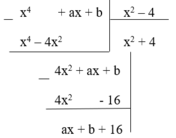
để x 4 + ax + b chia hết cho x 2 – 4 thì ax + b + 16 = 0
ó a x = 0 b + 16 = 0 ó a = 0 b = - 16
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Xác định các hằng số a và b sao cho
a) x^4 + ax + b chia hết cho x^2 - 4
b) x^4 + ax^ + bx - 1 chia hết cho x^2 - 1
c) x^3 + ax + b chia hết cho x^2 + 2x - 2
(Chia đa thức cho đa thức)
Chỉ ý kiến của mk thôi
chưa chắc đúng
Tham khảo nhé
Đúng 0
Bình luận (0)
Xác định các hằng số a và b sao cho:
a) x^4+ax+b chia hết cho x^2-4
a ) \(x^2-4=x^2-2^2=\left(x-2\right)\left(x+2\right)\)
\(f\left(x\right)=x^4+ax+b\)
Theo định lí bơ zu
\(\Rightarrow f\left(2\right)=16+2b+b=0\)
\(\Leftrightarrow2a+b=-16\) ( 1 )
\(\Rightarrow f\left(-2\right)=16-2a+b=0\)
\(\Leftrightarrow-2a+b=-16\) ( 2 )
Từ ( 1 ) và ( 2 ) \(\Leftrightarrow a=0;b=-16\)
Đúng 0
Bình luận (1)
Xác định các hằng số a và b sao cho x4+ax+b chia hết cho x2-1
Đây là phương pháp đồng nhất hạng tử (cách này hơi khó hiểu vì dành cho lớp chuyên toán hoặc đội tuyển)
sau khi lấy x4+ax+b chia cho x2-1 ta được x2+1 dư ax+b+1
ta có x4+ax+b = (x2-1)(x2+cx+d)
=>x4+ax+b=x4+cx3+dx2-x2-cx-d
Tương đương bậc của 2 bên ( ko cần ghi bậc chỉ cần ghi hệ số)
x4 =x4 => 0
0x3 =cx3 => c=0
0x2=(d-1)x2 => d-1 = 0 ( lấy x2 chung)
ax=-cx => a=-c
b=-d
Từ những điều trên ta kết luận
a=0 (a=-c mà c=0)
b=1 (b=-d mà d=1)
Đúng 0
Bình luận (0)
Xác định các hằng số a và b sao cho x4+ax+b chia hết cho x2-1
Xác định các hằng số a và b sao cho:
x4+4 chia hết cho x2+ax+b
Xác định các hằng số a và b sao cho:
x4+4 chia hết cho x2+ax+b
Áp dụng định lý Bezout hãy xác định hằng số a và b sao cho x^4 - 4 chia hết cho x^2+ax+b
Xin cảm ơn trước!!!