Bài 2: 

Nếu cả bốn góc trong một tứ giác đều là góc nhọn thì tổng của bốn góc đó sẽ nhỏ hơn 360 độ(trái với định lí tổng bốn góc trong một tứ giác)

Nếu cả bốn góc trong một tứ giác đều là góc tù thì tổng của bốn góc đó sẽ lớn hơn 360 độ(trái với định lí tổng bốn góc trong một tứ giác)

Ta có đpcm

1) Xét ΔABC và ΔCDA có 

AB=CD(gt)

\(\widehat{BAC}=\widehat{DCA}\)(hai góc so le trong, AB//CD)

AC chung

Do đó: ΔABC=ΔCDA(c-g-c)

Suy ra: \(\widehat{ACB}=\widehat{CAD}\)(hai góc tương ứng)

mà hai góc này là hai góc ở vị trí so le trong

nên AD//BC(Đpcm)

 Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn nửa chu vi tứ giác đó và nhỏ hơn chu vi tứ giác đó: 
*Theo câu 1 thì AC<p và BD < p => AC + BD < 2p tổng 2 đường chéo nhỏ hơn chu vi (đpcm) 
* giao của AC và BD là O. 
trong tam giác OAB có OB + OA > AB , trong tam giác OBC có OB + OC > BC 
trong tam giác OADcó OD + OA > AD , trong tam giác ODC có OD + OC > DC 
cổng 4 bất đẳng thức cùng chiề này lại ta có: 
2.OB + 2.OD + 2.OA + 2.OC > AB + BC + CD + DA 
<=> 2 BD + 2 AC > 2p <=> BD + AC > p tổng 2 đường chéo lớn hơn nửa chu vi (đpcm) 

Bạn tham khảo ở đây : 

/hoi-dap/question/76098.html

Gọi O là giao điểm hai đường chéo AC, BD của tứ giác ABCD.

Trong các tam giác AOB Và COD theo bất đẳng thức tam giác ta lần lượt có:

                OA + OB > AB

                OC + OD > CD.
Cộng theo từng vế hai bất đẳng thức trên ta được:

AB + BD > AB + CD

. a) Sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác OAB, OBC,OCD và ODA.

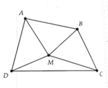
b) Chứng minh tổng hai đường chéo lớn hơn nửa chu vi tứ giác sử dụng kết quả của a).

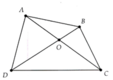
Chứng minh tổng hai đường chéo nhỏ hơn chu vi tứ giác sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác ABC, ADC, ABD và CBD

Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn nửa chu vi tứ giác đó và nhỏ hơn chu vi tứ giác đó: 
*Theo câu 1 thì AC<p và BD < p => AC + BD < 2p tổng 2 đường chéo nhỏ hơn chu vi (đpcm) 
* giao của AC và BD là O. 
trong tam giác OAB có OB + OA > AB , trong tam giác OBC có OB + OC > BC 
trong tam giác OADcó OD + OA > AD , trong tam giác ODC có OD + OC > DC 
cổng 4 bất đẳng thức cùng chiề này lại ta có: 
2.OB + 2.OD + 2.OA + 2.OC > AB + BC + CD + DA 
<=> 2 BD + 2 AC > 2p <=> BD + AC > p tổng 2 đường chéo lớn hơn nửa chu vi (đpcm) 

Gọi giao điểm của 2 đường chéo AC và BD là O .

Xét \(\Delta AOB\)có :

\(OA+OB>AB\)(1)

( Bất đẳng thức trong tam giác )

Xét \(\Delta AOD\)CÓ :

\(OC+OD>CD\)(2)

Từ (1) và (2)

\(\Rightarrow OA+OB+OC+OD>AB+CD\)

\(\Rightarrow AC+BD>AB+CD\)(đpcm)

Xét \(\Delta BOC\)có :

\(OB+OC>BC\)(1)

Xét \(\Delta AOD\)CÓ :

\(OA+OD>AD\) (2)

Từ (1) và (2)

Cộng vế với vế được :

\(OB+OC+OA+OD>BC+AD\)

\(\Rightarrow AC+BD>AD+BC\)(ĐPCM)

Vậy trong tứ giác ABCD tổng 2 đường chéo lớn hơn tổng 2 cạnh đối .