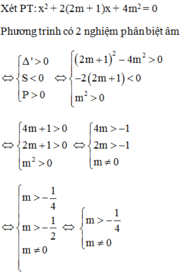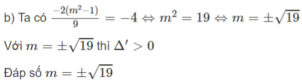Cho phương trình x2 - (2m + 1)x + m2 + m -6 = 0 . Xác định m để phương trình có nghiệm âm
NN
Những câu hỏi liên quan
Cho phương trình
x
2
– (2m – 3)x +
m
2
– 3m 0. Xác định m để phương trình có hai nghiệm
x
1
;
x
2
thỏa mãn
1
x
1
x
2
6
A. m 6 B. m 4 C.
4
≤
m...
Đọc tiếp
Cho phương trình x 2 – (2m – 3)x + m 2 – 3m = 0. Xác định m để phương trình có hai nghiệm x 1 ; x 2 thỏa mãn 1 < x 1 < x 2 < 6
A. m < 6
B. m > 4
C. 4 ≤ m ≤ 6
D. 4 < m < 6
Xét phương trình x 2 – (2m – 3)x + m 2 – 3m = 0 có a = 1 ≠ 0 và
∆ = ( 2 m – 3 ) 2 – 4 ( m 2 – 3 m ) = 9 > 0
Phương trình luôn có hai nghiệm phân biệt x 1 ; x 2
Áp dụng định lý Vi-ét ta có: x 1 + x 2 = 2 m – 3 ; x 1 . x 2 = m 2 – 3 m
Ta có 1 < x 1 < x 2 < 6
⇔ x 1 − 1 x 2 − 1 > 0 x 1 + x 2 > 1 x 1 − 6 x 2 − 6 > 0 x 1 + x 2 < 12 ⇔ x 1 x 2 − x 1 + x 2 + 1 > 0 x 1 + x 2 > 1 x 1 x 2 − 6 x 1 + x 2 + 36 > 0 x 1 + x 2 < 12 ⇔ m 2 − 3 m − 2 m + 3 + 1 > 0 2 m − 3 > 1 m 2 − 3 m − 6 2 m − 3 + 36 > 0 2 m − 3 < 12 ⇔ m 2 − 5 m + 4 > 0 2 m > 4 m 2 − 15 m + 54 > 0 2 m < 15 ⇔ m < 1 m > 4 m > 2 m < 6 m > 9 m < 15 2
⇔ 4 < m < 6
Đáp án: D
Đúng 0
Bình luận (0)
Cho phương trình:
x
2
+ 2(2m + 1)x + 4
m
2
0. Tìm m để phương trình có hai nghiệm phân biệt âm A.
m
1
4
m
≠
0
B. ...
Đọc tiếp
Cho phương trình: x 2 + 2(2m + 1)x + 4 m 2 = 0. Tìm m để phương trình có hai nghiệm phân biệt âm
A. m < 1 4 m ≠ 0
B. m > - 1 4 m ≠ 0
C. m > - 1 4
D. m > - 1 2 m ≠ 0
Cho phương trình x2 -(2m+1)x + m2 +m - 6 =0. Xác định m để phương trình có nghiệm âm
1/ Cho phương trình: 3mx^2+2(2m+1)+m=0
Xác định m để phương trình có 2 nghiệm âm
2/ Tìm m để phương trình: (m-1)x^2+2x+m=0 có ít nhất 1 nghiệm ko âm
Cho phương trình 3mx^2+2(2m+1)x+m=0. Xác định m để phương trình có 2 nghiệm âm
Cho phương trình
9
x
2
+
2
(
m
2
-
1
)
x
+
1
0
.Xác định m để phương trình có hai nghiệm
x
1
,
x
2
m
à
x...
Đọc tiếp
Cho phương trình 9 x 2 + 2 ( m 2 - 1 ) x + 1 = 0 .Xác định m để phương trình có hai nghiệm x 1 , x 2 m à x 1 + x 2 = - 4
cho phương trình x2+ 2mx -2m-6=0 (1), (với ẩn x, tham số m ). xác định giá trị của m để phương trình (1) có hai nghiệm x1,x2 sao cho x12 +x22 nhỏ nhất.
\(\Delta'=m^2+2m+6=\left(m+1\right)^2+5>0\) ;\(\forall m\Rightarrow\) pt luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=-2m-6\end{matrix}\right.\)
Đặt \(P=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(P=\left(-2m\right)^2-2\left(-2m-6\right)=4m^2+4m+12\)
\(P=\left(2m+1\right)^2+11\ge11\)
\(P_{min}=11\) khi \(m=-\dfrac{1}{2}\)
Đúng 2
Bình luận (0)
Cho phương trình
(
m
+
1
)
x
2
+
(
3
m
-
1
)
x
+
2
m
-
2
0
. Xác định m để phương trình có hai nghiệm
x
1
,
...
Đọc tiếp
Cho phương trình ( m + 1 ) x 2 + ( 3 m - 1 ) x + 2 m - 2 = 0 . Xác định m để phương trình có hai nghiệm x 1 , x 2 mà x 1 + x 2 = 3 . Tính các nghiệm trong trường hợp đó.
Với m ≠ -1
Ta có: Δ = ( m - 3 ) 2 ≥ 0 , do đó phương trình luôn luôn có hai nghiệm x 1 , x 2
Lúc đó phương trình đã cho có hai nghiệm x = -1 và x = 4.
Đúng 0
Bình luận (0)
Cho phương trình
(
m
+
2
)
x
2
+
(
2
m
+
1
)
x
+
2
0
Xác định m để phương trình có hai nghiệm trái dấu và tổng hai nghiệm bằng -3.
Đọc tiếp
Cho phương trình
( m + 2 ) x 2 + ( 2 m + 1 ) x + 2 = 0
Xác định m để phương trình có hai nghiệm trái dấu và tổng hai nghiệm bằng -3.
Phương trình có hai nghiệm trái dấu khi và chỉ khi ![]() suy ra m < -2.
suy ra m < -2.
Tổng của hai nghiệm bằng -3 khi ![]() thỏa mãn điều kiện m < -2.
thỏa mãn điều kiện m < -2.
Đáp số: m = -5.
Đúng 0
Bình luận (0)