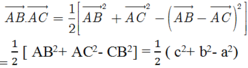Cho tam giác có AB=c, BC = a , CA=b ; ma , mb , mc là độ dài trung tuyến vẽ từ A, B, C . Cmr : \(\left(a^2+b^2+c^2\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge2\sqrt{3}\left(m_a+m_b+m_c\right)\)
NT
Những câu hỏi liên quan
Cho tam giác ABC có BC=a, AC=b, AB=c thoả mãn: ab/b+c+bc/c+a+ca/a+b=ca/b+c+ab/c+a+bc/a+b. Chứng minh tg ABC là tam giác cân
cho tam giác ABC có 3 cạnh AB,BC,CA (AB =c,BC=a,CA=b) .Gọi AM là đường trung tuyến của tam giác , Tính AM theo a,b,c
Cho tam giác ABC có BC = a, CA = b, AB = c. CMR:
ab + bc + ca ≥ 4\(\sqrt{3}\).S
Ta cần chứng minh:
\(\left(ab+bc+ca\right)^2\ge48\left(\dfrac{a+b+c}{2}\right)\left(\dfrac{a+b-c}{2}\right)\left(\dfrac{b+c-a}{2}\right)\left(\dfrac{c+a-b}{2}\right)\)
\(\Leftrightarrow\left(ab+bc+ca\right)^2\ge3\left(a+b+c\right)\left(a+b-c\right)\left(a+c-b\right)\left(b+c-a\right)\)
Mặt khác do a;b;c là 3 cạnh của 1 tam giác:
\(\Rightarrow\left(a+b-c\right)\left(a+c-b\right)\left(b+c-a\right)\le abc\)
Nên ta chỉ cần chứng minh:
\(\left(ab+bc+ca\right)^2\ge3abc\left(a+b+c\right)\) (đúng)
Đúng 1
Bình luận (1)
Ta có: \(S=\dfrac{1}{2}ab\cdot sinC=\dfrac{1}{2}bc\cdot sinA=\dfrac{1}{2}ac\cdot sinB\)
\(\Leftrightarrow\) \(ab=\dfrac{2S}{sinC}\); \(bc=\dfrac{2S}{sinA}\); \(ac=\dfrac{2S}{sinB}\)
\(\Rightarrow\) \(ab+bc+ca=2S\left(\dfrac{1}{sinA}+\dfrac{1}{sinB}+\dfrac{1}{sinC}\right)\)
Vì \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) \(\Rightarrow\) \(\dfrac{1}{sinA}+\dfrac{1}{sinB}+\dfrac{1}{sinC}\ge2\sqrt{3}\)
\(\Leftrightarrow\) \(2S\left(\dfrac{1}{sinA}+\dfrac{1}{sinB}+\dfrac{1}{sinC}\right)\ge4\sqrt{3}S\)
Hay \(ab+bc+ca\ge4\sqrt{3}S\) (đpcm)
Dấu "=" xảy ra khi \(sinA=sinB=sinC=\dfrac{\sqrt{3}}{2}\) hay \(\widehat{A}=\widehat{B}=\widehat{C}=60^o\)
hay tam giác ABC đều
Chúc bn học tốt!
Đúng 0
Bình luận (0)
Câu 12: Cho tam giác ABC có góc A bằng 450 ; góc B bằng 750. Ta có:
A. AB< BC < CA B. BC < AB < AC
C. CA < AB < BC D. CA < BC< AB
cho tam giác ABC có B=60, C<A
a,chứng minh rằng AB<BC
b,trên BC lấy D sao cho BD=BA chứng minh rằng tam giác ABD đều
c,AB,BC,CA
a) xét ΔABC ta có
C<A
=> AB < BC ( quan hệ giữa góc và cạnh đối diện trong Δ)
b)xét ΔABD ta có
BD = BA
=> ΔABD là Δ cân tại B
mà B=60o
=> ΔABD làΔ đều
Đúng 0
Bình luận (0)
Cho tam giác ABC có BC a; CA b; AB c. Tính
A
B
→
.
A
C
→
A. ½.( c2 + b2 - a2) B. c2 + b2 - a2 C. a2 - b2 - c2 D. a2 + b2 + c2
Đọc tiếp
Cho tam giác ABC có BC = a; CA = b; AB = c. Tính A B → . A C →
A. ½.( c2 + b2 - a2)
B. c2 + b2 - a2
C. a2 - b2 - c2
D. a2 + b2 + c2
Cho tam giác AB C có BC = a, CA = b, AB = c. Hãy tính \(\overrightarrow {AB} .\overrightarrow {AC} \) theo a,b,c.
Ta có: \(\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\)
Mà \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC}\)\( \Rightarrow \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \cos \widehat {BAC}\)
Lại có: \(\cos \widehat {BAC} = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)(suy ra từ định lí cosin)
\(\begin{array}{l} \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\\ \Leftrightarrow \overrightarrow {AB} .\overrightarrow {AC} = c.b.\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\\ \Leftrightarrow \overrightarrow {AB} .\overrightarrow {AC} = \frac{{{b^2} + {c^2} - {a^2}}}{2}\end{array}\)
Đúng 0
Bình luận (0)
Cho tam giác đều abc có ab=a,bc=b,ca=c chu vi tam giác đều abc là
A.C=a+b+c
B.C=a-b+c
C.C=a-b-c
D.C=a+b-c
Xem thêm câu trả lời
cho tam giác ABC vuông tại A (AB<AC) đường cao AH. Đặt BC=a, CA=b, AB=c, AH=h. cm tam giác có các cạnh a-h, b-c,h là 1 tam giác vuông
dùng Pitago đảo thử từng cặp 1 thôi:v
ta có: \(\left(b-c\right)^2+h^2=b^2+c^2-2bc+h^2\)(1)
vì tam giác ABC vuông ở A có đường cao AH nên \(a^2=b^2+c^2\)và\(AB.AB=AH.BC=2S\)hay\(b.c=a.h\)
\(\Rightarrow b^2+c^2-2bc+h^2=a^2-2ah+h^2=\left(a-h\right)^2\)
Đúng 0
Bình luận (1)
cho tam giác ABC có độ dài ba cạnh là a,b,c sao cho a^2+b^2+c^2 = ab+bc+ca . chứng minh rằng tam giác ABC là tam giác đều
a^2+b^2+c^2=ab+bc+ac
=>2a^2+2b^2+2c^2=2ab+2bc+2ac
<=>2a^2+2b^2+2c^2-2ab-2bc-2ac=0
<=>(a^2-2ab+b^2)+(b^2-2bc+c^2)+(c^2-2ac+a^2)=0
<=>(a-b)^2+(b-c)^2+(c-a)^2=0
=>a-b=b-c=c-a=0
=>a=b;b=c;c=a
=>a=b=c
=>tam giác abc là tam giác đều
Đúng 0
Bình luận (0)