Giúp em bài phần E với ạ
Em cần gấp
CT
Những câu hỏi liên quan
Giúp em bài này với ạ e cần gấp ạ:

Bài 6:
a: Xét tứ giác DEBF có
DE//BF
DE=BF
Do đó: DEBF là hình bình hành
Đúng 0
Bình luận (0)
GIÚP EM BÀI 1,PHẦN B,C BÀI 2 VỚI Ạ,EM CẦN GẤP LẮM RỒIII
GIÚP EM CÂU E BÀI 1 VỚI Ạ,EM CẦN GẤP LẮM RỒII
a: \(\left\{{}\begin{matrix}3x+6y=4\\x+4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+6y=4\\3x+12y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{3}\\x=2-\dfrac{4}{3}=\dfrac{2}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giúp e bài 2 với ạ.
Em đang cần gấp. Em cảm ơn.

Bài 2:
Xé ΔADH vuông tại H và ΔCBK vuông tại K có
AD=BC
\(\widehat{ADH}=\widehat{CBK}\)
Do đó: ΔADH=ΔCBK
Suy ra: AH=CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành
Đúng 1
Bình luận (1)
Giúp em hai bài này với ạ e cần gấp. E cảm ơn nhìu ạ
Mấy anh chị giúp em phần GTNN của các bài với ạ!! Em đang cần gấp :((

Bài 6:
a. \(A=[\frac{\sqrt{x}}{\sqrt{x}-1}+\frac{2}{\sqrt{x}(\sqrt{x}-1)}].(\sqrt{x}-1)\)
\(=\sqrt{x}+\frac{2}{\sqrt{x}}=\frac{x+2}{\sqrt{x}}\)
b. Áp dụng BĐT Cô-si cho các số dương:
$A=\sqrt{x}+\frac{2}{\sqrt{x}}\geq 2\sqrt{2}$
Vậy gtnn của $A$ là $2\sqrt{2}$. Giá trị này đạt tại $x=2$
Đúng 1
Bình luận (0)
Bài 7:
a.
\(x=\frac{1}{\sqrt{3}-1}-\frac{1}{\sqrt{3}+1}=1\)
Khi đó: \(B=\frac{1+3}{1+8}=\frac{4}{9}\)
b. \(A=\frac{(\sqrt{x}+1)(\sqrt{x}+3)+\sqrt{x}(2\sqrt{x}-1)}{(2\sqrt{x}-1)(\sqrt{x}+3)}-\frac{x+6\sqrt{x}+2}{(2\sqrt{x}-1)(\sqrt{x}+3)}\)
\(=\frac{3x+3\sqrt{x}+3-(x+6\sqrt{x}+2)}{(\sqrt{x}+3)(2\sqrt{x}-1)}=\frac{2x-3\sqrt{x}+1}{(2\sqrt{x}-1)(\sqrt{x}+3)}\)
\(=\frac{(2\sqrt{x}-1)(\sqrt{x}-1)}{(2\sqrt{x}-1)(\sqrt{x}+3)}=\frac{\sqrt{x}-1}{\sqrt{x}+3}\)
c.
\(P=AB=\frac{\sqrt{x}+3}{x+8}.\frac{\sqrt{x}-1}{\sqrt{x}+3}=\frac{\sqrt{x}-1}{x+8}\)
Áp dụng BĐT Cô-si:
$x+16\geq 8\sqrt{x}$
$\Rightarrow x+8\geq 8(\sqrt{x}-1)$
$\Rightarrow P\leq \frac{\sqrt{x}-1}{8(\sqrt{x}-1)}=\frac{1}{8}$
Vậy $P_{\max}=\frac{1}{8}$ khi $x=16$
Đúng 1
Bình luận (0)
Bài 8:
a. \(A=\frac{9+\sqrt{9}+4}{\sqrt{9}-2}=16\)
b. \(B=\frac{3x-4}{\sqrt{x}(\sqrt{x}-2)}-\frac{(\sqrt{x}+2)(\sqrt{x}-2)}{\sqrt{x}(\sqrt{x}-2)}-\frac{\sqrt{x}(\sqrt{x}-1)}{\sqrt{x}(\sqrt{x}-2)}\)
\(=\frac{3x-4-(x-4)-(x-\sqrt{x})}{\sqrt{x}(\sqrt{x}-2)}=\frac{x+\sqrt{x}}{\sqrt{x}(\sqrt{x}-2)}=\frac{\sqrt{x}+1}{\sqrt{x}-2}\) (đpcm)
c. Áp dụng BĐT Cô-si:
\(P=A:B=\frac{x+\sqrt{x}+4}{\sqrt{x}-2}:\frac{\sqrt{x}+1}{\sqrt{x}-2}=\frac{x+\sqrt{x}+4}{\sqrt{x}+1}\)
\(=\sqrt{x}+\frac{4}{\sqrt{x}+1}=(\sqrt{x}+1)+\frac{4}{\sqrt{x}+1}-1\geq 2\sqrt{4}-1=3\)
Vậy $P_{\min}=3$ khi $x=1$
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Làm giúp e bài này với. Em cần gấp ạ
Mọi người ơi giúp em giải bài này với em cần gấp lắm, em cảm ơn trc vì đã giúp e ạ!!
ai giúp em làm bài 3 nhanh với đầy đủ giùm em ạ, e cần gấp:((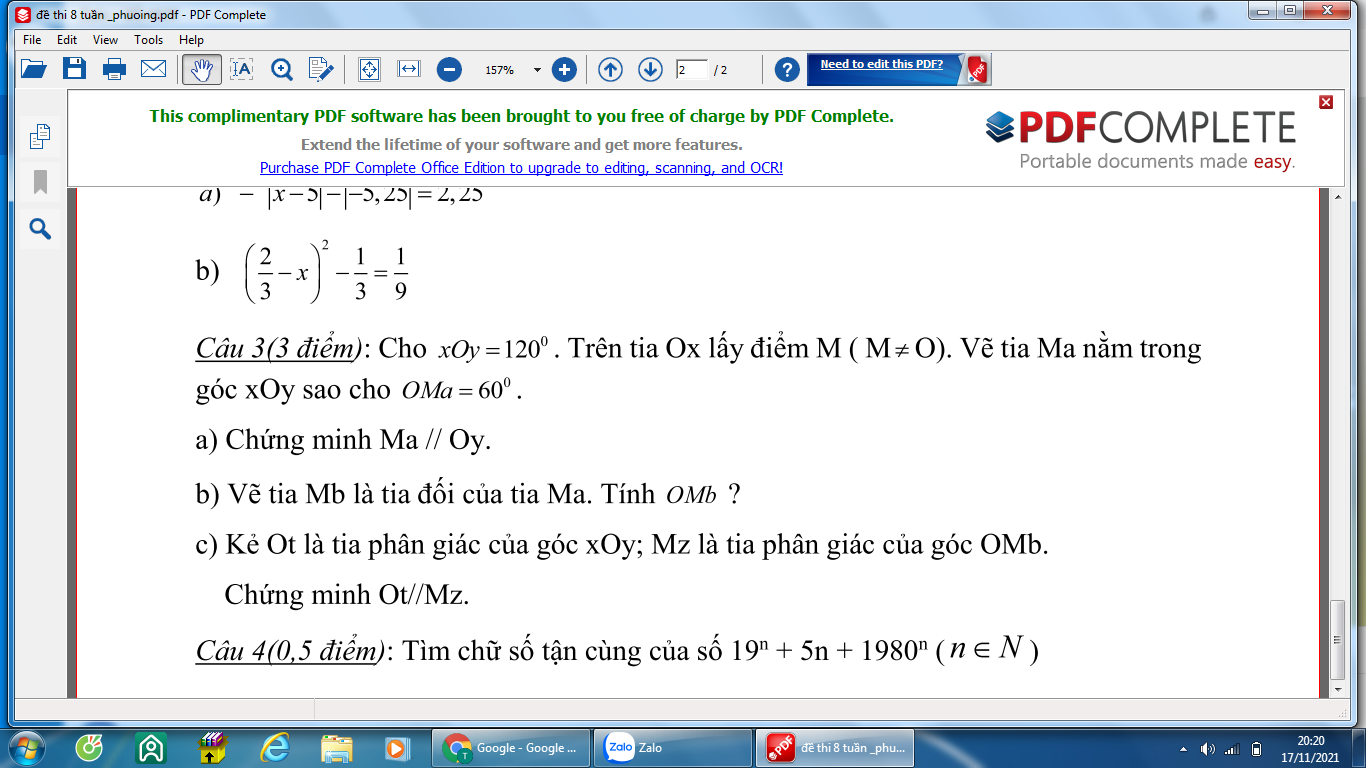
Bài nào, bạn ghi rõ ra mình mới biết nha
Đúng 0
Bình luận (0)





