Cho em xin các công thức tính nhanh bán kính ngoại tiếp mặt cầu với ạ
MM
Những câu hỏi liên quan
Cho
A
1
;
1
;
0
;
B
-
1
;
1
;
0
;
C
1
;
-
1
;
0
;
D...
Đọc tiếp
Cho A 1 ; 1 ; 0 ; B - 1 ; 1 ; 0 ; C 1 ; - 1 ; 0 ; D - 1 ; - 1 ; 0 là tâm của 4 mặt cầu có bán kính bằng 1. Gọi I là tâm mặt cầu (S) có bán kính bằng 1 tiếp xúc ngoài với cả 4 mặt cầu kể trên. Tính bán kính R của mặt cầu ngoại tiếp hình chóp I.ABCD.
![]()
![]()
![]()
![]()
Giúp em với ạ Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SA=2a. Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD là A.3a B.a căn3/6 C.a căn6/2 D.a căn8/3
Cho tứ diện ABCD có các mặt ABC và BCD là các tam giác đều cạnh 2, hai mặt phẳng (ABD) và (ACD) vuông góc với nhau. Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD. A.
2
2
B.
2
C.
2
3
3
D.
6
3
Đọc tiếp
Cho tứ diện ABCD có các mặt ABC và BCD là các tam giác đều cạnh 2, hai mặt phẳng (ABD) và (ACD) vuông góc với nhau. Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD.
A. 2 2
B. 2
C. 2 3 3
D. 6 3
Chọn B.
Phương pháp:
Ta xác định tâm mặt cầu ngoại tiếp tứ diện ABCD chính là điểm cách đều bốn đỉnh A, B, C, D.
Dựa vào tính chất tam giác cân, hai tam giác bằng nhau, tỉ số lượng giác để chứng minh các đoạn thẳng bằng nhau từ đó tìm được tâm mặt cầu.
Cách giải:
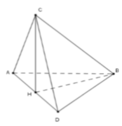
Các tam giác đều ABC và BCD có cạnh 2
⇒ B D = D C = B C = A B = A C = 2
Nên tam giác CAD cân tại C và tam giác BAD cân tại B.

Từ (1) và (2) suy ra tam giác CHB vuông cân tại H có cạnh huyền CB = 2.

Đúng 0
Bình luận (0)
Cho một hình lập phương có bán kính mặt cầu ngoại tiếp, mặt cầu nội tiếp và mặt cầu tiếp xúc với tất cả các cạnh của hình lập phương lần lượt là
R
1
,
R
2
,
R
3
. Mệnh đề nào sau đây đúng? A.
R
1
R
3
R
2
B. ...
Đọc tiếp
Cho một hình lập phương có bán kính mặt cầu ngoại tiếp, mặt cầu nội tiếp và mặt cầu tiếp xúc với tất cả các cạnh của hình lập phương lần lượt là R 1 , R 2 , R 3 . Mệnh đề nào sau đây đúng?
A. R 1 > R 3 > R 2
B. R 1 > R 2 > R 3
C. R 3 > R 1 > R 2
D. R 2 > R 1 > R 3
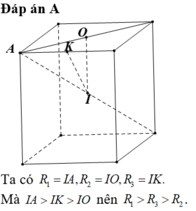
Đáp án A
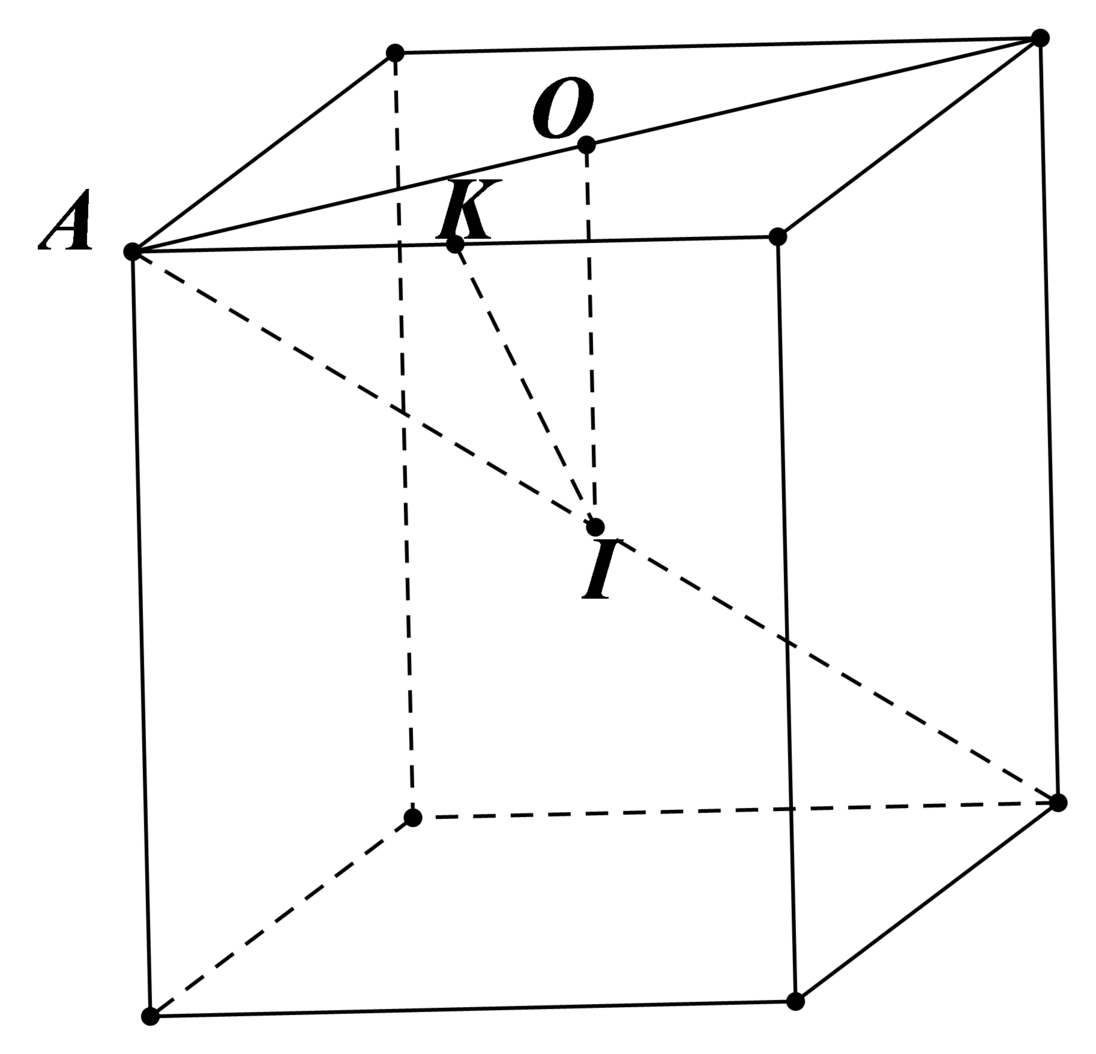
Ta có: R 1 = I A , R 2 = I O , R 3 = I K . Mà I A > I K > I O nên R 1 > R 3 > R 2 .
Đúng 0
Bình luận (0)
Cho một hình lập phương có bán kính mặt cầu ngoại tiếp, mặt cầu nội tiếp và mặt cầu tiếp xúc với tất cả các cạnh của hình lập phương lần lượt là
R
1
,
R
2
,
R
3
. Mệnh đề nào sau đây đúng?
Đọc tiếp
Cho một hình lập phương có bán kính mặt cầu ngoại tiếp, mặt cầu nội tiếp và mặt cầu tiếp xúc với tất cả các cạnh của hình lập phương lần lượt là R 1 , R 2 , R 3 . Mệnh đề nào sau đây đúng?
![]()
![]()
![]()
![]()
Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD với AB=2a
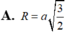
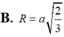
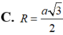
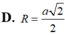
Cho khối chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và SA a Đáy ABC nội tiếp trong đường tròn tâm I có bán kính bằng 2a (tham khảo hình vẽ). Tính bán kính mặt cầu ngoại tiếp khối chóp S.ABC A.
a
5
2
B.
a
17
2
C.
a...
Đọc tiếp
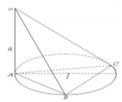
Cho khối chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và SA = a Đáy ABC nội tiếp trong đường tròn tâm I có bán kính bằng 2a (tham khảo hình vẽ). Tính bán kính mặt cầu ngoại tiếp khối chóp S.ABC
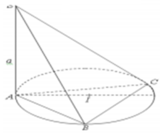
A. a 5 2
B. a 17 2
C. a 5
D. a 5 3
Đáp án B
Qua I dựng đường thẳng d song song với SA (vuông góc với mặt phẳng (ABC)). Mặt phẳng trung trực của SA cắt d tại tâm mặt cầu ngoại tiếp tam giác ABC.
Bán kính mặt cầu là R = 4 a 2 + a 2 4 = a 17 2
Đúng 0
Bình luận (0)
Cho khối chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và SAa. Đáy ABC nội tiếp trong đường tròn tâm I có bán kính bằng 2a (tham khảo hình vẽ). Tính bán kính mặt cầu ngoại tiếp khối chóp S.ABC
Đọc tiếp
Cho khối chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và SA=a. Đáy ABC nội tiếp trong đường tròn tâm I có bán kính bằng 2a (tham khảo hình vẽ). Tính bán kính mặt cầu ngoại tiếp khối chóp S.ABC
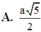
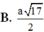
![]()
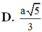
Cho khối chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và SA a. Đáy ABC nội tiếp trong đường tròn tâm I có bán kính bằng 2a (tham khảo hình vẽ). Tính bán kính mặt cầu ngoại tiếp khối chóp S.ABC A.
a
5
2
B.
a
17
2
C.
a
5
D.
a
17
Đọc tiếp
Cho khối chóp S.ABC có SA vuông góc với mặt phẳng
(ABC) và SA = a. Đáy ABC nội tiếp trong đường tròn
tâm I có bán kính bằng 2a (tham khảo hình vẽ). Tính
bán kính mặt cầu ngoại tiếp khối chóp S.ABC
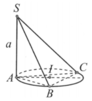
A. a 5 2
B. a 17 2
C. a 5
D. a 17