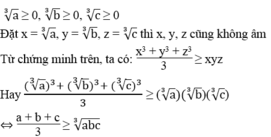Chứng minh các bất đẳng thức sau:
a/ Nếu x2 + y2 = u2 + v2 thì |x(u+v) + y(u-v)| \(x <= \sqrt{2}\)
Chứng minh các bất đẳng thức sau:
a/ Nếu x2 + y2 = u2 + v2 thì |x(u+v) + y(u-v)| <=√2
\(\left|x\left(u+v\right)-y\left(u-v\right)\right|^2\le\left(x^2+y^2\right)\left[\left(u+v\right)^2+\left(u-v\right)^2\right]=1\cdot\left(2u^2+2v^2\right)=2\)
\(\Rightarrow\left|x\left(u+v\right)-y\left(u-v\right)\right|\le\sqrt{2}\)
@Hải Ngọc Cảm ơn câu trả lời của bạn, nhưng ở đoạn đầu bạn nhầm dấu cộng thành dấu trừ rồi! :))
Chứng minh các bất đẳng thức sau với x, y, z > 0
a) x2 + y2 ≥ (x + y)2/2
b) x3 + y3 ≥ (x + y)3/4
c) x4 + y4 ≥ (x + y)4/8
d) x2 + y2 + z2 ≥ xy + yz + zx
e) x2 + y2 + z2 ≥ (x + y + z)2/3
f) x3 + y3 + z3 ≥ 3xyz
a: Ta có: \(\left(x+y\right)^2\)
\(=x^2+2xy+y^2\)
\(\Leftrightarrow x^2+y^2=\dfrac{\left(x+y\right)^2}{2xy}\ge\dfrac{\left(x+y\right)^2}{2}\forall x,y>0\)
Chứng minh các đẳng thức sau:
a) − u 2 + 3 u − 2 ( u + 2 ) ( u − 1 ) = u 2 − 4 u + 4 4 − u 2 với u ≠ ± 2 và u ≠ 1 ;
b) v 3 + 27 v 2 − 3 v + 9 = v + 3 .
Chứng minh đẳng thức: u − uv + v − v 2 v 3 − 3 v 2 + 3 v − 1 = u + v − v 2 + 2 v − 1 với v ≠ 1 .
Gợi ý: u – uv + v – v 2 = (1 – v)(u + z).
chứng minh các đẳng thức sau
(x+y)2+(x-y)2=2(x2+y2)
\(\left(x+y\right)^2+\left(x-y\right)^2=2\left(x^2+y^2\right)\)
\(\Leftrightarrow x^2+2xy+y^2+x^2-2xy=2\left(x^2+y^2\right)\)
\(\Leftrightarrow2x^2+2y^2=2\left(x^2+y^2\right)\left(đúng\right)\)
chứng minh các đẳng thức sau
(x+y)2+(x-y)2=2(x2+y2)
chứng minh bất đẳng thức\(\frac{\text{(x2+y2)2 }}{\left(x-y\right)^2}\)>=8
CMR : a) Có thể tìm được số có dạng 199119911991...19910...0 chia hết cho 1992
Help
Chứng minh các đẳng thức sau: - x 2 + 2 x y - y 2 x 2 - y 2 = - x + y x + y
Chứng minh: x 3 + y 3 + z 3 - 3 x y z = 1 / 2 . x + y + z x - y 2 + y - z 2 + z - x 2
Từ đó chứng tỏ: Với ba số a, b, c không âm thì x 3 + y 3 + z 3 3 ≥ x y z
(Bất đẳng thức Cô-si cho ba số không âm)
Dấu đẳng thức xảy ra khi ba số a, b, c bằng nhau.
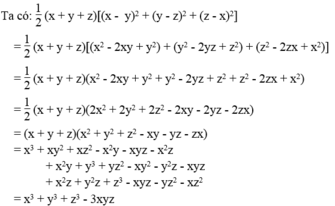
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Nếu a ≥ 0, b ≥ 0, c ≥ 0 thì :