NM
Những câu hỏi liên quan
Cho tam giác ABC vuông ở A, đường cao AH. Hệ thức nào sai?`AB^2 BH.BC``AH^2 BH.CH``(AH)/(AC) (AB)/(BC)``(AH)/(BH) (AB)/(AC)`Cho tam giác `ABC` có `AB3;AC4;BC5`, đường cao `AH`. Hệ thức nào sai?`AH^2 BH.CH``BH^2 AH.CH``AB^2 BH.BC``1/(AB^2) 1/(AH^2) - 1/(AC^2)`Cho tam giác ABC vuông ở `B`, đường cao `BH`. Hệ thức nào đúng?`BH^2 AH.CH``AH^2 BH.CH``AB^2 BH.BC``AB^2 +AC^2 BC^2`
Đọc tiếp
Cho tam giác ABC vuông ở A, đường cao AH. Hệ thức nào sai?
`AB^2 = BH.BC`
`AH^2 = BH.CH`
`(AH)/(AC) = (AB)/(BC)`
`(AH)/(BH) = (AB)/(AC)`
Cho tam giác `ABC` có `AB=3;AC=4;BC=5`, đường cao `AH`. Hệ thức nào sai?
`AH^2 = BH.CH`
`BH^2 = AH.CH`
`AB^2 = BH.BC`
`1/(AB^2) = 1/(AH^2) - 1/(AC^2)`
Cho tam giác ABC vuông ở `B`, đường cao `BH`. Hệ thức nào đúng?
`BH^2 = AH.CH`
`AH^2 = BH.CH`
`AB^2 = BH.BC`
`AB^2 +AC^2 = BC^2`
Câu 1: D
Câu 2: B
Câu 3: A
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH.
CMR: AB2= BH.BC
Xét tam giác ABH và tam giác ABC có
góc AHB = góc BAC (= 90 độ)
góc BAH = góc C (cùng phụ góc B)
\(\Rightarrow\) tam giác HAB đồng dạng với tam giác ACB
\(\Rightarrow\frac{AB}{BC}=\frac{BH}{AB}\Rightarrow AB^2=BH\cdot BC\)
Đúng 0
Bình luận (0)
Xét tam giác ABH và tam giác CBA có:
góc B chung
góc AHB = góc CAB ( = 900)
=> 2 tam giác đồng dạng
\(\Rightarrow\frac{AB}{BC}=\frac{BH}{AB}\Rightarrow AB^2=BH.BC\)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A có AB=3cm, BC=5cm, vẽ đường cao AH của tam giác ABC
a)CM tam giác ABC đồng dạng với tam giác HBA
b)CMR AB^2 = BH.BC. tính BH
c)Dựng đường phân giác BD của tam giác ABC cắt AH ở E. Tính EH/EA. tính EH .
d) tính diện tích tứ giác HEDC
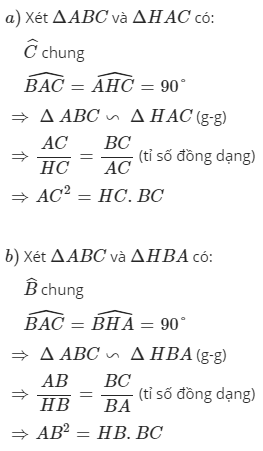

Mik copy trên mạng nên cs chút sai sót thì mog bn bỏ qua =)
Đúng 0
Bình luận (0)
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABH}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
b: Ta có: ΔABC\(\sim\)ΔHBA
nên \(\dfrac{AB}{HB}=\dfrac{CB}{AB}\)
hay \(AB^2=BH\cdot BC\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ HM vuông góc AB, HN vuông góc AC. CMR;
a) AN.AC=HB.HC
b) AB²/AC²=BH/HC
c) AH²+BH²=BH.BC
b: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\)
hay \(\dfrac{AB^2}{AC^2}=\dfrac{BH}{CH}\)
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A. có AB=6cm, AC=8cm, BC=10cm. vẽ đường cao AH
a) cmr tam giác ABC đồng dạng với tam giác AHB
b) cmr AB2=BH.BC. tính BH,HC
c) vẽ phân giác AD của góc A (A thuộc BC). tính DB
Tam giác `ABC` có đường AH thỏa mãn `AH^2 = CH.BH` thì khẳng định nào đúng?
`\triangle ABC` vuông ở `A`
`AB^2 = BH.BC`
`\triangle AHB` đồng dạng `\triangle CHA`
`AB^2 +AC^2 = BC^2`
Cho tam giác ABC vuông ở `A,AB=3;AC=4`. Đường cao `AH`. Tính `AH`?
Câu 1: Cả 4 câu đều đúng
Câu 2:
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=3^2+4^2=25\)
=>BC=5
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot5=3\cdot4=12\)
=>AH=2,4
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A, đường cao AH. Chứng minh rằng:a) Tam giác ABC đồng dạng với tam giác HBA;b) AB BH.BC 2 ;c) AH BH.HC 2 .
Đọc tiếp
Cho tam giác ABC vuông ở A, đường cao AH. Chứng minh rằng:
a) Tam giác ABC đồng dạng với tam giác HBA;
b) AB BH.BC 2 ;
c) AH BH.HC 2 .
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: ΔBAC đồng dạng với ΔBHA
=>BA/BH=BC/BA
=>BA^2=BH*BC
c: Xét ΔHAC vuông tại H và ΔHBA vuông tại H có
góc HAC=góc HBA
=>ΔHAC đồng dạng với ΔHBA
=>HA/HB=HC/HA
=>HA^2=HB*HC
Đúng 0
Bình luận (1)
cho tam giác ABC vuông tại A, đường cao AH. chứng minh \(AB^2\)= BH.BC (Bằng cách sử dụng tỉ số lượng giác của góc nhọn)
Cho tam giác ABC vuông tại A có AB=3cm, BC=5cm, vẽ đường cao AH của tam giác ABC.
a) CM: tam giác ABC~ tam giác HBA
b) CM: AB^2=BH.BC, tính BH
c) Dựng đường p/g BD của tam giác ABC cắt AH ở E. Tính EH/EA. Tính EH
d) Tính diện tích tứ giác HEDC
a: XétΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó:ΔABC\(\sim\)ΔHBA
b: Ta có: ΔABC\(\sim\)ΔHBA
nên BA/BH=BC/BA
hay \(BA^2=BH\cdot BC\)
\(BH=\dfrac{BA^2}{BC}=\dfrac{3^2}{5}=1.8\left(cm\right)\)
Đúng 0
Bình luận (0)


