cho tam giác ABC đường cao AH lấy D sao cho B nằm giữa Dvà C so sánh AD và AB so sánh ADB và ACB
H24
Những câu hỏi liên quan
1. Cho tam giác ABC có AB < AC, có AD là đường phân giác. Trên cạnh AC lấy E sao cho AE = AB. So sánh tam giác ADB và tam giác AED.
2. Trên cạnh Ax và Ay của xAy, lần lượt lấy các điểm B và C sao cho AB = AC. Tia phân giác At của xAy cắt BC tại D. So sánh tam giác ADB và tam giác CDA và so sánh các cặp cạnh và góc tương ứng giữa chúng.
Giúp mk vs huuhu
Bài 2.Cho tam giác ABC nhọn, điểm D nằm giữa B và C sao cho AD không vuông góc với BC. Gọi H và K là chân đường vuông góc kẻ từ B và C đến đường thẳng AD.
a) So sánh BH+CKvà AB+AC
b) So sánh BH+CKvới BC
a: ΔBHA vuông tại H
=>BH<AB
ΔCKA vuông tại K
=>CK<AC
=>BH+CK<AB+AC
b: ΔBDH vuông tại H
=>BH<BD
ΔCKD vuông tại K
=>CK<CD
=>BH+CK<BD+CD=BC
Đúng 0
Bình luận (0)
Cho tam giác ABC ,AB=AC đường cao AH lấy D sao cho B nằm giữa D và C
a, So sánh AD và AB
b, So sánh góc ADB và góc ACB
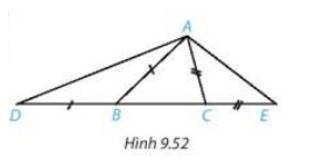
Cho tam giác ABC ( AB > AC). Trên đường thẳng chứa cạnh BC, lấy điểm D và điểm E sao cho B nằm giữa D và C, C nằm giữa B và E, BD = BA, CE = CA ( H.9.52)
a) So sánh \(\widehat {ADE}\) và \(\widehat {AED}\).
b) So sánh các đoạn thẳng AD và AE.
a)
\(AB > AC \Rightarrow \widehat {ABC} < \widehat {ACB}\)( quan hệ giữa góc và cạnh đối diện trong tam giác ABC)
\(\begin{array}{l} \Rightarrow {180^0} - \widehat {ABD} < {180^0} - \widehat {ACE}\\ \Rightarrow \widehat {ABD} > \widehat {ACE}\end{array}\)
Vì BD= BA nên tam giác ABD cân tại B \( \Rightarrow \widehat {ABD} = {180^0} - 2\widehat {ADB}\)
Vì CE = CA nên tam giác ACE cân tại C \( \Rightarrow \widehat {ACE} = {180^0} - 2\widehat {AEC}\)
\(\begin{array}{*{20}{l}}{ \Rightarrow {{180}^0} - 2\widehat {ADB} > {{180}^0} - 2\widehat {AEC}}\\{ \Rightarrow \widehat {ADB} < \widehat {AEC}}\\{Hay{\mkern 1mu} \widehat {ADE} < \widehat {AED}}\end{array}\)
b) Xét tam giác ADE ta có : \(\widehat {ADB} < \widehat {AEC}\)
\( \Rightarrow AD > AE\)(Quan hệ giữa cạnh và góc đối diện trong tam giác).
Đúng 0
Bình luận (0)
Bài 2: Cho tam giác ABC (AB<AC). Trên tia đối của tia BC lấy điểm D sao cho BD=AB. Trên tia đối của tia CB lấy điểm E sao cho CE=AC. Vẽ các đoạn thẳng AD, AE
a, Chứng minh: Góc CAE = góc AEC
b, Hãy so sánh: Góc ABC và góc ACB
c, Vẽ đường cao AH. So sánh HD và HE
a, vì CA=CE(GT) =>TAM GIÁC ACE CÂN TẠI C=> GÓC CAE= GÓC AEC
b,vì AB<AC=>góc ABC>góc ACB(quan hệ giữa góc và cạnh trong 1 tam giác)
c, vì AH là đường cao => AH là đường vuông góc
TA CÓ AB=BD, AC=CE MÀ AB<AC=>BD<CE=>HD<HE(quan hệ giữa đx và hc)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A,đường cao AH và góc B = 60 độ. Trên tia đối của HA lấy điểm D sao cho H là trung điểm của AD
a) so sánh AB và AC
b) chứng minh: △AHC=△DHC
c) chứng minh: BC là đường trung trực của AD
a: góc C=90-60=30 độ
góc B>góc C
=>AC>AB
b: Xét ΔAHC vuông tại H và ΔDHC vuông tại H có
HC chung
HA=HD
=>ΔAHC=ΔDHC
c: ΔAHC=ΔDHC
=>CA=CD
mà HA=HD
nên CH là trung trực của AD
=>BC là trung trực của AD
Đúng 1
Bình luận (0)
CHO TAM GIÁC ABC VUÔNG TẠI A CÓ GÓC C=30 . KẺ AH VUÔNG GÓC BC. TRÊN ĐOẠN THẲNG HC LẤY D SAO CHO HD=HB. E LÀ CHÂN ĐƯỜNG VUÔNG GÓC KẺ TỪ C ĐẾN AD
. CHỨNG MINH
A, , AB=AD
B, TAM GIÁC ABD ĐỀU
C, SO SÁNH AH VÀ CE
D, BIẾT AB=5CM. TÍNH ĐỘ DÀI AH VÀ BC
a: Xét ΔABD có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔABD cân tại A
=>AB=AD
b: Ta có: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}+30^0=90^0\)
=>\(\widehat{ABC}=60^0\)
Xét ΔABD cân tại A có \(\widehat{ABD}=60^0\)
nên ΔABD đều
c: Ta có: ΔABD đều
=>\(\widehat{BAD}=60^0\)
Ta có: \(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}\)
=>\(\widehat{CAD}=90^0-60^0=30^0\)
Xét ΔDAC có \(\widehat{DAC}=\widehat{DCA}\left(=30^0\right)\)
nên ΔDAC cân tại D
=>DA=DC
Xét ΔDHA vuông tại H và ΔDEC vuông tại E có
DA=DC
\(\widehat{ADH}=\widehat{CDE}\)(hai góc đối đỉnh)
Do đó: ΔDHA=ΔDEC
=>AH=EC
d: Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}\)
=>\(\dfrac{5}{BC}=sin30=\dfrac{1}{2}\)
=>\(BC=5\cdot2=10\left(cm\right)\)
Xét ΔAHB vuông tại H có \(sinB=\dfrac{AH}{AB}\)
=>\(\dfrac{AH}{5}=sin60=\dfrac{\sqrt{3}}{2}\)
=>\(AH=\dfrac{5\sqrt{3}}{2}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC (AC > AB), trung tuyến AM. Trên tia đối của tia MA lấy D sao cho MD = MA.
c. Kẻ đường cao AH. Lấy E là một điểm nằm giữa A và H. So sánh độ dài HC và HB, EB và EC.

c. Vì AB < AC ⇒ HB < HC (quan hệ giữa hình chiếu và đường xiên) (1 điểm)
Vì HB < HC ⇒ BE < EC (quan hệ giữa hình chiếu và đường xiên) (1 điểm)
Đúng 0
Bình luận (0)
cho tam giac ABC nhọn,AB>AC. kẻ AH vuông góc BC (H thuộc BC). trên tia đối của tia BC lấy điểm D sao cho BD=AB.trên tia đối của CB lấy điểm E sao cho CE=AC.
a)so sánh góc ABC và ACB.
b)so sánh hai góc ADB và AEC.
c)so sánh HD và HE


