Tính diện tích lối vào (S1) và diện tích phòng chính (S2) của một căn hộ có sơ đồ như sau:
Đọc tiếp
Tính diện tích lối vào (S1) và diện tích phòng chính (S2) của một căn hộ có sơ đồ như sau:
NH
Những câu hỏi liên quan
H24
SGK Chân trời sáng tạo
22 tháng 7 2023 lúc 8:17
a) Hình 3a là bản vẽ sơ lược sàn của một căn hộ (các kích thước tính theo m). Tính diện tích sàn này bằng những cách khác nhau.
b) Nếu vẽ cả ban công thì được sơ đồ như Hình 3b. Hãy tính tổng diện tích của sàn bao gồm cả ban công.
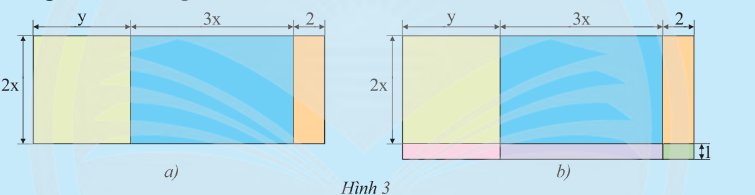
a) Cách 1: Diện tích sàn là: \(2x.\left( {y + 3x + 2} \right) = 2x.y + 2x.3x + 2x.2 = 2xy + 6{x^2} + 4x\)
Cách 2: Diện tích sàn là: \(2x.y + 2x.3x + 2x.2 = 2xy + 6{x^2} + 4x\)
b) Diện tích ban công là: \(1.\left( {y + 3x + 2} \right) = y + 3x + 2\)
Tổng diện tích sàn bao gồm cả ban công là: \(\left( {2xy + 6{x^2} + 4x} \right) + \left( {y + 3x + 2} \right) = 2xy + 6{x^2} + 4x + y + 3x + 2 = 2xy + 6{x^2} + y + 7x + 2\)
Đúng 0
Bình luận (0)
Có thể xác định diện tích một căn phòng bằng 2 cách: đo chiều dài và chiều rộng, hoặc đếm các viên gạch theo chiều dài và chiều rộng, rồi tính ra diện tích.a. Cách nào chính xác hơn? Vì sao?b. Để chuẩn bị kê giường, tủ vào một căn phòng, người ta thường chỉ dùng phương pháp đếm gạch. Vì sao?Có thể xác định diện tích một căn phòng bằng 2 cách: đo chiều dài và chiều rộng, hoặc đếm các viên gạch theo chiều dài và chiều rộng, rồi tính ra diện tích.a. Cách nào chính xác hơn? Vì sao?b. Để chuẩn bị kê...
Đọc tiếp
Có thể xác định diện tích một căn phòng bằng 2 cách: đo chiều dài và chiều rộng, hoặc đếm các viên gạch theo chiều dài và chiều rộng, rồi tính ra diện tích.
a. Cách nào chính xác hơn? Vì sao?
b. Để chuẩn bị kê giường, tủ vào một căn phòng, người ta thường chỉ dùng phương pháp đếm gạch. Vì sao?
Có thể xác định diện tích một căn phòng bằng 2 cách: đo chiều dài và chiều rộng, hoặc đếm các viên gạch theo chiều dài và chiều rộng, rồi tính ra diện tích.
a. Cách nào chính xác hơn? Vì sao?
b. Để chuẩn bị kê giường, tủ vào một căn phòng, người ta thường chỉ dùng phương pháp đếm gạch. Vì sao?
Có thể xác định diện tích một căn phòng bằng 2 cách: đo chiều dài và chiều rộng, hoặc đếm các viên gạch theo chiều dài và chiều rộng, rồi tính ra diện tích.
a. Cách nào chính xác hơn? Vì sao?
b. Để chuẩn bị kê giường, tủ vào một căn phòng, người ta thường chỉ dùng phương pháp đếm gạch. Vì sao?
Một hình vuông ABCD có cạnh
A
B
a
, diện tích
S
1
. Nối 4 trung điểm
A
1
,
B
1
,
C
1
,
D
1
theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai là
A
1
B
1...
Đọc tiếp
Một hình vuông ABCD có cạnh A B = a , diện tích S 1 . Nối 4 trung điểm A 1 , B 1 , C 1 , D 1 theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai là A 1 B 1 C 1 D 1 có diện tích S 2 . Tiếp tục như thế ta được hình vuông thứ ba là A 2 B 2 C 2 D 2 có diện tích S 3 và cứ tiếp tục như thế, ta được diện tích S 4 , S 5 , . . .
Tính S = S 1 + S 2 + S 3 + . . . . + S 100
A. S = 2 100 - 1 2 99 a 2
B. S = a 2 100 - 1 2 99
C. S = a 2 2 100 - 1 2 99
D. S = a 2 2 99 - 1 2 99
Ta tính được
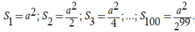
Như vậy
S
1
,
S
2
,
S
3
,
.
.
.
,
S
100
là cấp số nhân với 
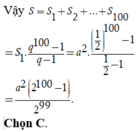
Đúng 0
Bình luận (0)
Một hình vuông ABCD có ạnh ABa, diện tích
S
1
. Nối bốn trung điểm
A
1
,
B
1
,
C
1
,
D
1
theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai
A
1
B
1
C
1...
Đọc tiếp
Một hình vuông ABCD có ạnh AB=a, diện tích S 1 . Nối bốn trung điểm A 1 , B 1 , C 1 , D 1 theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai A 1 B 1 C 1 D 1 có diện tích S 2 . Tiếp tục như thế ta được hình vuông thứ ba A 2 B 2 C 2 D 2 có diện tích S 3 và cứ tiếp tục như thế ta được diện tíc thứ S 4 , S 5 , ... Tính T= S 1 + S 2 + S 3 + . . . + S 1 00
A. S = 2 100 - 1 2 99 a 2
B. S = a 2 100 - 1 2 99
C. S = a 2 2 100 - 1 2 99
D. S = a 2 2 99 - 1 2 99
Để lát một căn phòng cần dùng 120 viên gạch hình chữ nhật có chiều rộng là 20cm, chiều dài là 30cm. Tính diện tích của căn phòng đó ( diện tích căn phòng chính là tổng diện tích của 120 viên gạch)
ai giúp mình với
Diện tích phòng là \(20\times30\times120=72000\left(cm^2\right)\)
Đúng 3
Bình luận (1)
Diện tích của một viên gạch là:
20.30=600(cm)
Diện tích của căn phòng đó là:
600.120=72 000(cm)
Đáp số:72 000cm
Đúng 2
Bình luận (3)
diện tích 1 viên gạch là:
30.20=600(cm2)
diện tích của căn phòng là:
120.600=72000(cm2)
đáp số: 7200cm2
Đúng 0
Bình luận (0)
Dùng một lực F1 để tác dụng vào píttông có diện tích S1 của một máy nén dùng chất lỏng. Nếu tăng F1 lên hai lần và giảm diện tích S1 đi hai lần thì lực tác dụng vào píttông có diện tích S2 sẽ A. tăng lên 4 lần B. tăng lên hai lần C. tăng lên tám lần D. không thay đổi
Đọc tiếp
Dùng một lực F1 để tác dụng vào píttông có diện tích S1 của một máy nén dùng chất lỏng. Nếu tăng F1 lên hai lần và giảm diện tích S1 đi hai lần thì lực tác dụng vào píttông có diện tích S2 sẽ
A. tăng lên 4 lần
B. tăng lên hai lần
C. tăng lên tám lần
D. không thay đổi
Đáp án: A
Máy nén thủy lực hoạt động dựa vào nguyên lí Pa-xcan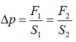 
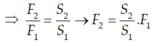
Đúng 0
Bình luận (0)
Một hình vuông
A
B
C
D
có cạnh
A
B
a
.
, diện tích
S
1
.
Nối 4 trung điểm
A
1
,
B
1
,
C
1
,
D
1
theo thứ tự của 4 cạnh
A
B
,
B
C
,...
Đọc tiếp
Một hình vuông A B C D có cạnh A B = a . , diện tích S 1 . Nối 4 trung điểm A 1 , B 1 , C 1 , D 1 theo thứ tự của 4 cạnh A B , B C , C D , D A ta được một hình vuông thứ hai A 1 , B 1 , C 1 , D 1 có diện tích S 2 . Tiếp tục như vậy ta được hình vuông thứ 3 là có diện tích S 3 và cứ như thế ta được S 4 , S 5 ,... Tính giá trị của S = S 1 + S 2 + S 3 + ... + S 100
A. 2 100 − 1 2 99 a 2
B. a 2 100 − 1 2 99
C. a 2 2 100 − 1 2 99
D. a 2 2 99 − 1 2 99
Đáp án C
Diện tích hình vuông A B C D là S 1 = a 2 ; diện tích hình vuông A 1 B 1 C 1 D 1 là S 2 = a 2 2 2 = a 2 2
Diện tích hình vuông A 2 B 2 C 2 D 2 là a 2 2 = a 2 4 ; ...
Diện tích hình vuông A 99 B 99 C 99 D 99 là S 100 = a 2 2 99
Vậy S = a 2 1 2 0 + 1 2 1 + 1 2 2 + ... + 1 2 99 ⏟ T
với T là tổng của CSN có u 1 = 1 ; q = 1 2 và n = 100
Do đó, tổng:
S = a 2 . 1 − 1 2 100 1 − 1 2 = 2 a 2 1 − 1 2 100 = a 2 2 100 − 1 2 99
Đúng 0
Bình luận (0)
Một căn phòng hình hộp chữ nhật có chiều dài 5 m, chiều rộng 4 m, chiều cao 3,5 m. Phòng có một cửa ra vào có diện tích 3,2 m2 và một cửa sổ có diện tích 1,5 m2. Người ta sơn toàn bộ tường trong và trần nhà của căn phòng đó. Tính diện tích cần sơn.
Diện tích trần nhà là:
\(5\text{x}4=20\left(m^2\right)\)
Chu vi trần nhà là:
\(\left(5+4\right)\text{x}2=18\left(m\right)\)
Diện tích xung quanh căn phòng là:
\(18\text{x}3,5=63\left(m^2\right)\)
Diện tích xung quanh cần sơn là:
\(63-3,2=59,8\left(m^2\right)\)
Diện tích cần sơn là:
\(20+59,8=79,8\left(m^2\right)\)
Đáp số: \(79,8m^2\)
ND
SGK Toán 3 tập 2- Bộ sách Cánh Diều - Trang 91
29 tháng 3 2023 lúc 16:00
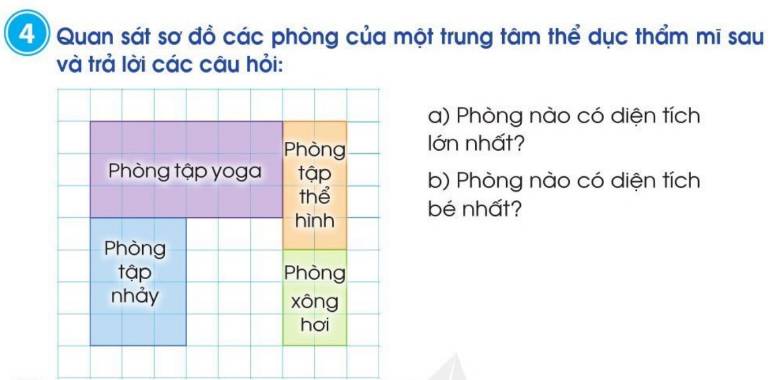
Quan sát sơ đồ các phòng của một trung tâm thể dục thẩm mĩ sau và trả lời các câu hỏi:
.
a) Phòng nào có diện tích lớn nhất?
b) Phòng nào có diện tích bé nhất?
Phòng tập yoga là hình gồm 18 ô vuông.
Phòng tập thể hình là hình gồm 10 ô vuông.
Phòng tập nhảy là hình gồm 12 ô vuông.
Phòng xông hơi là hình gồm 4 ô vuông.
a) Phòng tập yoga có diện tích lớn nhất.
b) Phòng xông hơi có diện tích bé nhất.
Đúng 0
Bình luận (0)
1. Một đường tròn và 1 hình vuông có cùng chu vi là 20 cm. Gọi S1 là diện tích hình tròn và S2 là diện tích hình vuông. Khẳng định nào sau đây đúng: A. S1 S2 B. S1 S2 C. S1 S2 D. S1 S2 + 22. Nếu a x b ( a - b ) : 2 thì giá trị của 2018 x 6 là: A. 2012 B. 1006 C. 1009 D. 20153. Một cửa hàng niêm yết giá bán một chiếc tivi là 13 400 000 đồng. Nếu bán chiếc tivi này...
Đọc tiếp
1. Một đường tròn và 1 hình vuông có cùng chu vi là 20 cm. Gọi S1 là diện tích hình tròn và S2 là diện tích hình vuông. Khẳng định nào sau đây đúng: A. S1 < S2 B. S1 > S2 C. S1 = S2 D. S1 = S2 + 2
2. Nếu a x b = ( a - b ) : 2 thì giá trị của 2018 x 6 là: A. 2012 B. 1006 C. 1009 D. 2015
3. Một cửa hàng niêm yết giá bán một chiếc tivi là 13 400 000 đồng. Nếu bán chiếc tivi này băng 50% giá niêm yết thì lãi 25% so với tiền vốn. Vậy tiền vón của chiếc tivi đó là: A. 6 700 00 đ B. 5 025 000 đ C. 4 020 000 đ D. 5 360 000 đ
