cho tam giác ABC AB nhỏ hơn AC đường cao AH gọi MNP lần lượt là trung điểm của các cạch BC CA AB
CT
Những câu hỏi liên quan
Bài 2: (3 điểm) Cho tam giác ABC. Biết AC = 16cm, AB=BC=10cm. Lấy D đối xứng của C qua B. Tính độ dài AD. (HS tự vẽ hình)
Bài 3: (4 điểm) Cho tam giác ABC (AB < AC), đường cao AH. Gọi M, N, P lần lượt là trung điểm AB, AC, BC. Chứng minh tứ giác MNPH là hình thang cân
mn giúp mik vs mik gần nộp cho thầy r (cảm mơn các bn nào giúp mik)
Bài 2:
D là điểm đối xứng của C qua B nên \(BC=BD\)
Lại có \(AB=BC=10\left(cm\right)\)
\(\Rightarrow AB=\dfrac{CD}{2}\)
Do đó tam giác ADC vuông tại A
Theo định lí Pitago ta có:
\(AD^2=DC^2-AC^2=20^2-16^2=144\)
\(\Rightarrow AD=12\left(cm\right)\)
Đúng 1
Bình luận (0)
Bài 3:
Vì M,N là trung điểm AB,AC nên MN là đtb tg ABC
Do đó MN//BC hay MN//PH
Do đó MNPH là hình thang
Xét tg AHC vuông tại H có HN là trung tuyến ứng vs ch AC nên \(HN=\dfrac{1}{2}AC\)
Mà P,M là trung điểm BC,AB nên PM là đtb tg ABC
Do đó \(PM=\dfrac{1}{2}AC\)
Từ đó ta được PM=HN
Vậy MNPH là hình thang cân
Đúng 1
Bình luận (0)
Cho tam giác ABC(AB<AC), đường cao AH. GỌi M, N, P lần lượt là là trung điểm các cạnh BC, CA,AB. Chứng minh rầng, NP là đường trung trực của AH
b,tứ giác MNPQ là hình thang cân
cho tam giác ABC( AB nhỏ hơn AC)đường cao AH.gọi M,N,P lần lượt là trung điểm của BC,AC,AB. a)cm: NP là đường trung trực của AH. b)cm: PH=MN
Xem chi tiết
a) gọi I là giao điểm của AH và PN
xét tam giác ABC có
AP=BF và AN=NC
Do đó PN là đường trung bình của tam giác ABC
==>PN//BC mà AH vuông góc BC ==>PN vuông góc AH (1)
ta có : PN//BC mà PI thuộc PN ==> PI//BC
Xét tam giác AHB có
PI//BC và AP=BP
==>AI=IH (2)
TỪ (1)(2) ==)PN là đg trung trực của AH
Cho tam giác ABC có góc A= 90o, AB<AC, đường cao AH. Gọi M,N,P lần lượt là trung điểm của các cạnh BC, CA, AB. Biết AH= 4cm, AM= 5cm. Tính các cạnh của tam giác ABC
ta có: AM=5 => BC=5.2=10(cm)
mặt khác HM2=AM2-AH2=25-16=9
=> HM=3
=> HB=5-3=2(cm)=> AB2=AH2+HB2=16+4=20
=> AB= căn 20
=> AC................
Đúng 0
Bình luận (0)
Cho tam giác ABC (AB < AC < BC), đường cao AH. Gọi D, E, F lần lượt là trung điểm của các cạnh AB, BC và AC. Gọi I là giao điểm của DF và AE.
b) Chứng I là trung điểm của DF.
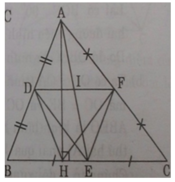
b) Ta có DF // BC (cmt) hay DI // BE; D là trung điểm của AD ⇒ I là trung điểm của AE và DI = BE/2
Trong ΔAEC có IF là đường trung bình nên IF = EC/2 mà EC = EB (gt) ⇒ IF = ID hay I là trung điểm của DF.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Gọi I là tâm đường tròn nội tiếp tam giáo ABC, các tiếp điểm trên BC, CA, AB lần lượt là D,E,F. Gọi M là trung điểm của AC, đường thẳng MI cắt cạnh AB tại N, đường thẳng DF cắt đường cao AH của tam giác ABC tại P. Chứng minh tam giác ANP là tam giác cân.
Cho tam giác ABC (AB>AC) đường cao AH. Gọi M,N,P lần lượt là trung điểm của BC,CA,AB. CMR:
a. NP là đường trung trực của AH
b. MHNP là hình thang cân
mng giải cho mình với nhé ( kèm hình )
a: Ta có: ΔAHB vuông tại H
mà HP là đường trung tuyến
nên HP=AP
hay P nằm trên đường trung trực của AH(1)
Ta có: ΔAHC vuông tại H
mà HN là đường trung tuyến
nên HN=AN
hay N nằm trên đường trung trực của AH(2)
Từ (1) và (2) suy ra PN là đường trung trực của AH
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Gọi I là tâm đường tròn nội tiếp tam giác ABC, các tiếp điểm BC, CA, AB lần lượt là D, E, F. Gọi M là trung điểm AC, đường thẳng MI cắt cạnh AB tại N, đường thẳng DF cắt đường cao AH của △ABC tại P.
Chứng minh rằng tam giác APN là tam giác cân
(Đề hay quá!)
Gọi \(X\) là trung điểm \(BC\). CM được \(DF,AI,MN\) đồng quy tại điểm ta gọi là \(K\).
Theo tính chất đường trung bình ta có \(MN\) song song \(AB\).
Do tam giác \(ABC\) vuông tại \(A\) cũng suy ra \(AB\) song song với \(IE\).
Áp dụng định lí Thales liên tục ta có:
\(\frac{AN}{IE}=\frac{MN}{MI}=\frac{KA}{KI}=\frac{AP}{ID}\).
Do \(ID=IE\) nên \(AN=AP\). Kết thúc chứng minh.
Đúng 0
Bình luận (0)
ê,chứng minh AI,DF,MX đồng quy kiểu gị ?
Đúng 0
Bình luận (0)
Cho tam giác ABC (AB<AC) đường cao AH. Gọi M, N, P lần lượt là trung điểm của cạnh BC, CA, AB. Chứng minh rằng:
a) NP là đường trung trực của AH
b) Tứ giác MNPH là hình thang cân



