Tìm các số nguyên n để n+4 chia hết cho n+1
Mọi người giúp hộ em với ạ !
Tìm các số nguyên n để n+4 chia hết cho n+1.
Giải hộ mình với !
Ta có : n + 4 \(⋮\)n + 1
\(\Leftrightarrow\)( n + 1 ) + 3 \(⋮\)n + 1
\(\Leftrightarrow\)n + 1 \(\in\)Ư( 3 ) = { \(\pm\)1 ; \(\pm\)3 }
Ta lập bảng :
| n + 1 | 1 | - 1 | - 3 | 3 |
| n | 0 | - 2 | - 4 | 2 |
Vậy : .............
Mik chưa hiểu cho lắm bạn oi ?????????????????????????????????????
Dễ hiểu mà bạn.
Đầu tiên, bạn tách n+4 thành n+1+3 để n+1 chia hết cho n+1
=> 3 phải chia hết cho n+1
Sau đó bạn tìm n như thường
Tìm số nguyên n để :2n-4 chia hết cho n+2
Các bạn ơi giúp mình vs!Thankiu ạ:3
Có 2n-4 chia hết cho n+2
=>2(n+2)8 chia hết cho n+2
=> 8 chia hết cho n+2
=>n+2 thuộc Ư(8)={1;2;4;8;-1;-2;-4;-8}
Phần cuối bạn tự làm nha
Để \(2n-4⋮n+2\)
\(\Leftrightarrow2n+4-8⋮n+2\)
\(\Leftrightarrow2\left(n+2\right)-8⋮n+2\)
Vì \(2\left(n+2\right)⋮n+2\)( vì \(n\in Z\))
\(\Rightarrow8⋮n+2\)
\(\Leftrightarrow n+2\inƯ\left(8\right)\)( vì \(n\in Z\))
\(\Leftrightarrow n+2\in\left\{1;-1;2;-2;4;-4;8;-8\right\}\)
\(\Leftrightarrow n\in\left\{-1;-3;0;-4;2;-6;6;-10\right\}\)
=> 2.(n+2) chia hết cho n+2
=> 2n+4 chia hết cho n+2
Do đó, 2n-4 + (2n+4) chia hết cho n+2
=> 2n-4 + 2n-4 chia hết cho n+2
=> 0 chia hết cho n+2
=> n+2 thuộc Ư (0) {0}
Ta có bảng sau:
| n+2 | 0 |
| n | -2 |
Vậy n = -2
Mn giúp mik vs ạ ! Đang gấp ak.
Bài 6. Tìm số nguyên n để
a) n + 5 chia hết cho n -1 ;
b) 2n - 4 chia hết cho n + 2
c) 6n + 4 chia hết cho 2n + 1
d) 3 - 2n chia hết cho n+1
a, Ta có : \(\text{n + 5 = (n - 1)+6}\)
Vì \(\text{(n-1) ⋮ n-1}\)
Nên để \(\text{n+5 ⋮ n-1}\)⋮ `n-1`
Thì \(\text{6 ⋮ n-1}\)
\(\Rightarrow\) \(\text{n - 1 ∈ Ư(6)}\)
\(\Rightarrow\) \(\text{n - 1 ∈}\) \(\left\{\text{±1;±2;±3;±6}\right\}\)
\(\Rightarrow\) \(\text{n ∈}\) \(\left\{\text{0;-1;-2;-5;2;3;4;7}\right\}\) \(\text{( TM )}\)
\(\text{________________________________________________________}\)
b, Ta có : \(\text{2n-4 = (2n+4)- 8 = 2(n+2) - 8}\)
Vì \(\text{2(n+2) ⋮ n+2}\)
Nên để \(\text{2n-4 ⋮ n+2}\)
Thì \(\text{8 ⋮ n+2}\)
\(\Rightarrow\) \(\text{n + 2 ∈ Ư(8)}\)
\(\Rightarrow\) \(\text{n + 2 ∈}\) \(\left\{\text{±1;±2;±4;±8}\right\}\)
\(\Rightarrow\) \(\text{n ∈}\) \(\left\{\text{-3;-4;-6;-10;-1;0;2;6}\right\}\) ( TM )
\(\text{_________________________________________________________________ }\)
c, Ta có :\(\text{ 6n + 4 = (6n + 3) +1 = 3(2n+1) + 1}\)
Vì \(\text{3(2n+1) ⋮ 2n+1}\)
Nên để\(\text{ 6n+4 ⋮ 2n+1}\)
Thì \(\text{1 ⋮ 2n+1}\)
\(\Rightarrow\) \(\text{2n + 1 ∈ Ư(1)}\)
\(\Rightarrow\) \(\text{2n + 1 ∈}\) \(\left\{\text{±1}\right\}\)
\(\Rightarrow\) \(\text{2n ∈}\) \(\left\{\text{-2;0}\right\}\)
\(\Rightarrow\) \(\text{n ∈}\) \(\left\{\text{-1;0}\right\}\) ( TM )
\(\text{_______________________________________}\)
Ta có : \(\text{3 - 2n = -( 2n - 3 ) = -( 2n + 2 ) + 5 = -2( n+1)+5}\)
Vì \(\text{-2(n+1) ⋮ n+1}\)
Nên để \(\text{3-2n ⋮ n+1}\)
Thì\(\text{ 5 ⋮ n + 1}\)
\(\Rightarrow\) \(\text{n + 1 ∈}\) \(\left\{\text{±1;±5}\right\}\)
\(\Rightarrow\) \(\text{n ∈}\) \(\text{-2;-6;0;4}\) ( TM )
a) Tìm các số nguyên n sao cho 3n chia hết cho n-1
b) Tìm các sô nguyên n sao cho 2n+5 chia hết cho n+2
Giúp em với chiều em nộp rồi !!!!!! Cảm ơn
giải các bài toán sau :
a) tìm số nguyên n sao cho n+2 chia hết cho n-3
b) tìm các giá trị nguyên của x để x-3 là ước của 13
c) tìm các giá trị nguyên của x để x-2 là ước của 111
d) tìm các số nguyên n sao cho 5 chia hết cho n+ 15
e) tìm các số nguyên n sao cho 3 chia hết cho n+ 24
f) tìm các số nguyên sao cho : ( 4x + 3 ) chia hết ( x-2 )
giúp mình với !!!
a)n=5
b)X=16;-10;2;4
c)x=113;39;5;3;1;-1;-35;-109
Answer:
a) \(\left(n+2\right)⋮\left(n-3\right)\)
\(\Rightarrow\left(n-3+5\right)⋮\left(n-3\right)\)
\(\Rightarrow5⋮\left(n-3\right)\)
\(\Rightarrow n-3\) là ước của \(5\), ta có:
Trường hợp 1: \(n-3=-1\Rightarrow n=2\)
Trường hợp 2: \(n-3=1\Rightarrow n=4\)
Trường hợp 3: \(n-3=5\Rightarrow n=8\)
Trường hợp 4: \(n-3=-5\Rightarrow n=-2\)
b) Ta có: \(x-3\inƯ\left(13\right)=\left\{\pm1;\pm13\right\}\)
\(\Rightarrow x\in\left\{4;16;2;-10\right\}\)
Vậy để \(x-3\inƯ\left(13\right)\Rightarrow x\in\left\{4;16;2;-10\right\}\)
c) Ta có: \(x-2\inƯ\left(111\right)\)
\(\Rightarrow x-2\in\left\{\pm111;\pm37;\pm3;\pm1\right\}\)
\(\Rightarrow x\in\left\{-99;-35;1;1;3;5;39;113\right\}\)
d) \(5⋮n+15\Rightarrow n+15\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)
Trường hợp 1: \(n+15=-1\Rightarrow n=-16\)
Trường hợp 2: \(n+15=1\Rightarrow n=-14\)
Trường hợp 3: \(n+15=5\Rightarrow n=-10\)
Trường hợp 4: \(n+15=-5\Rightarrow n=-20\)
Vậy \(n\in\left\{-14;-16;-10;-20\right\}\)
e) \(3⋮n+24\)
\(\Rightarrow n+24\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow n\in\left\{-23;-25;-21;-27\right\}\)
f) Ta có: \(x-2⋮x-2\)
\(\Rightarrow4\left(x-2\right)⋮x-2\)
\(\Rightarrow4x-8⋮x-2\)
\(\Rightarrow\left(4x+3\right)-\left(4x-8\right)⋮x-2\)
\(\Rightarrow11⋮x-2\)
\(\Rightarrow x-2\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
\(\Rightarrow x\in\left\{3;13;1;-9\right\}\)
4x-3⋮x-2
--> 4(x-2)+5⋮x-2
--> 5⋮x-2 (vì 4(x-2)⋮ x-2)
-->x-2⋴Ư(5) =⩲1;⩲5
ta có bảng
| x-2 | 1 | -1 | 5 | -5 |
| x | 3 | 1 | 7 | -3 |
vậy x=1;3;7;-3 thì 4x-3⫶x-2
Mọi người giúp em một bài toán chia hết lớp 9 ạ!
Chứng minh rằng với mọi số nguyên m, tồn tại số nguyên n sao cho n³-11n²-87n+m chia hết cho 191
tìm số nguyên n để n+8 chia hết cho n+3,mọi người nhanh hộ mk nhé
ta có :
n+8:n+3
\(\Rightarrow\)(n+3)+5:n+3
\(\Rightarrow\)5:n+3
\(\Rightarrow\)n+3\(\in\){1;5} ( vì là số tự nhiên )
+)n+3=1\(\Rightarrow\)n=-2(loại)
=)n+3=5\(\Rightarrow\)n=2(chọn )
vậy n=2
n=2 gjjgfg
Tìm số nguyên n để:
a,n+5 chia hết cho n-1
n+5 chia hết cho n+2
b,2n-4 chia hết cho n+2
c,6n+4 chia hết cho 2n+1
d,3-2n chia hết cho n+1
Bạn nào giải được thì giúp em với nhé,em cảm ơn trước vậy!
a) n+5 chia hết cho n-1
Ta có: n+5 = (n-1)+6
=> n-1 và 6 cùng chia hết cho n-1 hay n-1\(\in\)Ư(6)={-1;1;-2;2;-3;3;-6;6}
=> n\(\in\){0;2;-1;3;-2;4;-5;7}
b) n+5 chia hết cho n+2
Ta có: n+5 = (n+2)+3
=> n+2 và 3 cùng chia hết cho n+2 hay n+2\(\in\)Ư(3)={-1;1;-3;3;}
=> n\(\in\){-3;-1;-5;1;}
c) 2n-4 chia hết cho n+2
Ta có: 2n-4 = 2(n+2)-8
=> 2(n+2) và 8 cùng chia hết cho n+2 hay n+2\(\in\)Ư(8)={-1;1;-2;2;-4;4;-8;8}
=> n\(\in\){-3;-1;-4;0;-6;2;-10;6}
d) 6n+4 chia hết cho 2n+1
Ta có: 6n+4 = 3(2n+1)+1
=> 3(2n+1) và 1 cùng chia hết cho 2n+1 hay 2n+1\(\in\)Ư(1)={-1;1;}
=> n\(\in\){-1;0}
e) 3-2n chia hết cho n+1
Ta có: 3-2n= -2(1+n)+5
=> -2(1+n) và 5 cùng chia hết cho n+1 hay n+1\(\in\)Ư(5)={-1;1;-5;5;}
=> n\(\in\){-2;0;-6;4;}
Mọi người giúp em 4 bài này với mọi người giải bằng tiếng việt hay là tiếng anh cũng dc ạ (tiếng anh thì tốt ạ)
bài 1:Gọi n là số tự nhiên sao cho n + 1 và 2n + 1 đều là số chính phương . Chứng minh rằng n chia hết cho 24.
bài2:Tìm tất cả các số tự nhiên n sao cho 2n + 1,3n + 1 đều là bình phương hoàn hảo và 6n + 5 là số nguyên tố.
bài3:tìm các số nguyên a, b, c sao cho a^4 + b^4 = 7c^4 +5.
bài4:Tìm tất cả các số nguyên dương x, y và các số nguyên tố p sao cho x^2 −3xy + p^2y^2 = 12p.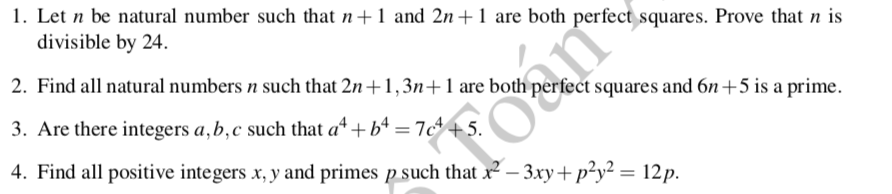
- Chắc là gọi thầy Nguyễn Việt Lâm thôi :)
1.
\(2n+1\) luôn lẻ \(\Rightarrow2n+1=\left(2a+1\right)^2=4a^2+4a+1\Rightarrow n=2a\left(a+1\right)\)
\(\Rightarrow n\) chẵn \(\Rightarrow n+1\) lẻ \(\Rightarrow\) là số chính phương lẻ
\(\Rightarrow n+1=\left(2b+1\right)^2=4b^2+4b+1\)
\(\Rightarrow n=4b\left(b+1\right)\)
Mà \(b\left(b+1\right)\) là tích 2 số tự nhiên liên tiếp \(\Rightarrow\) luôn chẵn
\(\Rightarrow4b\left(b+1\right)⋮8\Rightarrow n⋮8\)
Mặt khác số chính phương chia 3 chỉ có các số dư 0 và 1
Mà \(\left(n+1\right)+\left(2n+1\right)=3n+2\) chia 3 dư 2
\(\Rightarrow n+1\) và \(2n+1\) đều chia 3 dư 1
\(\Rightarrow n⋮3\)
\(\Rightarrow n⋮24\) do 3 và 8 nguyên tố cùng nhau
2.
Lý luận tương tự bài 1, ta được n chẵn
Mặt khác các số chính phương chia 5 chỉ có các số dư 0, 1, 4
Mà: \(\left(2n+1\right)+\left(3n+1\right)=5n+2\) chia 5 dư 2
\(\Rightarrow2n+1\) và \(3n+1\) đều chia 5 dư 1
\(\Rightarrow2n⋮5\Rightarrow n⋮5\) (do 2 và 5 nguyên tố cùng nhau)
\(\Rightarrow n=5k\Rightarrow6n+5=5\left(6k+1\right)\)
- TH1: \(k=0\Rightarrow n=0\Rightarrow6n+5\) là SNT (thỏa mãn)
- TH2: \(k>0\Rightarrow6k+1>0\Rightarrow6n+5\) có 2 ước dương lớn hơn 1 \(\Rightarrow\) không là SNT (loại)
Vậy \(n=0\) là giá trị duy nhất thỏa mãn yêu cầu