Cho tứ giác ABCD có góc A=90độ B=105độ C=75 độ. Biết rằng AD=2CD.Chứng minh rằng BD=CD
ND
Những câu hỏi liên quan
1. Cho hình thang ABCD có góc A góc D 90 độ , đáy nhỏ AB a , cạnh bên BC 2 a . Gọi M , N lần lượt là trung điểm AD , ABa / Tính số đo các góc ABC , BANb/ Chứng minh tam giác NAD đềuc/ Tính MN theo a 2. a/ Tính các góc A , góc B của hình thang ABCD ( AB // CD ) biết góc C 70 độ , góc D 40 độb/ Cho hình thang ABCD có AB // CD và góc A góc D . Chứng minh rằng ABCD là hình thang vuông cà AC^2 + BD^2 AB^2 + CD^2 + 2AD^23. Cho tứ giác ABCD :a/ Chứng minh rằng AB + CD AC + BDb/ Cho biết AB + B...
Đọc tiếp
1. Cho hình thang ABCD có góc A = góc D = 90 độ , đáy nhỏ AB = a , cạnh bên BC = 2 a . Gọi M , N lần lượt là trung điểm AD , AB
a / Tính số đo các góc ABC , BAN
b/ Chứng minh tam giác NAD đều
c/ Tính MN theo a
2. a/ Tính các góc A , góc B của hình thang ABCD ( AB // CD ) biết góc C = 70 độ , góc D = 40 độ
b/ Cho hình thang ABCD có AB // CD và góc A = góc D . Chứng minh rằng ABCD là hình thang vuông cà AC^2 + BD^2 = AB^2 + CD^2 + 2AD^2
3. Cho tứ giác ABCD :
a/ Chứng minh rằng AB + CD < AC + BD
b/ Cho biết AB + BD < hoặc = AC + CD
Chứng minh rằng AB < AC
4. Cho hình thang ABCD có AC vuông góc BD . CHứng minh rằng :
a/ AB^2 + CD^2 = AD^2 + BC^2
b/ ( AB + CD )^2 = AC^2 + BD^2
bạn hỏi thế này thì chả ai muốn làm -_- dài quá
Đúng 1
Bình luận (0)
Bạn gửi từng câu nhò thì các bạn khác dễ làm hơn!
Đúng 1
Bình luận (0)
dài quà làm sao mà có thòi gian mà trả lời .bạn hỏi ít thoi chứ
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
BÀI 1Cho hình thang vuông ABCD, góc Agóc D90độ.a) tìm điểm Ithuộc AD sao cho ICIBb)Với điểm I vừa tìm được, giả sử tam giác IBC vuông cân ở I, chứng minh rằng AB+CDADc) Với điểm I vừa tìm được, giả sử DC1/2 IC,hãy tính góc Bvà C của hình thang ABCDBÀI 2Cho tứ giác ABCD, có phân giác góc A cắt CD tại I, biết ICBC và DCAD+BC. Chứng minh: a) ABCD là hình thangb) BI là phân giác góc ABCBÀI 3Cho hình thang ABCD có AB//CD có góc B-góc C24 độ, góc A3/2góc B. Tính các góc còn lạiBÀI 4 :Cho tam giác vuôn...
Đọc tiếp
BÀI 1
Cho hình thang vuông ABCD, góc A=góc D=90độ.
a) tìm điểm Ithuộc AD sao cho IC=IB
b)Với điểm I vừa tìm được, giả sử tam giác IBC vuông cân ở I, chứng minh rằng AB+CD=AD
c) Với điểm I vừa tìm được, giả sử DC=1/2 IC,hãy tính góc Bvà C của hình thang ABCD
BÀI 2
Cho tứ giác ABCD, có phân giác góc A cắt CD tại I, biết IC=BC và DC=AD+BC. Chứng minh:
a) ABCD là hình thang
b) BI là phân giác góc ABC
BÀI 3
Cho hình thang ABCD có AB//CD có góc B-góc C=24 độ, góc A=3/2góc B. Tính các góc còn lại
BÀI 4 :
Cho tam giác vuông can A, trên nửa mặt phẳng bờ là BC không chứa A vẽ BD vuông góc BC và BD=BC. Chứng minh :
a) Tứ giác ABCD là hình gì?
b) Tính CD, biết AB=5
MONG MỌI NGƯỜI GIÚP ĐỠ Ạ! MÌNH CẢM ƠN :))
Cho tứ giác ABCD có BD là phân giác của góc ABC , AD = CD , AB < BC . Chứng minh rằng : góc C + góc A = 180 độ.
mình cảm ơn.
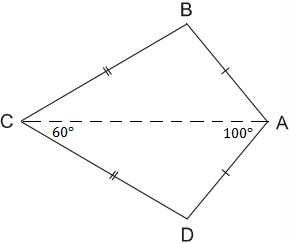
Ta gọi tứ giác ABCD có AB=AD,CB=CD là hình “cái diều”.
a)CMinh rằng AC là đường trung trực của BD.
b)Tính góc B,góc D biết rằng góc A=100 độ,góc C=60 độ.
c)Giả sử cho góc ABC=117 độ,góc BAD bằng 2 lần góc BCD.Tính các góc của tứ giác ABCD.
a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
nên ∆ ABC = ∆ADC (c.c.c)
Suy ra: ⇒ˆB=ˆD
Ta có ˆB+ˆD=3600–(100+60)=200
Do đó ˆB=ˆD=1000
Đúng 1
Bình luận (0)
mban trl giúp mình câu C luôn nha ạ😭
Đúng 0
Bình luận (0)
Mình làm hơi tắt
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
Mà \(\widehat{A}=2\times\widehat{C}\left(gt\right)\)
\(\widehat{B}=\widehat{D}=117^o\)theo câu b)
\(\Rightarrow2\times\widehat{C}+117^o+\widehat{C}+117^o=360^o\)
\(\Rightarrow3\times\widehat{C}=360^o-117^o-117^o=126^o\)
\(\Rightarrow\widehat{C}=\frac{126^o}{3}=42^o\)
\(\Rightarrow\widehat{A}=2\times\widehat{C}=2\times42^o=84^o\)
Vậy \(\widehat{A}=84^o;\widehat{B}=117^o;\widehat{C}=42^o;\widehat{D}=117^o\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 1: Hình thang cân ABCD (AB song song CD) có AB=11cm, BC=CD=25cm. Tính độ dài BD
Bài 2:Tứ giác ABCD có góc B = 105 độ, góc D = 75 độ, AB = BC = CD. Chứng minh rằng:
a) AC là tia phân giác góc A
b) ABCD là hình thang cân?
cho tứ giác ABCD có góc ACD + góc BCD= 90độ. Gọi E,F.G.H lần lượt là trung điểm của các đoạn thẳng AB, AC, CD, BD.
Chứng minh rằng tứ giác EFGH là hình chữ nhật
Cho hình thoi ABCD(gócA<90độ) trên AD lấy M , trên CD lấy N sao cho AM=CN a) chứng minh tam giác BMN cân. b) chứng minh BD vuông góc với MN. c) biết góc A =60 độ ,M và N lần lượt là trung điểm của AD và CD,tính số đo góc BMN
a: Xét ΔBAM và ΔBCN có
BA=BC
góc BAM=góc BCN
AM=CN
Do đó: ΔBAM=ΔBCN
=>BM=BN
=>ΔBMN cân tại B
b: DM+MA=DA
DN+NC=DC
mà DA=DC và MA=NC
nên DM=DN
BM=BN
DM=DN
Do đó: BD là trung trực của MN
=>BD vuông góc MN
c: Xét ΔABD có AB=AD và góc A=60 độ
nên ΔABD đều
ΔABD đều có BM là trung tuyến
nên BM là phân giác của góc ABD(1)
Xét ΔCBD có CB=CD và góc C=60 độ
nên ΔCBD đều
ΔCBD đều có BN là trung tuyến
nên BN là phân giác của góc DBC(2)
Từ (1), (2) suy ra góc MBN=1/2(góc ABD+góc CBD)
=1/2*góc ABC
=60 độ
Xét ΔBMN có BM=BN và góc MBN=60 độ
nên ΔBMN đều
=>góc BMN=60 độ
Đúng 0
Bình luận (0)
1. Cho hình thang ABCD(AB//CD). M là trung điểm của BC. Cho biết DM là tia phân giác của góc D. Chứng minh rằng tia AM là tia phân giác của góc A.
2.Tứ giác ABCD có AD=BC và AC=BD. Chứng minh rằng ABCD là hình thang cân.
Xét ▲ADC và ▲BCD có:
AD = BC ( gt )
AC = BD ( gt )
DC chung
=> ▲ADC = ▲BCD ( c.c.c )
=> góc D = góc C ( c.t.ứ )
cmtt ta đc góc A = Góc B
Mà Góc D + góc A + Góc C + Góc B=360o
=> 2GócA+2GócD=360o
-> gócA+gócD=180o ( 2 góc trong cùng phía )=>AB//DC -> ABCD là hình thang
Vì góc D = góc C (cmt) nên ABCD là hình thang cân
Câu 1: tam giác ABC có góc B lớn hơn 90 độ và nhỏ hơn 130 độ. Kẻ AD vương gócvới BC. CM BD <AD<CD
Câu 2:tam giác ABC có góc A bằng 90độ. chứng minh rằng góc C bằng 30 độ khi và chỉ khi AB=1/2 BC

