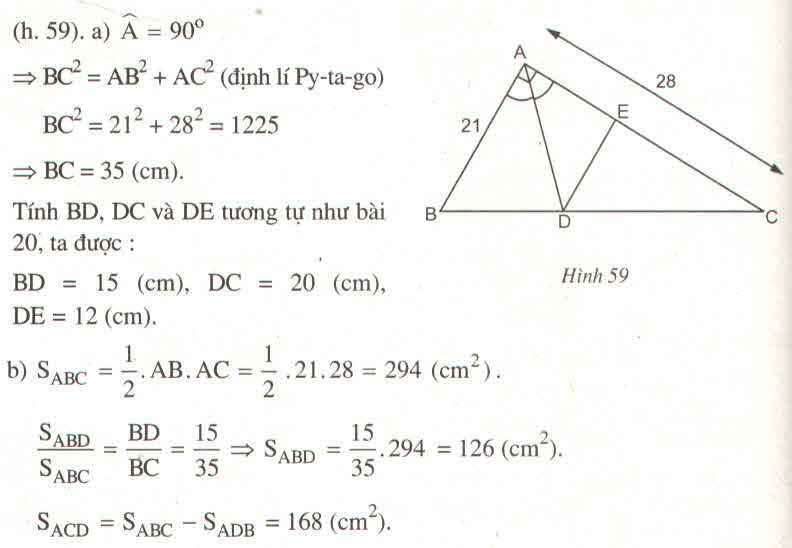
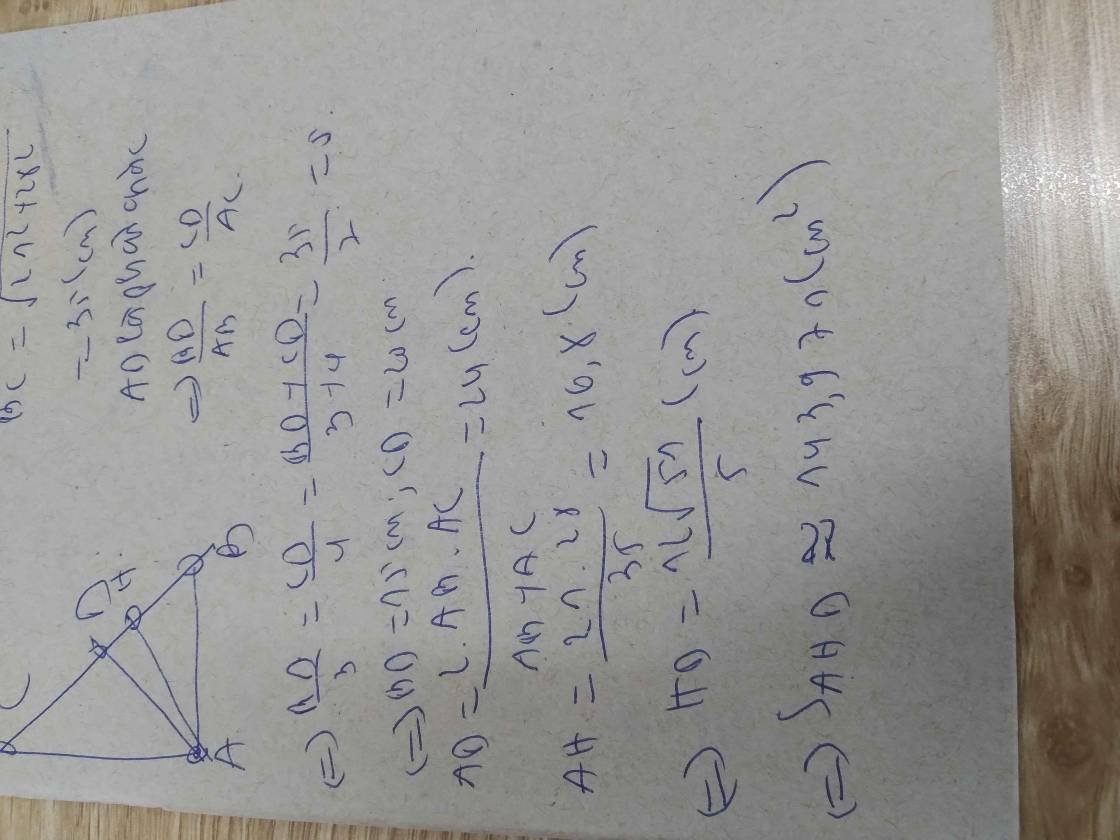Cho tam giác ABC vuông tại A,AB=21cm,AC=28cm,đường phân giác AD.Tính khoảng cách từ D đến AC
DD
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, AB = 21cm, AC = 28cm; đường phân giác góc A cắt BC tại D, đường thắng qua D song song với AB cắt AC tại E. Tính diện tích tam giác ABD và diện tich tam giác ACD.
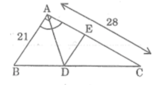
Ta có: S A B C = 1/2.AB.AC = 1/2.21.28 = 294 ( c m 2 )
Vì △ ABC và △ ADB có chung đường cao kẻ từ đỉnh A nên:
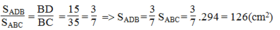
Vậy S A D C = S A B C - S A B D = 294 – 126 = 168( c m 2 )
Đúng 0
Bình luận (0)
.cho tam giác vuông ABC ( góc A= 90 độ) AB=28cm, AC=21cm đường phân giác góc A cắt BC tại D đường thẳng qua D và song song với AC, cắt AB tại E.
a) tính BD, BC và DE
Cho tam giác ABC vuông tại A, AB = 21cm, AC = 28cm; đường phân giác góc A cắt BC tại D, đường thắng qua D song song với AB cắt AC tại E. Tính độ dài các đoạn thẳng BD,DC và DE.
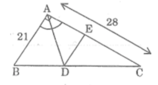
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2 = 21 2 + 28 2 = 1225
Suy ra: BC = 35 (cm)
Vì AD là đường phân giác của ∠ (BAC) nên:
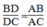 (t/chất đường phân giác)
(t/chất đường phân giác)
Suy ra: 
Hay 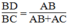
Suy ra: 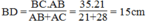
Vậy DC = BC – BD = 35 – 15 = 20cm
Trong ΔABC ta có: DE // AB
Suy ra: 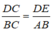 (Hệ quả định lí Ta-lét)
(Hệ quả định lí Ta-lét)
Suy ra: 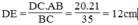
Đúng 0
Bình luận (0)
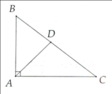
Cho ΔABC vuông tại A, đường cao AH và đường phân giác AD (H và D thuộc BC). Biết AB = 21cm, AC = 28cm.
a) Tính diện tích tam giác ABC và chứng minh AH . BC = AB . AC
\(S_{ABC}=\dfrac{AB.AC}{2}=\dfrac{21.28}{2}=294\left(cm^2\right)\)
Ta có:\(S_{ABC}=\dfrac{AB.AC}{2}\) mà ta lại có: \(S_{ABC}=\dfrac{AH.BC}{2}\)
\(\Rightarrow\dfrac{AB.AC}{2}=\dfrac{AH.BC}{2}\Rightarrow AB.AC=AH.BC\left(đpcm\right)\)
Đúng 3
Bình luận (4)
Cho tam giác ABC vuông tại A(góc A=90°),AB=21cm,AC=28cm. Vẽ đường cao AH(H thuộc BC). Tia phân giác của góc A cắt BC tại D. Tính BC,BD,CD và diện tích tam giác AHD
Xét ΔABC vuông tại A, áp dụng định lí py-ta-go ta có:
\(BC^2=AB^2+AC^2\)
\(=21^2+28^2\)
\(=1225\)
->\(BC=\sqrt{1225}=35\left(cm\right)\)
Xét ΔABC có AD là tia phân giác ta có:
\(\dfrac{AB}{BD}=\dfrac{AC}{CD}=\dfrac{AB+AC}{BC}hay\dfrac{21}{BD}=\dfrac{28}{CD}=\dfrac{21+28}{35}=\dfrac{7}{5}\)
⇒\(BD=\dfrac{21.5}{7}=15\left(cm\right)\)
⇒\(CD=\dfrac{28.5}{7}=20\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có AB=21cm, AC=28cm, đường phân giác AD.
Tính độ dài cạnh AD
Cho ΔABC vuông tại A, đường cao AH và đường phân giác AD (H và D thuộc BC). Biết AB = 21cm, AC = 28cm.
a) Tính diện tích tam giác ABC và chứng minh AH . BC = AB . AC
b) Tính độ dài BC, DB và DC.
c) Đường phân giác BK của ABC cắt AD tại I (K thuộc AC), tính tỉ số BI/IK . Gọi G là trọng tâm ΔABC, chứng minh IG //AC.
a: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot21\cdot28=294\left(cm^2\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\)
mà \(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\)
nên \(AH\cdot BC=AB\cdot AC\)
b: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=21^2+28^2=1225\)
=>\(BC=\sqrt{1225}=35\left(cm\right)\)
Xét ΔABC có AD là phân giác
nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)
=>\(\dfrac{DB}{15}=\dfrac{DC}{20}\)
=>\(\dfrac{DB}{3}=\dfrac{DC}{4}\)
mà DB+DC=BC=35cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{35}{7}=5\)
=>\(DB=5\cdot3=15\left(cm\right);DC=4\cdot5=20\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, có AB = 21cm, AC = 28cm. Kẻ phân giác trong AD của B A C ^ (với D ∈ B C ). Tính BD, CD
Cho tam giác ABC vuông tại A, biết AB = 21cm, AC= 28cm, phân giác AD( D thuộc BC). Đường thẳng qua D song song với BA cắt CA tại E. Tính độ dài DB, DC, ED.