làm ơn hãy giúp mình mình cần gấp trước 3 giờ mình cảm ơn trước

làm ơn hãy giúp mình , mình cần gấp trước 8 giờ làm ơn đó🙏🙏🙏

Bài 1:
Vì AD là p/g góc A nên \(\widehat{A_1}=\widehat{A_2}=\dfrac{1}{2}\widehat{BAC}=30^0\)
Mà \(\widehat{A_2}+\widehat{C}+\widehat{D_1}=180^0\Rightarrow\widehat{D_1}=180^0-30^0-40^0=110^0\)
Mà AE//BC nên \(\widehat{EAD}=\widehat{D_1}=110^0\left(so.le.trong\right)\)
Vì DE//AC nên \(\widehat{A_2}=\widehat{D_2}=30^0\left(so.le.trong\right);\widehat{D_3}=\widehat{C}=40^0\left(đồng.vị\right)\)
Vì AE//BC nên \(\widehat{D_3}=\widehat{E}=40^0\)
Vậy các góc tg ADE là \(\widehat{A}=110^0;\widehat{D}=30^0;\widehat{E}=40^0\)
Bài 2:
a, Xét tg ABH và tg DBH có
\(\left\{{}\begin{matrix}\widehat{BAH}=\widehat{BDH}=90^0\\\widehat{ABH}=\widehat{DBH}\left(BH.là.p/g\right)\\BH.chung\end{matrix}\right.\\ \Rightarrow\Delta ABH=\Delta BDH\left(ch-gn\right)\\ \Rightarrow HA=HD\)
b, Xét tg AHE và tg DHC có
\(\left\{{}\begin{matrix}\widehat{AHE}=\widehat{DHC}\left(đối.đỉnh\right)\\\widehat{HAE}=\widehat{HDC}=90^0\\HA=HD\left(cmt\right)\end{matrix}\right.\\ \Rightarrow\Delta AHE=\Delta DHC\left(g.c.g\right)\\ \Rightarrow CD=AE\)
Mà \(AB=BD\left(\Delta ABH=\Delta DBH\right)\)
\(\Rightarrow AB+AE=BD+CD\\ \Rightarrow BE=BC\)
Vì \(AD=AB\) nên tg ABD cân tại B
Do đó \(\widehat{BAD}=\dfrac{180^0-\widehat{ABC}}{2}\left(1\right)\)
Vì \(BE=BC\) nên tg BEC cân tại B
Do đó \(\widehat{BEC}=\dfrac{180^0-\widehat{ABC}}{2}\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\Rightarrow\widehat{BAD}=\widehat{BEC}\) mà 2 góc này ở vị trí đồng vị nên AD//EC
giúp mình nha khẩn cấp mình cần gấp trước 3 giờ chiều mình cảm ơn trước

1)xét tứ giác EACD
EA//DC,ED//AC
=>EACD hình bình hành
E=C=40(hai góc đối)
ta có DAC=BAC/2=60/2=30(AD là tia pg)
mà ED//AC
=>ADE=DAC=30(so le)
xét tg EAD
E+ADE+EAD=180
EAD=180-ADE-E=180-30-40=110
2)
a)xét tgAHB và tgDHB
BAH=BDH=90,ABH=HBD(BH là tia pg),BH chung
=>tgAHB=tgDHB(cạnh huyền góc nhọn)
=>AH=HD,BA=BD
b)xét tg BDE và tgBAC
BA=BD,ABC chung,BAC=BDE=90
=>tgBDE=tgBAC(gcg)
=>BE=BC
xét tg BEC
BA/BE=BD/BC=>AD//EC(ta lét đảo)
à mik làm thiếu
c)xét BEK
ED cắt AC tại H
mà ED vuông BC,AC vuông BE
=>H là trực tâm
lại có BK cắt AC tại H
=>BK vuông EC
xét tg vuông BKC
BM=MC
=>MK=MB(đường trung tuyến ứng cạnh huyền)(1)
xét tg vuông BAC
BM=MC
=>AM=MB(đường trung tuyến ứng cạnh huyền)(2)
từ (1)(2)=>AM=MK
giúp mình mấy câu này nha khẩn cấp mình cần gấp trước 3 giờ mình cảm ơn trước

Cách ra nha bn ! Vs lại bài 3 hình ko cho độ thì lm sao mà lm đc đây?
Giúp mình bài này nha mình đang cần gấp trước 9 giờ mình cảm ơn trước

Có bjan nào biết làm câu này thì giúp mình nha mình đnag cần gấp trước 4 giờ (chỉ phải làm câu 4) mình cảm ơn nhiều 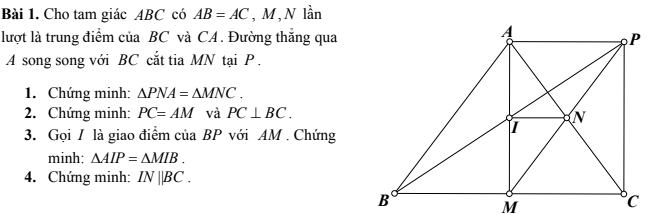
4: Ta có:ΔAIP=ΔMIB
nên IA=IM
hay I là trung điểm của AM
Xét ΔAMC có
I là trung điểm của AM
N là trung điểm của AC
Do đó: IN là đường trung bình của ΔAMC
Suy ra: IN//MC
hay IN//BC
Câu 4 Ta có xét tg PBM có PN=MN( tg PNA=tg MNC)
PI=BI( tg AIP= tgMIB)
=> IN là đường trung bình tg PBM
=>IN//BM <=> IN//BC
Có bạn nào biết làm câu này thì giúp mình nha mình đang cần gấp trước 12 giờ nếu được thì mình cảm ơn nhiều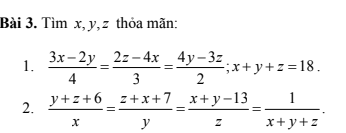
Có bạn nào biết làm 2 bài này thì giúp mình nha mình thực sự cần rất gấp trước 9 giờ mình cảm ơn nhiều

Có bạn nào biết làm câu này thì giúp mình nha mình đang cần gấp trước 4 giờ nếu bạn nào biết làm thì mình cảm ơn nhiều
1: Xét ΔABC có AB=AC
nên ΔABC cân tại A
Suy ra: \(\widehat{ABC}=\widehat{ACB}\)
Xét ΔABH và ΔACH có
AB=AC
AH chung
BH=CH
Do đó: ΔABH=ΔACH
Suy ra: \(\widehat{AHB}=\widehat{AHC}\)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
Do đó: AH\(\perp\)BC
Có bạn nào biết làm bài này thì giúp mình nha mình đang cần gấp trước 2 giờ( rất gấp rồi chỉ còn 1 tiếng) mình cảm ơn nhiều (KO dùng hình bình hành, đường cao, tam giác cân, đường trung tuyến hay các kiến thức lớp 8) .Làm ơn hãy trả lời nhanh

tam giác ABM và tam giác KBM có
BK=BA
BM là cạnh chung
BM là phân giác góc B = > góc ABM = góc KBM
=> tam giác ABM = tam giác KBM ( c.g.c)
b: Ta có: ΔABM=ΔKBM
nên \(\widehat{BAM}=\widehat{BKM}=90^0\)
Xét ΔAME vuông tại A và ΔKMC vuông tại K có
MA=MK
\(\widehat{AME}=\widehat{KMC}\)
Do đó: ΔAME=ΔKMC
Suy ra: ME=MC
\(a,\left\{{}\begin{matrix}\widehat{ABM}=\widehat{KBM}\left(t/c.phân.giác\right)\\AB=BK\left(gt\right)\\BM.chung\end{matrix}\right.\Rightarrow\Delta ABM=\Delta KBM\left(c.g.c\right)\\ b,\Delta ABM=\Delta KBM\Rightarrow\left\{{}\begin{matrix}\widehat{MAB}=\widehat{MKB}=90^0\\MA=MK\end{matrix}\right.\\ \left\{{}\begin{matrix}\widehat{MAE}=\widehat{MKC}\left(=90^0\right)\\MA=MK\\\widehat{AME}=\widehat{KMC}\left(đối.đỉnh\right)\end{matrix}\right.\Rightarrow\Delta AME=\Delta KMC\left(cgv-gn\right)\\ \Rightarrow ME=MC\)
\(c,\Delta BEC\) có CA là đường cao \(\left(CA\perp BE\right)\), EK là đường cao \(\left(EK\perp BC\right)\), EK cắt CA tại M nên M là trực tâm
Do đó BM là đường cao thứ 3
Mà \(M\in BI\) nên BI là đường cao thứ 3 của tam giác BEC
\(\Rightarrow BI\perp EC\)
\(d,\) Vì \(AB=BK\) nên tam giác ABK cân tại B
\(\Rightarrow\widehat{BAK}=\dfrac{180^0-\widehat{ABK}}{2}\left(1\right)\)
Ta có \(\left\{{}\begin{matrix}AB=BK\\AE=CK\end{matrix}\right.\Rightarrow AB+AE=BK+KC\Rightarrow BE=BC\)
Do đó tam giác BEC cân tại B
\(\Rightarrow\widehat{BEC}=\dfrac{180^0-\widehat{ABK}}{2}\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow\widehat{BAK}=\widehat{BEC}\)
Mà 2 góc này ở vị trí đồng vị nên \(AK//EC\)
\(\Rightarrow AK\perp BI\left(EC\perp BI\right)\) hay \(AK\perp MQ\left(Q\in BI;M\in BI\right)\)
Xét tam giác AQK có KH là đường cao \(\left(KH\perp AQ\right)\), QM là đường cao \(\left(AK\perp QM\right)\) và KH cắt QM tại M nên M là trực tâm
Do đó AM là đường cao thứ 3 hay \(AM\perp QK\)
Mà \(AM\perp PK\left(gt\right)\)
Nên PK trùng QK hay 3 điểm K,P,Q thẳng hàng