Tính giá trị biểu thức 8x^2y+5x^3 tại x,y thỏa mãn:(x+1)^30+(y+2)^50=0
H24
Những câu hỏi liên quan
Tính giá trị biểu thức 8x^2y+5x^3 tại x,y thỏa mãn:(x+1)^30+(y+2)^50=0
Lời giải:
Vì $(x+1)^{30}\geq 0$ với mọi $x\in\mathbb{R}$
$(y+2)^{50}\geq 0$ với mọi $y\in\mathbb{R}$
Do đó để tổng $(x+1)^{30}+(y+2)^{50}=0$ thì:
$(x+1)^{30}=(y+2)^{50}=0\Rightarrow x=-1; y=-2$
Khi đó:
$8x^2y+5x^3=8(-1)^2(-2)+5(-1)^3=-21$
1.Tính giá trị biểu thức: 6x^2+5x-2 tại x thõa mãn /x-2/=1
2.Tính giá trị biểu thức: 2x^8-3y^5+2 tại x,y thõa mãn (x+1)^20+(y+2)^26=0
3.Tính giá trị biểu thức: P=6x^3-4x^2y-14y^2+21xy+9 tại x,y thõa mãn 2x^2+7y=0
Mình đang cần gấp lắm ạ, mong mọi người giúp, mình cảm ơn nhiều ạ
cho x,y thỏa mãn đẳng thức 5x^2+5y^2+8xy-2x+2y+2=0
Tính giá trị biểu thức M=(x+y)^2015+(x-2)^2016+(y+1)^2017
kho....................wa..................troi.......................thi.....................ret.................lanh................wa..................tich............................ung.........................ho..............minh......................cho....................do....................lanh
Đúng 0
Bình luận (0)
Ta có: 5x2+5y2+8xy-2x+2y+2=0
=> 4x2+8xy+4y2+x2-2x+1+y2+2y+1=0
=> (2x+2y)2+(x-1)2+(y+1)2=0
=> {2x+2y=0 => x=-y
{x-1 = 0 => x=1
{y+1 =0 => y=-1
=> x=1, y=-1
Thay vào biểu thức M, ta có:
M=(1+-1)2015+(1-2)2016+(-1+1)2017=0+1+0=1 (đpcm)
Đúng 0
Bình luận (0)
cho x,y thỏa mãn đẳng thức 5x^2+5y^2+8xy-2x+2y+2=0
Tính giá trị biểu thức M=(x+y)^2015+(x-2)^2016+(y+1)^2017
giúp mình đi nha mình cần rất rất rất rất ...... gấp đấy !!!!=.='![]()
![]()
Đúng 0
Bình luận (2)
Xem thêm câu trả lời
Tính giá trị của biểu thức 2x^5 - 5x^3 + 4 tại x , y thỏa mãn ( x - 1 )^20 + ( y + 2 ) ^30 = 0
Nhanh lên nhé !!! Mik cần gấp lắm
cho các số x, y thỏa mãn\(\left(x+20\right)^4\)+\(\left(2y-1\right)^{2024}\)\(\le\)0
Tính giá trị biểu thức M=\(5x^2\)y-\(4xy^2\)
(x + 20)⁴ + (2y - 1)²⁰²⁴ ≤ 0
⇒ (x + 20)⁴ = 0 và (2y - 1)²⁰²⁴ = 0
*) (x + 20)⁴ = 0
x + 20 = 0
x = 0 - 20
x = -20
*) (2y - 1)²⁰²⁴ = 0
2y - 1 = 0
2y = 1
y = 1/2
M = 5.(-20)².1/2 - 4.(-2).(1/2)²
= 1000 + 2
= 1002
Đúng 1
Bình luận (0)
Cho các số thỏa mãn đẳng thức 5x^2 + 5y^2 +8xy - 2x + 2y + 2 = 0
Tính giá trị biểu thức M= (x+y)^2007 +(x-2)^2008 + (y+1)^2009
Cho các số x,y thỏa mãn đẳng thức 5x^2+5y^2+8xy-2x+2y+2=0.Tính giá trị của biểu thức M=(x+y)^2007+(x-2)^2008+(y+1)^2009
Cho x, y là các số thực dương thỏa mãn điều kiện
5
x
+
2
y
+
3
3
x
y
+
x
+
1
5
x
y
5
+...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn điều kiện 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 - x - 2 y + y ( x - 2 ) .Tính giá trị nhỏ nhất của biểu thức T = x + y
![]()
![]()
![]()
![]()
Đáp án B.
Từ giả thiết, suy ra
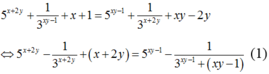
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 - ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f ( t ) luôn đồng biến trên ℝ .
Suy ra
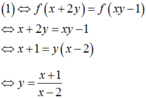
Do y > 0 nên x + 1 x - 2 > 0 ⇔ [ x > 2 x < - 1 . Mà x > 0 nên x > 2 .
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm
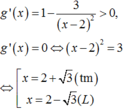
Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy min g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và x = 1 + 3 .
Đúng 0
Bình luận (0)



