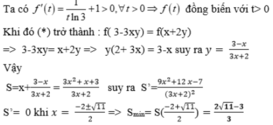Tìm các giá trị nguyên của x,y biết : \(3xy-5=x^2+2y\)
H24
Những câu hỏi liên quan
Tìm các giá trị nguyên của x và y biết : \(3xy-5=x^2+2y\)
Tìm nghiệm nguyên của phương trình x2+2y2+3xy-x-y+3=0
tinh giá trị biểu thức P=x-y/x+y biết x2-2y^2=xy(x+y khác 0 y khác 0)
Biết x+y=0,tính giá trị của đa thức sau :
C=2x+2y+3xy(x+y)+5(x^3y^2)+2
D= 3xy(x+y)+2x^3y+2x^2y^2+5
Phân tích đa thức thành nhân tủ
3x^2+y^2+2x-2y=1
x^3+y^3-3xy+x+y+2
Tìm giá trị nguyên của x,y:x^2+2xy+2y^2-4=0
giải các pt /x-2/ +/x-3/ + /2x-8/=9
1. cho x,y là các số dương thỏa mãn x + y < (h) = 1 .Tìm giá trị nhỏ nhất của biểu thức : A= \(\frac{1}{x^3+3xy^2}\)+\(\frac{1}{y^3+3x^2y}\)
2. a phân tích thành nhân tử (x+y)^2-(x+y)-6
b tìm các cặp giá trị (x;y) nguyên thỏa mãn phương trình sau:
2x^2 -x(2y-1)=y+12
1. Áp dụng bất đẳng thức \(\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\) với \(a=x^3+3xy^2,b=y^3+3x^2y\) (a;b > 0)
(Bất đẳng thức này a;b > 0 mới dùng được)
\(A\ge\frac{4}{x^3+3xy^2+y^3+3x^2y}=\frac{4}{\left(x+y\right)^3}\ge\frac{4}{1^3}=4\)
Dấu "=" xảy ra khi: \(\hept{\begin{cases}x^3+3xy^2=y^3+3x^2y\\x+y=1\end{cases}\Leftrightarrow\hept{\begin{cases}x^3-3x^2y+3xy^2-y^3=0\\x+y=1\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(x-y\right)^3=0\\x+y=1\end{cases}}\Leftrightarrow x=y=\frac{1}{2}\)
Đúng 0
Bình luận (0)
TÍNH GIÁ TRỊ CỦA ĐA THỨC SAU BIẾT: x+y=0
\(A=2x+2y+3xy\left(x+y\right)+5\left(x^3y^2+x^2y^3\right)+2\)
\(B=3xy\left(x+y\right)+2x^3y+2x^2y^2+5\)
A=2(x+y)+3xy(x+y)+5x2y2(x+y)+2
A=2.0+3xy.0+5x2y2.0+2
A=2
B=xy(x+y)+2x2y (x+y)+5
B=xy.0+2x2y.0+5=5
Đúng 1
Bình luận (0)
a,Ta có 2(x+y)+3xy(x+y)+5x2y2(x+y)+4
Xg thay x+y=0 vào là dc bn nhó
Chúc bn hok tốt
A=x^3+3^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3 Thu gọn Tìm bậc Tìm giá trị A tạ x =-2,y=1/2
A=2y^3
Bậc là 3
Khi y=1/2 thì A=2*1/8=1/4
Đúng 0
Bình luận (0)
Xét các số thực dương thỏa mãn
log
3
1
-
x
y
x
+
2
y
3
x
y
+
x
+
2
y
-
4
. Tìm giá trị nhỏ nhất Smin của S x + y A.
S
m
i...
Đọc tiếp
Xét các số thực dương thỏa mãn log 3 1 - x y x + 2 y = 3 x y + x + 2 y - 4 . Tìm giá trị nhỏ nhất Smin của S = x + y
A. S m i n = 9 11 9 - 1
B. S m i n = 9 11 - 9 9
C. S m i n = 2 11 - 9 9
D. Đáp án khác
tìm giá trị nguyên của x,y biết: 3xy+x-y=1
<=>9xy+3x-3y=3
<=>3x(y+1)-3(y+1)=0
<=>(y+1)(3x-3)=0
<=>y+1=0<=>y=-1
3x-3=0<=>x=1
Đúng 0
Bình luận (0)
ta có 3xy+x-y=1
<=> 3xy +x-y-1=0
<=> 3xy=0 và x-y-1=0
giải hệ hai phương trình cta được
th1 : x=0 => y= -1
th2: y=0 => x=1
vậy pt cho có 2 cặp nghiệm
Đúng 0
Bình luận (0)
ta có 3xy+x-y=1
<=> 3xy +x-y-1=0
<=> 3xy=0 và x-y-1=0
giải hệ hai phương trình cta được th1 :
x=0 => y= -1 th2: y=0 => x=1
vậy pt cho có 2 cặp nghiệm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời