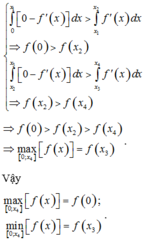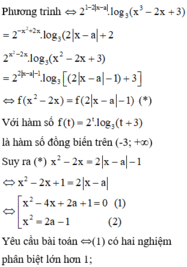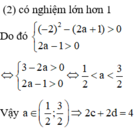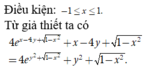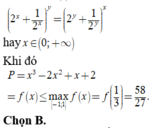tổng các giá trị x thỏa mãn : x5=x4+x3+x2+x+2 là
DP
Những câu hỏi liên quan
Bài 1 : Cho a,b,c là các số hữu tỉ khác 0 sao cho a+b-c/c=a-b+c/b=(-a)+b+c/a
Tính giá trị của biểu thức A=(a+b).(b+c).(c+a)/abc
(LƯU Ý : DẤU / LÀ ...TRÊN.....)
Bài 2 : Cho x,x2,x3,x4,x5,x6 thỏa mãn :
(x2)^2=x1.x3
(x3)^2=x2.x4
(x4)^2=x3.x5
(x5)^2=x4.x6
Chứng minh rằng : x1/x6=(x1+x2+x3+x4+x5/x2+x3+x4+x5+x6)^5
Giusp mk vs nhé các bn !!!
1. cho 6 số khác 0 x1,x2,x3,x4,x5,x6 thỏa mãn điều kiện
x2 mũ 3 = x1.x3, x3 mũ 2 =x2.x4
x4 mũ 2 = x3.x5 , x5 mũ 2 = x4.x6
Cho các số thực
x
1
,
x
2
,
x
3
,
x
4
thỏa mãn
0
x
1
x
2
x
3
x
4
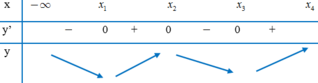
và hàm số yf(x). Biết hàm số yf’(x) có đồ thị như hình vẽ. Gọi M và m lần...
Đọc tiếp
Cho các số thực x 1 , x 2 , x 3 , x 4 thỏa mãn 0 < x 1 < x 2 < x 3 < x 4 và hàm số y=f(x). Biết hàm số y=f’(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn 0 ; x 4 . Đáp áp nào sau đây đúng?
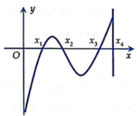
A. M + m = f 0 + f x 3 .
B. M + m = f x 3 + f x 4 .
C. M + m = f x 1 + f x 2 .
D. M + m = f 0 + f x 1 .
Giả sử đa thức
P
(
x
)
x
5
-
a
x
4
+
b
có năm nghiệm
x
1
;
x
2
;
x
3
;
x
4
;
x
5
Đặt
f
(
x
)...
Đọc tiếp
Giả sử đa thức P ( x ) = x 5 - a x 4 + b có năm nghiệm x 1 ; x 2 ; x 3 ; x 4 ; x 5 Đặt f ( x ) = x 2 - 4 Tìm giá trị nhỏ nhất của P = f ( x 1 ) f ( x 2 ) f ( x 3 ) f ( x 4 ) f ( x 5 )
A. 512
B. -512
C. 1024
D. -1024
Cho x1, x2, x3, x4, x5, x6 là các số đôi một khác nhau thuộc tập {1, 2, 3, 4, 5, 6} và thỏa mãn x1-5x2+10x3-10x4+5x5-x6=0. Hỏi có bao nhiêu cách chọn bộ (x1, x2, x3, x4, x5, x6)?
Cho phương trình
4
-
x
-
a
.
log
3
x
2
-
2
x
+
3
+
2
-
x...
Đọc tiếp
Cho phương trình 4 - x - a . log 3 x 2 - 2 x + 3 + 2 - x 2 + 2 x . log 1 3 2 x - a + 2 = 0 . Tập tất cả các giá trị của tham số a để phương trình có 4 nghiệm x 1 ; x 2 ; x 3 ; x 4 thỏa mãn là (c;d). Khi đó giá trị biểu thức T = 2 c + 2 d bằng:
A. 5
B. 2
C. 3
D. 4
Cho 2 hai số thực x, y thỏa mãn
e
x
-
4
y
+
1
-
x
2
-
e
y
2
+
1
-
x...
Đọc tiếp
Cho 2 hai số thực x, y thỏa mãn e x - 4 y + 1 - x 2 - e y 2 + 1 - x 2 - y = y 2 - x 4 . Giá trị lớn nhất của biểu thức P = x 3 + 2 y 2 - 2 x 2 + 8 y - x + 2 bằng
A. 2
B. 58 27
C. 115 27
D. 122 27
BT2: Thực Hiện các phép tính , sau đó tính giá trị biểu thức
a) A=(x-2).(x4+2x3+4x2+8x+16) Với x=3 ĐS A=211
b) B=(x+1).(x7-x6+x5-x4+x3-x2+x-1) Với x=2 ĐS B=255
a: A=x^5-32
Khi x=3 thì A=3^5-32=243-32=211
b: B=x^8-x^7+x^6-x^5+x^4-x^3+x^2-x+x^7-x^6+x^5-x^4+x^3-x^2+x-1
=x^8-1
=2^8-1=255
Đúng 0
Bình luận (0)
1. Cho đa thức f(x)ϵZ[x]f(x)ϵZ[x]f(x)ax4+bx3+cx2+dx+ef(x)ax4+bx3+cx2+dx+e với a, b, c, d, e là các số lẻ.Cm đa thức không có nghiệm hữu tỉ2. Cho P(x) có bậc 3; P(x)ϵZ[x]P(x)ϵZ[x] và P(x) chia hết cho 7 với mọi x ϵZϵZCmR các hệ số của P(x) chia hết cho 7.3. Cho đa thức P(x) bậc 4 có hệ số cao nhất là 1 thỏa mãn P(1)10; P(2)20; P(3)30.Tính P(12)+P(−8)10P(12)+P(−8)104. Tìm đa thức P(x) dạng x5+x4−9x3+ax2+bx+cx5+x4−9x3+ax2+bx+c biết P(x) chia hết cho (x-2)(x+2)(x+3)5. Tìm đa thức bậc 3 có hệ số cao...
Đọc tiếp
1. Cho đa thức f(x)ϵZ[x]f(x)ϵZ[x]
f(x)=ax4+bx3+cx2+dx+ef(x)=ax4+bx3+cx2+dx+e với a, b, c, d, e là các số lẻ.
Cm đa thức không có nghiệm hữu tỉ
2. Cho P(x) có bậc 3; P(x)ϵZ[x]P(x)ϵZ[x] và P(x) chia hết cho 7 với mọi x ϵZϵZ
CmR các hệ số của P(x) chia hết cho 7.
3. Cho đa thức P(x) bậc 4 có hệ số cao nhất là 1 thỏa mãn P(1)=10; P(2)=20; P(3)=30.
Tính P(12)+P(−8)10P(12)+P(−8)10
4. Tìm đa thức P(x) dạng x5+x4−9x3+ax2+bx+cx5+x4−9x3+ax2+bx+c biết P(x) chia hết cho (x-2)(x+2)(x+3)
5. Tìm đa thức bậc 3 có hệ số cao nhất là 1 sao cho P(1)=1; P(2)=2; P(3)=3
6. Cho đa thức P(x) có bậc 6 có P(x)=P(-1); P(2)=P(-2); P(3)=P(-3). CmR: P(x)=P(-x) với mọi x
7. Cho đa thức P(x)=−x5+x2+1P(x)=−x5+x2+1 có 5 nghiệm. Đặt Q(x)=x2−2.Q(x)=x2−2.
Tính A=Q(x1).Q(x2).Q(x3).Q(x4).Q(x5)A=Q(x1).Q(x2).Q(x3).Q(x4).Q(x5) (x1,x2,x3,x4,x5x1,x2,x3,x4,x5 là các nghiệm của P(x))
123456
Tính giá trị của biểu thức sau khi x = 2; y = –2
C = x.(x2 – y).(x3 – 2y2).(x4 – 3y3).(x5 – 4y4).(x6 – 5y5)