mọi người giúp em với !
em xin cảm ơn ạ
Mọi người giúp em bài 9 với ạ em xin cảm ơn!

9:
a: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x< >1\end{matrix}\right.\)
\(P=\dfrac{x+2+\sqrt{x}\left(\sqrt{x}-1\right)-\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}:\dfrac{\sqrt{x}-1}{2}\)
\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\cdot\dfrac{2}{x+\sqrt{x}+1}\)
b: \(x+\sqrt{x}+1=\sqrt{x}\left(\sqrt{x}+1\right)+1>=1>0\)
2>0
Do đó: \(P=\dfrac{2}{x+\sqrt{x}+1}>0\forall x\ne1\)
Mọi người giúp em với ạ, nếu đc thù em xin cả cách giải, em đang cần gấp lắm ạ, cảm ơn mọi người nhiều


Câu 1: A
Câu 2: B
Câu 3: D
Câu 4: A
Câu 5: C
Câu 6: B
Câu 7: A
Câu 9: B
Cần gấp ạ, xin mọi người giúp em vs ạ. Em cảm ơn mọi người. Nếu đc em xin cả cách giải ạ


Hướng dẫn: A đạt GTLN khi \(\dfrac{1}{A}\) đạt GTNN
Ta có: \(x^2+2\ge0\forall x\)
\(\Rightarrow A=\dfrac{1}{x^2+2}\le\dfrac{1}{2}\forall x\)
Vậy GTLN của A là 1/2
=> A
Câu 2: B đạt GTLN khi và chỉ khi x2 đạt giá trị nhỏ nhất
⇔ x2=0 ⇒B = 10 - 0= 0
Chọn đáp án B nhe
Câu 3: Có A= 4x - 2x2= (-2x2 + 4x - 1) + 1=\(-2\left(x^2-2x+1\right)+1\)
⇔ A= \(-2\left(x-1\right)^2+1\le1\)
Chọn đáp án B nha
Nhờ mọi người giúp vs, em đg cần gấp ạ, cho em xin cả cách giải với ạ. Em cảm ơn mọ người


Mọi người giả giúp em với ạ e xin cảm ơn. chi tiết với ạ
b: ĐKXĐ: x>=2/3
PT=>(x-1)(x-2)+(x-1)*căn 3x-2=0
=>căn 3x-2+x-2=0
=>căn 3x-2=-x+2
=>x<=2 và 3x-2=x^2-4x+4
=>x^2-4x+4-3x+2=0 và x<=2
=>x=1
c: =>x+3+x-4-2căn (x^2-x-12)=1
=>2*căn x^2-x-12=2x-1-1=2x-2
=>căn x^2-x-12=x-1
=>x>=1 và x^2-x-12=x^2-2x+1
=>x=13
Em đang cần gấp nên mong mọi người giúp với ạ em xin cảm ơn
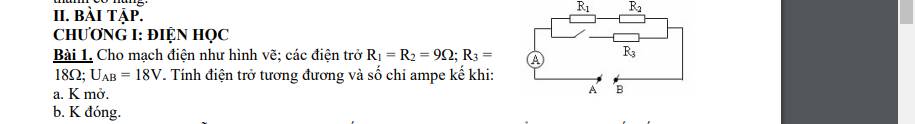 Mọi người giúp em câu hỏi này với ạ! Em xin chân thành cảm ơn!
Mọi người giúp em câu hỏi này với ạ! Em xin chân thành cảm ơn!
a. K mở
\(R_{tđ}=R_1+R_2=9+9=18\Omega\\ I=\dfrac{U}{R_{tđ}}=\dfrac{18}{18}=1A\)
b. K đóng
\(R_{tđ}=\dfrac{\left(R_1+R_2\right).R_3}{R_1+R_2+R_3}=\dfrac{\left(9+9\right)18}{9+9+18}=9\Omega\\ I=\dfrac{U}{R_{tđ}}=\dfrac{18}{9}=2A\)
Mọi người giúp e với giải giúp em câu 2 và câu 3 ạ em xin cảm ơn 
GIÚP EM BÀI TẬP TOÁN 9VỚI Ạ .EM ĐANG KIỂM TRa.CỨU EM VỚI MỌI Người.!!
Em xin cảm ơn rất nhiều luôn ạ
Câu 5:
\(x=\dfrac{6^2}{10}=3.6\left(cm\right)\)
y=10-3,6=6,4(cm)
Có ai ko giúp em với . Em đang cần rất gấp trước 3h00 ạ . Em mong mọi người giúp em . Em xin cảm ơn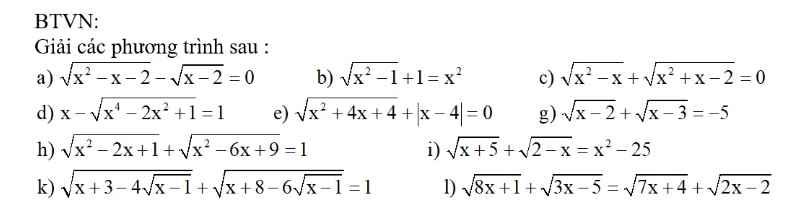
a) ĐKXĐ: \(\left\{{}\begin{matrix}x\le-1\\x\ge2\end{matrix}\right.\)
\(\sqrt{x^2-x-2}-\sqrt{x-2}=0\\ \Leftrightarrow\sqrt{x^2-x-2}=\sqrt{x-2}\\ \Leftrightarrow x^2-x-2=x-2\\ \Leftrightarrow x^2-2x=0\\ \Leftrightarrow x\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=2\left(tm\right)\end{matrix}\right.\)
\(a,ĐK:x\ge2\\ PT\Leftrightarrow x^2-x-2=x-2\\ \Leftrightarrow x^2-2x=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=0\left(ktm\right)\end{matrix}\right.\Leftrightarrow x=2\\ b,ĐK:\left[{}\begin{matrix}x\le-1\\x\ge1\end{matrix}\right.\\ PT\Leftrightarrow\sqrt{x^2-1}=x^2-1\\ \Leftrightarrow x^2-1=\left(x^2-1\right)^2\\ \Leftrightarrow\left(x^2-1\right)\left(x^2-1-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=-1\left(tm\right)\\x=\sqrt{2}\left(tm\right)\\x=-\sqrt{2}\left(tm\right)\end{matrix}\right.\)
\(c,ĐK:\left[{}\begin{matrix}x\le-2\\x\ge1\end{matrix}\right.\\ PT\Leftrightarrow\sqrt{x^2-x}=-\sqrt{x^2+x-2}\\ \Leftrightarrow x^2-x=x^2+x-2\\ \Leftrightarrow2x=2\\ \Leftrightarrow x=1\left(tm\right)\)
\(d,ĐK:x\ge1\\ PT\Leftrightarrow\sqrt{\left(x^2-1\right)^2}=x-1\\ \Leftrightarrow\left|x^2-1\right|=x-1\\ \Leftrightarrow\left[{}\begin{matrix}x^2-1=x-1\left(x\le-1;x\ge1\right)\\x^2-1=1-x\left(-1< x< 1\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x=0\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\\\left[{}\begin{matrix}x=1\left(ktm\right)\\x=-2\left(ktm\right)\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
\(e,PT\Leftrightarrow\left|x+2\right|+\left|x-4\right|=0\Leftrightarrow\left\{{}\begin{matrix}x+2=0\\x-4=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=-2\\x=4\end{matrix}\right.\Leftrightarrow x\in\varnothing\)
\(g,\Leftrightarrow x\in\varnothing\left(\sqrt{x-2}+\sqrt{x-3}\ge0>-5\right)\\ f,\Leftrightarrow\left|x-1\right|+\left|x-3\right|=1\\ \Leftrightarrow\left[{}\begin{matrix}1-x+3-x=1\left(x< 1\right)\\x-1+3-x=1\left(1\le x< 3\right)\\x-1+x-3=1\left(x\ge3\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\left(ktm\right)\\0x=-1\left(ktm\right)\\x=\dfrac{5}{2}\left(ktm\right)\end{matrix}\right.\\ \Leftrightarrow x\in\varnothing\)