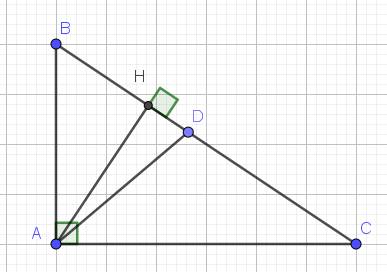
ΔABC vuông tại A có AD là phân giác (D∈BC), DB = 15cm, DC = 20cm. Tính AB, AC, AD
LP
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A.Kẻ phân giác trong AD của BAC ( với D ϵ BC ), biết DB =15cm, DC =20cm. Tính độ dài các đoạn thẳng AB ,AC
ĐS: AB≈ 3,5cm , AC ≈ 4.7 cm
BC=BD+CD
=15+20
=35(cm)
Xét ΔABC có AD là phân giác
nên \(\dfrac{AB}{BD}=\dfrac{AC}{CD}\)
=>\(\dfrac{AB}{15}=\dfrac{AC}{20}\)
=>\(\dfrac{AB}{3}=\dfrac{AC}{4}=k\)
=>AB=3k; AC=4k
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(\left(3k\right)^2+\left(4k\right)^2=35^2\)
=>\(25k^2=35^2\)
=>\(k^2=49\)
=>k=7
=>\(AB=3\cdot7=21\left(cm\right);AC=4\cdot7=28\left(cm\right)\)
Đúng 1
Bình luận (0)
Lời giải:
Theo tính chất đường phân giác:
$\frac{AB}{AC}=\frac{BD}{DC}=\frac{15}{20}=\frac{3}{4}$
$\Rightarrow AB=\frac{3}{4}AC$
Theo định lý Pitago:
$AB^2+AC^2=BC^2=(BD+DC)^2=(15+20)^2=35^2$
$\Rightarrow (\frac{3}{4}AC)^2+AC^2=35^2$
$\Rightarrow AC^2.\frac{25}{16}=35^2$
$\Rightarrow AC^2=784\Rightarrow AC=28$ (cm)
$AB=\frac{3}{4}AC=\frac{3}{4}.28=21$ (cm)
Đúng 0
Bình luận (0)
Đáp số bạn đưa ra chưa đúng.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, AH là đường cao, AD là đường phân giác. Biết AB=15cm; AC=20cm.
a. Tính AC, AH,HB,HC,BD, DC, HD, AD. b. Kẻ HI vuông góc với AB tại I, HK vuông góc với AC tại K. Chứng minh AI.AK.AC. c. Chứng minh tam giác ABC đồng dạng với tam giác AKI. d. Tính diện tích và chu vi tứ giác IBCK.a: BC=căn 15^2+20^2=25cm
AH=15*20/25=12cm
HB=15^2/25=9cm
HC=25-9=16cm
AD là phân giác
=>BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=25/7
=>BD=75/7cm; CD=100/7cm
b: ΔAHB vuông tại H có HI là đường cao
nên AI*AB=AH^2
ΔAHC vuông tại H có HK là đường cao
nên AK*AC=AH^2
=>AI*AB=AK*AC
c: AI*AB=AK*AC
=>AI/AC=AK/AB
=>ΔAIK đồng dạng với ΔACB
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, biết AB=21 cm, AC=28 cm, phân giác AD ( D thuộc BC). Tính độ dài DB, DC. Gọi E là hình chiếu của D trên AC. Hãy tính độ dài DE, EC. Gọi I là giao điểm các đường phân giác và G là trọng tâm của tam giác ABC. Cm IG song song AC ( vẽ hình hộ mình với ạ )
Cho tam giác ABC có AD là tia phân giác của góc A, D thuộc BC. Qua đỉnh B vẽ đường thẳng song song với AC, cắt đường thẳng AD tại điểm E.
a) Chứng minh: Tam giác ABE cân tại B
b)Chứng minh: DB = BE DC AC
c) Chứng minh: DB = AB DC AC
d) Biết AB= 2,5cm; AC= 5cm; DC= 3cm. Tính độ dài đoạn thẳng BD.
Cho tam giác ABC có góc A= 60 độ, AB< AC , đường cao BH ( H thuộc AC)
a) So sánh góc ABC và góc ACB. Tính góc ABH
b) Vẽ AD là phân giác của góc A (D thuộc BC). Vẽ BI vuông góc AD tại I. CMR tam giác AIB= tam giác BHA
c) Tia BI cắt AC ở E. CMR tam giác ABE đều
d) CMR DC> DB
Cho tam giác ABC có AD là tia phân giác của góc A, D thuộc BC. Qua đỉnh B vẽ đường thẳng song song với AC, cắt đường thẳng AD tại điểm E.
a) Chứng minh: Tam giác ABE cân tại B
b)Chứng minh: DB/DC=BE/AC
c) Chứng minh: DB/DC=AB/AC
d) Biết AB= 2,5cm; AC= 5cm; DC= 3cm. Tính độ dài đoạn thẳng BD
a) Ta có : BE // AC
\(\Rightarrow\)^AEB = ^EAC
\(\Rightarrow\)^AEB = ^BAE (= ^EAC)
\(\Rightarrow\)△AEB cân tại B (ĐPCM)
b) Xét △ABC có AD là tia phân giác của góc A
\(\Rightarrow\)\(\frac{DB}{DC}=\frac{AB}{AC}\)
Mà AB = BE (△AEB cân tại B)
\(\Rightarrow\frac{DB}{DC}=\frac{BE}{AC}\)(ĐPCM)
c) Xét △ABC có AD là tia phân giác của góc A
\(\Rightarrow\)\(\frac{DB}{DC}=\frac{AB}{AC}\)(Đã chứng minh ở câu b)
d) Ta có :\(\frac{DB}{DC}=\frac{AB}{AC}\)
\(\Rightarrow\frac{DB}{3}=\frac{2,5}{5}\)
\(\Rightarrow DB=1,5\)
Vậy DB = 1,5 cm
Cho tam giác ABC, vuông tại A, có: AB=16cm, AC=12cm. AD là đường phân giác (D\(\in\)BC)
a) Tính \(\frac{DB}{DC}\)
b) Tính BC, DB, DC
c) Kẻ đường cao AH (H\(\in\)BC) .C/m tam gái CHA đồng dạng với tam gái AHB. Tính\(\frac{Scha}{Sahb}\)
d) Tính Ah
tam giác ABC vuông tại A ,AB bằng 15cm, AC bằng 20cm đường phân giác BD
a) tính AD
b) gọi H là hình chiếu của tam giác trên BC . tính độ dài AH,HB
Lời giải:
a)
Áp dụng định lý Pitago: BC=AB2+AC2−−−−−−−−−−√=25BC=AB2+AC2=25 (cm)
Theo tính chất đường phân giác:
ADDC=ABBC=1525=35ADDC=ABBC=1525=35
⇔ADAD+DC=33+5⇔ADAD+DC=33+5
⇔ADAC=38⇔AD20=38⇒AD=7,5⇔ADAC=38⇔AD20=38⇒AD=7,5 (cm)
b) Ta có: SABC=AH.BC2=AB.AC2SABC=AH.BC2=AB.AC2
⇒AH.BC=AB.AC⇔AH.25=15.20=300⇒AH.BC=AB.AC⇔AH.25=15.20=300
⇒AH=12⇒AH=12 (cm)
Áp dụng định lý Pitago cho tam giác vuông AHBAHB:
BH=AB2−AH2−−−−−−−−−−√=152−122−−−−−−−−√=9BH=AB2−AH2=152−122=9 (cm)
k cho e vs ạ !!!
cj/anh đừng chép bài đó e lm sai rùi
cj/anh theo link này để xem ạ https://h.vn/hoi-dap/tim-kiem?q=1.+Cho+tam+gi%C3%A1c+ABC+vu%C3%B4ng+%E1%BB%9F+A+,+AB=15cm,AC=20cm,+%C4%91%C6%B0%E1%BB%9Dng+ph%C3%A2n+gi%C3%A1c+BD++a,+t%C3%ADnh+%C4%91%E1%BB%99+d%C3%A0i+AD++b,+g%E1%BB%8Di+H+l%C3%A0+h%C3%ACnh+chi%E1%BA%BFu+c%E1%BB%A7a+A+tr%C3%AAn+BC+.+T%C3%ADnh+%C4%91%E1%BB%99+d%C3%A0i+AH,HB++c,+cm+tam+gi%C3%A1c+AID+l%C3%A0+tam+gi%C3%A1c+c%C3%A2n&id=632651
\(GT:\Delta ABC,A=90^O\)
\(AB=15cm\)
\(AC=20cm\)
a,Ta tính được BC = 25cm
\(\frac{DA}{DC}=\frac{AB}{BC}=\frac{15}{25}=\frac{3}{5}\Leftrightarrow\frac{DA}{DA+DC}=\frac{3}{3+5}\)
\(\Rightarrow\frac{DA}{20}=\frac{3}{8}\Rightarrow DA=7,5cm\)
b,\(AH=\frac{AB.AC}{BC}=\frac{15.20}{25}=12cm\)
\(BH=\sqrt{AB^2-AH^2}=\sqrt{15^2-12^2}=9CM\)
Vậy a) AD = 7,5 cm
b)AH = 12 cm ; BH = 9 cm
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A và AB =12cm, AC =16cm .Đường phân giác góc A cắt BC tại D
a) Tính BC ,BD vad CD ĐS: BC =20cm , BD≈8,6cm ,DC≈11,4 cm
b) Vẽ đường cao AH .Tính AH ,HD và AD ĐS: AH ≈9.6 cm , HD ≈1,4cm , AD ≈9,7 cm
Lời giải:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20$ (cm)
Áp dụng tính chất đường phân giác:
$\frac{BD}{DC}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}$
Mà: $BD+DC=BC=20$ nên:
$BD=20:(3+4).3=\frac{60}{7}$ (cm)
$CD= 20:(3+4).4=\frac{80}{7}$ (cm)
b.
$AH=2S_{ABC}:BC=\frac{AB.AC}{BC}=\frac{12.16}{20}=9,6$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-9,6^2}=7,2$ (cm)
$HD = BD-BH = \frac{60}{7}-7,2=\frac{48}{35}$ (cm)
$AD = \sqrt{AH^2+HD^2}=\sqrt{9,6^2+(\frac{48}{35})^2}=\frac{48\sqrt{2}}{7}$ (cm)
Đúng 2
Bình luận (0)
a: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=12^2+16^2=20^2\)
=>\(BC=20\left(cm\right)\)
Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
=>\(\dfrac{BD}{12}=\dfrac{CD}{16}\)
=>\(\dfrac{BD}{3}=\dfrac{CD}{4}\)
mà BD+CD=BC=20
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{20}{7}\)
=>\(BD=\dfrac{20}{7}\cdot3=\dfrac{60}{7}\left(cm\right);CD=\dfrac{20}{7}\cdot4=\dfrac{80}{7}\left(cm\right)\)
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot20=12\cdot16=192\)
=>\(AH=\dfrac{192}{20}=9,6\left(cm\right)\)
Ta có: ΔAHB vuông tại H
=>\(HB^2+AH^2=AB^2\)
=>\(HB^2=12^2-9,6^2=51,84\)
=>\(HB=\sqrt{51,84}=7,2\left(cm\right)\)
=>HC=BC-HB=12,8(cm)
Vì CD<CH
nên D nằm giữa C và H
=>CD+DH=CH
=>\(DH=12.8-\dfrac{80}{7}=\dfrac{48}{35}\left(cm\right)\)
ΔAHD vuông tại H
=>\(AH^2+HD^2=AD^2\)
=>\(AD^2=\left(\dfrac{48}{35}\right)^2+9,6^2=\dfrac{4608}{49}\)
=>\(AD=\sqrt{\dfrac{4608}{49}}=\dfrac{48\sqrt{2}}{7}\left(cm\right)\)
Đúng 1
Bình luận (0)