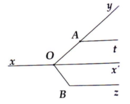
Cho hình vẽ sau đây. Chứng minh rằng OA = OB.
VL
Những câu hỏi liên quan
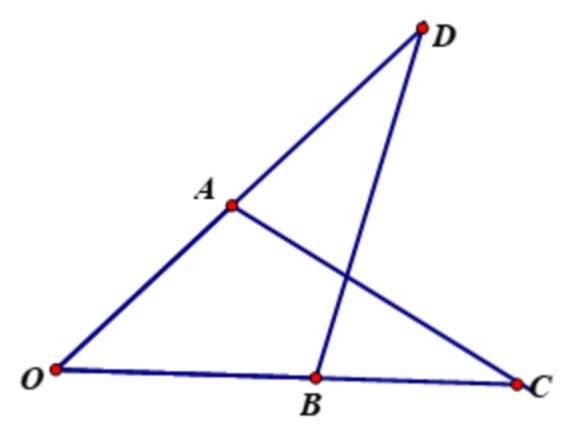
Cho hình vẽ sau, biết OA = OB; góc OAC = góc OBD.
a) Chứng minh rằng AC = BD; OC = OD; AD = BC.
b) Chứng minh rằng tam giác ADC = tam giác BCD.
c) Gọi I là giao điểm của AC và BD. Chứng minh rằng IA = IB và IC = ID.
d) Chứng minh rằng OI là tia phân giác của góc AOB và OI vuông góc CD.
a: Xét ΔOBD và ΔOAC có
\(\widehat{OBD}=\widehat{OAC}\)
OB=OA
\(\widehat{BOD}\) chung
Do đó: ΔOBD=ΔOAC
=>BD=AC; OD=OC
OB+BC=OC
OA+AD=OD
mà OB=OA và OC=OD
nên BC=AD
b: Xét ΔADC và ΔBCD có
AD=BC
CD chung
AC=BD
Do đó: ΔADC=ΔBCD
c: ΔADC=ΔBCD
=>\(\widehat{IDC}=\widehat{ICD}\)
=>ΔIDC cân tại I
=>ID=IC
ID+IB=BD
IC+IA=AC
mà ID=IC và BD=AC
nên IB=IA
d: Xét ΔOAI và ΔOBI có
OA=OB
AI=BI
OI chung
Do đó: ΔOAI=ΔOBI
=>\(\widehat{AOI}=\widehat{BOI}\)
=>OI là phân giác của góc AOB
=>OI là phân giác của góc COD
ΔCOD cân tại O
mà OI là đường phân giác
nên OI\(\perp\)CD
Đúng 1
Bình luận (0)
a, xét tam giác OBD và tam giác OAC có:
góc O chung
OA=OB(gt)
góc OAC= góc OBD(gt)
=>tam giác OBD= tam giác OAC (g.c.g)
=>\(\left\{{}\begin{matrix}AC=BD\\OC=OD\end{matrix}\right.\)(2 cạnh tương ứng)
Đúng 0
Bình luận (1)
b, Nối D với C
Xét tam giác ADC và tam giác BCD có:
AD=BC ( cmt)
BD=AC(cmt)
CD cạnh chung
=>tam giác ADC =tam giác BCD (c.c.c)
Đúng 0
Bình luận (0)
Cho hình bs 7. Chứng minh rằng OA = OB
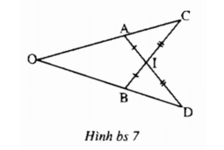
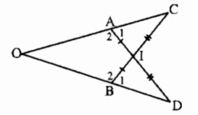
+) Xét ∆AIC và ∆BID có:
AI = BI (giả thiết)
∠AIC = ∠BID ( hai góc đối đỉnh).
IC = ID ( giả thiết)
Suy ra: ∆AIC = ∆BID (c.g.c)
Suy ra: ∠C = ∠D; ∠A1 = ∠B1 (1)
+) Lại có: ∠A1 + ∠A2 = 180º (hai góc kề bù)
Và ∠B1 + ∠B2 = 180º (hai góc kề bù)
Suy ra: ∠A2 = ∠B2
+) Xét tam giác OAD và ∆ OBC có:
∠A2 = ∠B2 (chứng minh trên)
AD = BC (vì AI + ID = BI + IC)
∠D = ∠C (chứng minh trên)
Suy ra: ∆OAD = ∆ OBC (g.c.g)
Suy ra: OA = OB (hai cạnh tương ứng).
Đúng 0
Bình luận (0)
B1: Cho góc bẹt xOy. Trên cùng một nửa mặt phẳng bờ xy, vẽ các tia Om và On sao cho xOmyOn và 90*. Gọi Oz là tia phân giác của góc mOn. Chứng minh rằng Oz _|_ xy.B2: Cho góc AOB 40*. Vẽ tia Oc là tia đối của tia OA. Tính góc COD, biết rằng:a) OD _|_ Ob, các tia Od và OA thuộc hai nửa mặt phẳng đối nhau bờ Obb)OD _|_ Ob, các tia OD và OA thuộc cùng một nửa mặt phẳng bở OBE CẦN GẤP MỌI NGƯỜI GIÚP E VS ẠCÓ HÌNH HOẶC HÌNH MINH HỌA THÌ CÀNG TỐT Ạ
Đọc tiếp
B1: Cho góc bẹt xOy. Trên cùng một nửa mặt phẳng bờ xy, vẽ các tia Om và On sao cho xOm=yOn và <90*. Gọi Oz là tia phân giác của góc mOn. Chứng minh rằng Oz _|_ xy.
B2: Cho góc AOB = 40*. Vẽ tia Oc là tia đối của tia OA. Tính góc COD, biết rằng:
a) OD _|_ Ob, các tia Od và OA thuộc hai nửa mặt phẳng đối nhau bờ Ob
b)OD _|_ Ob, các tia OD và OA thuộc cùng một nửa mặt phẳng bở OB
E CẦN GẤP MỌI NGƯỜI GIÚP E VS Ạ
CÓ HÌNH HOẶC HÌNH MINH HỌA THÌ CÀNG TỐT Ạ
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
Đúng 0
Bình luận (0)
Cho hình vẽ biết a//b Chứng minh OA vuông góc với OB
Cho góc MON = 120 độ , vẽ các tia OA , OB ở trong góc đó sao cho OA vuông góc với OM , OB vuông góc với ON .
Chứng minh rằng góc AON = góc BOM .
theo đề ta có góc MOA bằng 90 độ, góc BON bằng 90 độ
vì tia OA nằm giữa hai tia ON và OM
=>góc AON = góc MOA-góc AON
=>góc AON=120 độ -90 đọ =30 độ
vì tia OB nằm giữa hai tia OM và ON
=> góc BOM = góc MON- góc BON
=> góc BOM= 120 độ - 90 độ
=> góc BOM =30 độ
So sánh AON=BOM( vì 30 độ =30 độ)
Đúng 0
Bình luận (0)
theo đề ta có góc MOA bằng 90 độ, góc BON bằng 90 độ
vì tia OA nằm giữa hai tia ON và OM
=>góc AON = góc MOA-góc AON
=>góc AON=120 độ -90 đọ =30 độ
vì tia OB nằm giữa hai tia OM và ON
=> góc BOM = góc MON- góc BON
=> góc BOM= 120 độ - 90 độ
=> góc BOM =30 độ
So sánh AON=BOM( vì 30 độ =30 độ)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho Ox vuông góc Oy. Trong xOy vẽ hai tia OA; OB sao cho aOx bằng bOy . Vẽ tia OC sao cho Oy là phân giác aOc . 1) Tính số đo aOc . 2) Chứng minh rằng: tia Oy là phân giác bOx . 3) Tia Ob có phải phân giác yOc không? 4) Chứng minh rằng: cOx bằng 90 độ hay Ox vuông góc OC.
Cho hình vẽ bên, biết
y
A
t
^
40
°
,
x
O
y
^
140
°
,
O
B
z
^
130
°
và
O
A
⊥
O
B
. Chứng minh At // Bz.
Đọc tiếp
Cho hình vẽ bên, biết y A t ^ = 40 ° , x O y ^ = 140 ° , O B z ^ = 130 ° và O A ⊥ O B . Chứng minh At // Bz.
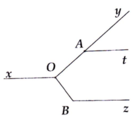
Cho hình vẽ bên, biết
y
A
t
^
40°,
x
O
y
^
140°,
O
B
z
^
130° và OA
⊥
OB. Chứng minh At // Bz
Đọc tiếp
Cho hình vẽ bên, biết y A t ^ = 40°, x O y ^ = 140°, O B z ^ = 130° và OA ⊥ OB. Chứng minh At // Bz
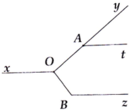
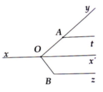 Kẻ tia đối Ox' của Ox =>
y
O
x
'
^
= 40°
Kẻ tia đối Ox' của Ox =>
y
O
x
'
^
= 40°
=> y O x ' ^ = y A t ^ (hai góc đồng vị bằng nhau)
=> Ox' // At (1).
Mặt khác: OA ⊥ OB => A O B ^ = 90 °
=> x ' O B ^ = y O B ^ − y O x ' ^ = 90 ° − 40 ° = 50 °
=> x ' O B ^ = O B z ^ = 50 ° + 130 ° = 180 °
(hai góc trong cùng phía bù nhau)
=>Ox' //Bz (2).
Từ (1) và (2), suy ra At //Bz
Đúng 0
Bình luận (0)
Vẽ hình theo các diễn đạt sau :
Cho góc xOy ( góc nhọn) . Trên tia Ox lấy điểm A , trên tia Oy lấy điểm B . Gọi E là trung điểm của OB , trên tia AE lấy điểm F sao cho : AF = 2.AE
Chứng minh rằng : OA = BF
oeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee
Đúng 0
Bình luận (0)