giúp mik với cảm ơn mn nhiều ạ
CN
Những câu hỏi liên quan
mn giúp mik với ạ, giải chi tiết ra luôn, hôm nay mik phải nộp rùi, cảm ơn mn nhiều ạ

Bài 5:
a, Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)
\(\sin B=\dfrac{AC}{BC}=\dfrac{3}{5}\approx\sin37^0\\ \Rightarrow\widehat{B}\approx37^0\\ \Rightarrow\widehat{C}\approx90^0-37^0=53^0\)
b, Áp dụng HTL: \(S_{AHC}=\dfrac{1}{2}AH\cdot HC=\dfrac{1}{2}\cdot\dfrac{AB\cdot AC}{BC}\cdot\dfrac{AC^2}{BC}=\dfrac{1}{2}\cdot\dfrac{12}{5}\cdot\dfrac{9}{5}=\dfrac{54}{25}\left(cm^2\right)\)
c, Vì AD là p/g nên \(\dfrac{DH}{DB}=\dfrac{AH}{AB}\)
Mà \(AC^2=CH\cdot BC\Leftrightarrow\dfrac{HC}{AC}=\dfrac{AC}{BC}\)
Mà \(AH\cdot BC=AB\cdot AC\Leftrightarrow\dfrac{AH}{AB}=\dfrac{AC}{BC}\)
Vậy \(\dfrac{DH}{DB}=\dfrac{HC}{AC}\)
Đúng 2
Bình luận (1)
Các bn giúp mik với, mik cần gấp ạ!!!Cảm ơn mn nhiều
Đọc tiếp
Các bn giúp mik với, mik cần gấp ạ!!!
Cảm ơn mn nhiều ![]()
![]()
a) Xét \(\Delta BAD\) và \(\Delta BCE:\)
\(\widehat{B}chung.\)
\(\widehat{D}=\widehat{E}\left(=90^o\right).\)
\(\Rightarrow\Delta BAD\sim\Delta BCE\left(g-g\right).\)
b) Xét \(\Delta ABC:\)
CE là đường cao \(\left(CE\perp AB\right).\)
AD là đường cao \(\left(AD\perp BC\right).\)
Mà F là giao điểm của CE và AD.
\(\Rightarrow BF\) là đường cao.
Xét \(\Delta ABC\) cân tại B:
BF là đường cao (gt).
\(\Rightarrow BF\) là phân giác \(\widehat{ABC}.\)
Đúng 1
Bình luận (1)
Mn ơi giúp mình với ạ, mik cảm ơn rất nhiều luôn ạ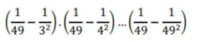
\(=\left(\dfrac{1}{49}-\dfrac{1}{9}\right)\cdot...\cdot\left(\dfrac{1}{49}-\dfrac{1}{49}\right)\cdot...\cdot\left(\dfrac{1}{49}-\dfrac{1}{49^2}\right)=0\)
Đúng 1
Bình luận (0)
Dạ mn giúp mik làm bài bài với ạ sẵn tiện mn kiểm tra xem có chỗ nào sai ko r giúp sửa lại với ạ mik cảm ơn nhiều
mn giúp mik với,mk đang cần rất gấp ạ! Cảm ơn mn rất nhiều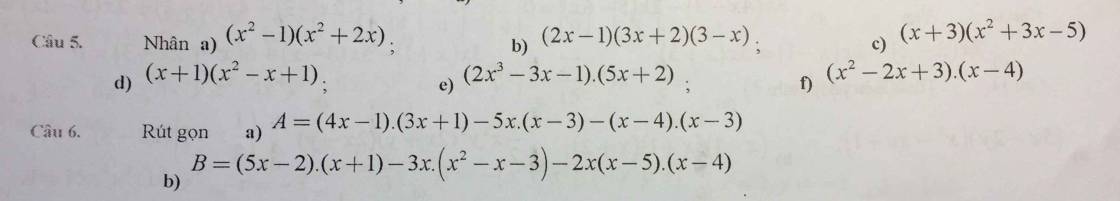
Câu 6:
a: =12x^2+4x-3x-1-5x^2+15x-x^2+7x-12
=6x^2+23x-13
b: =5x^2+5x-2x-2-3x^3+3x^2+9x-2x(x^2-9x+20)
=-3x^3+8x^2+14x-2-2x^3+18x^2-40x
=-5x^3+26x^2-26x-2
Đúng 0
Bình luận (0)
Mn giải giúp mik câu 2 và phần b câu 3 với ạ . Cảm ơn mn nhiều
Câu 2:
Ta có: \(x^2-2\left(m+1\right)x+m^2+4=0\)
a=1; b=-2m-2; \(c=m^2+4\)
\(\text{Δ}=b^2-4ac\)
\(=\left(-2m-2\right)^2-4\cdot\left(m^2+4\right)\)
\(=4m^2+8m+4-4m^2-16\)
=8m-12
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow8m>12\)
hay \(m>\dfrac{3}{2}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)=2m+2\\x_1x_2=m^2+4\end{matrix}\right.\)
Vì x1 là nghiệm của phương trình nên ta có:
\(x_1^2-2\left(m+1\right)\cdot x_1+m^2+4=0\)
\(\Leftrightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)
Ta có: \(x_1^2+2\left(m+1\right)x_2=2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2-2m^2-20=0\)
\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)-3m^2-24=0\)
\(\Leftrightarrow2\left(m+1\right)\cdot\left(2m+2\right)-3m^2-24=0\)
\(\Leftrightarrow4m^2+8m+4-3m^2-24=0\)
\(\Leftrightarrow m^2+8m-20=0\)
Đến đây bạn tự tìm m là xong rồi
Đúng 1
Bình luận (1)
Giúp mik với ạ,em đang cần gấp lắm cảm ơn mn nhiều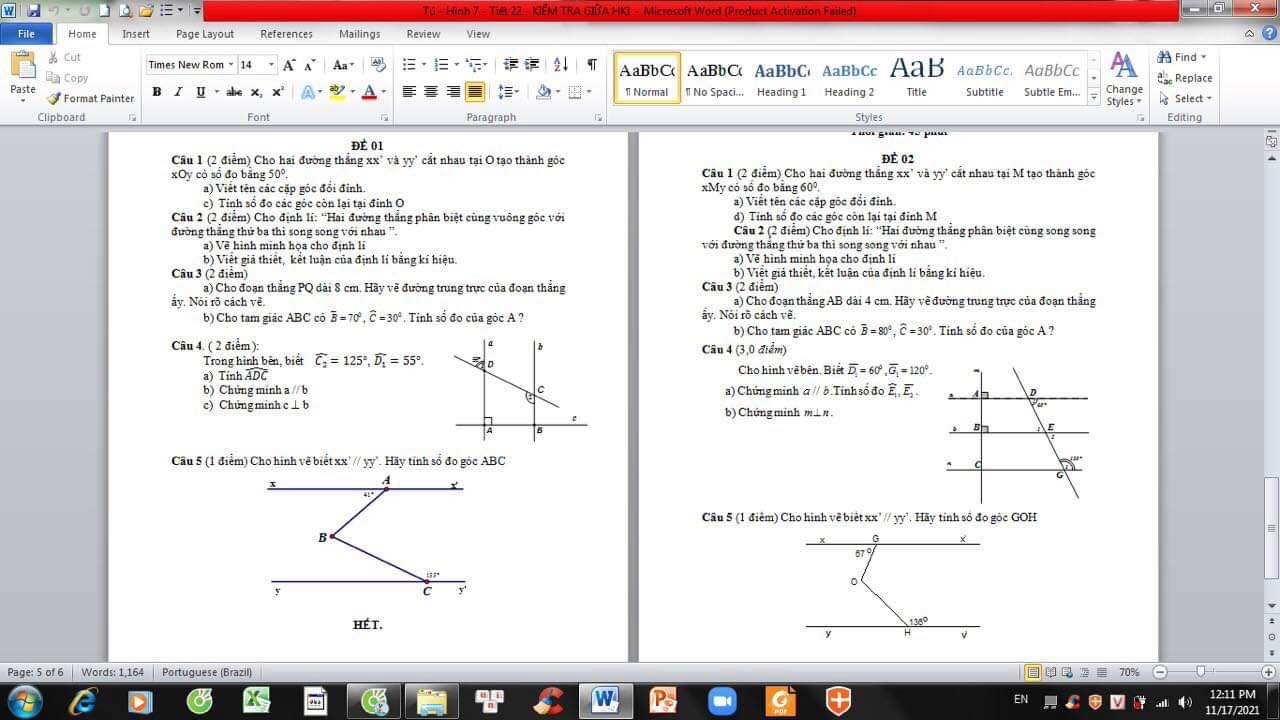
Bạn cần hỗ trợ bài nào thì nên chụp nguyên bài đó ra thôi. Nếu bạn cần giúp nhiều bài thì nên tách lẻ mỗi bài mỗi post hoặc 2 bài/ post. Bạn chụp như thế này gây "ngợp" nên sẽ ít ai dừng lại và hỗ trợ.
Đúng 0
Bình luận (0)
Dạ mọi người giúp mik bài này với ạ sẵn tiện mọi người kiểm tra xem có chỗ nào mik làm sai thì mn sửa giúp mik với ạ mik cảm ơn nhiều ạ 🙆♀️❤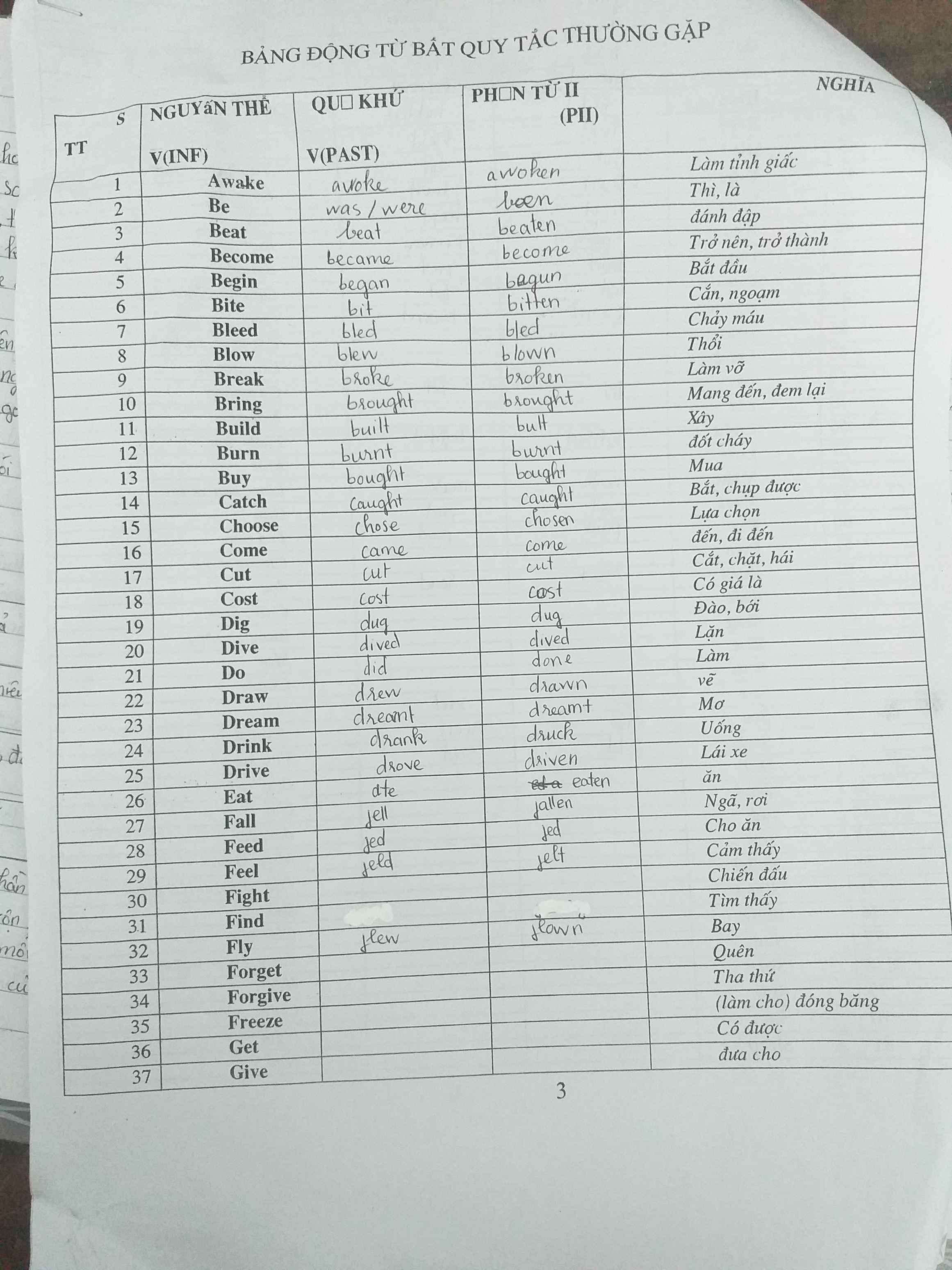
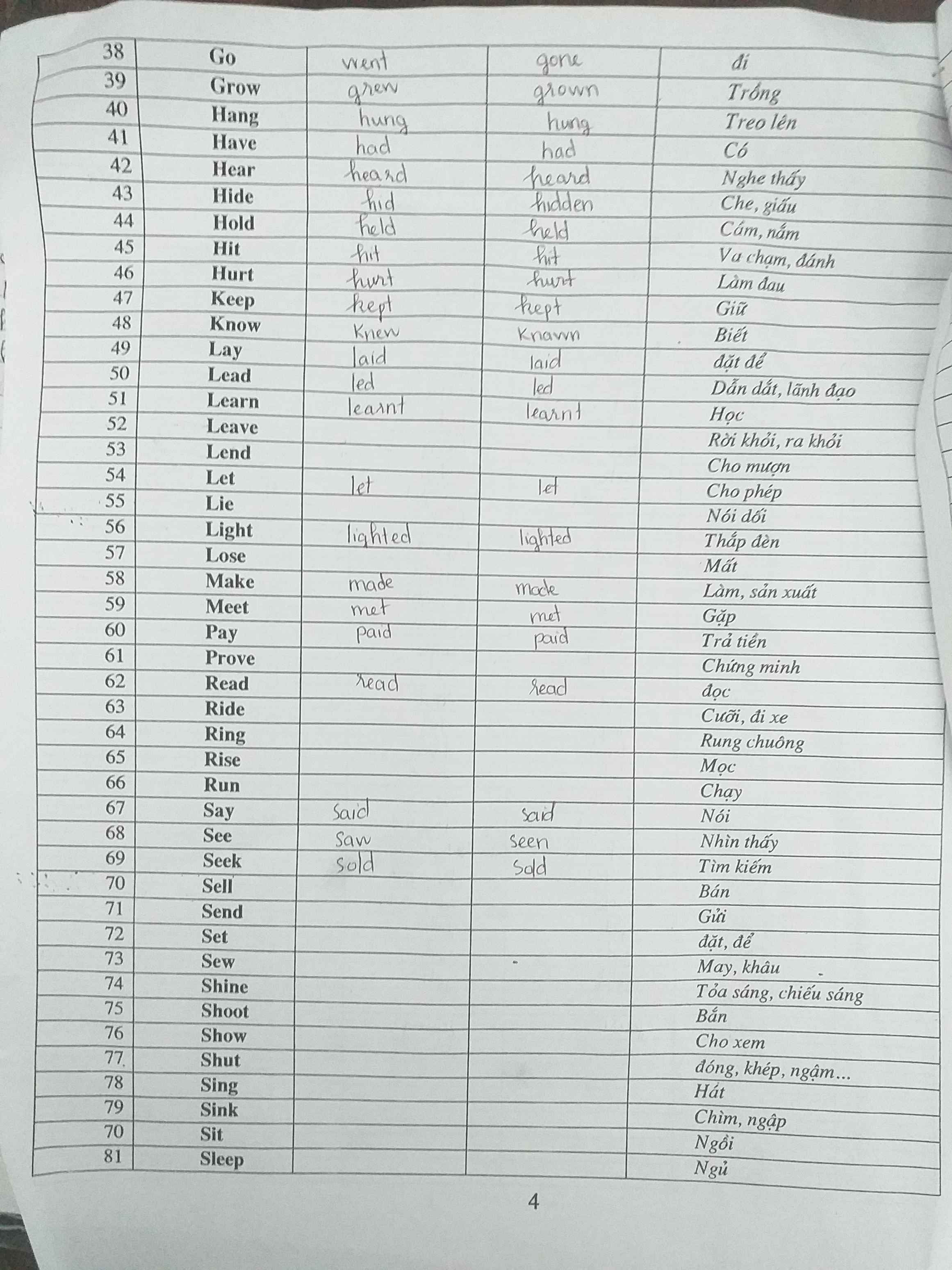

của bạn nè.Mik lớp 5 nhưng vẫn phải học thuộc hết



Xem thêm câu trả lời
mn giúp mik vs ạ mik cảm ơn nhiều :)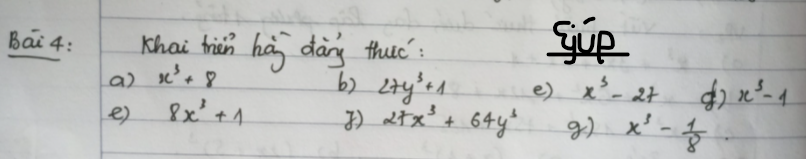
a: \(x^3+8=\left(x+2\right)\left(x^2-2x+4\right)\)
b: \(27y^3+1=\left(3y+1\right)\left(9y^2-3y+1\right)\)
c: \(x^3-27=\left(x-3\right)\left(x^2+3x+9\right)\)
d: \(x^3-1=\left(x-1\right)\left(x^2+x+1\right)\)
e: \(8x^3+1=\left(2x+1\right)\left(4x^2-2x+1\right)\)
f: \(27x^3+64y^3=\left(3x+4y\right)\left(9x^2-12xy+16y^2\right)\)
g: \(x^3-\dfrac{1}{8}=\left(x-\dfrac{1}{2}\right)\left(x^2+\dfrac{1}{2}x+\dfrac{1}{4}\right)\)
Đúng 2
Bình luận (1)



