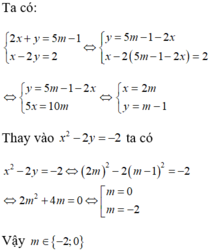Cho hệ phương trình {2x+y=5m-1 ; x-2y=2 (m là tham số)
a) Giải hệ phương trình với m=1
b) Tìm m để hệ phương trình có nghiệm(x,y)thỏa mãn x\(^2\)-2y\(^2\)=1
NN
Những câu hỏi liên quan
Cho hệ phương trình:\(\left\{{}\begin{matrix}2x+y=5m-1\\x-2y=2\end{matrix}\right.\)(m là tham số)
1.Giải hệ phương trình với m=1
2.Tìm m để hệ phương trình có nghiệm (x;y) thỏa mãn đẳng thức \(x^2+2y^2=2\)
Linh tinh đếyyy ạ. Có gì sai thông cảm nhaaaa
Đúng 1
Bình luận (0)
Cho hệ phương trình: \(\hept{\begin{cases}x+y=5m-8\\2x-3y=9-5m\end{cases}}\)
a, Giải hệ phương trình với m = 1.
b, Tìm m để hệ có nghiệm ( x;y) thỏa mãn: \(x+y=xy+13\)
Cho hệ phương trình
2
x
+
y
5
m
−
1
x
−
2
y
2
. Có bao nhiêu g...
Đọc tiếp
Cho hệ phương trình 2 x + y = 5 m − 1 x − 2 y = 2 . Có bao nhiêu giá trị của m để hệ phương trình có nghiệm thỏa mãn x 2 – 2 y 2 = − 2
A. 0
B. 1
C. 2
D. 3
Ta có 2 x + y = 5 m − 1 x − 2 y = 2
⇔ y = 5 m − 1 − 2 x x − 2 5 m − 1 − 2 x = 2 ⇔ y = 5 m − 1 − 2 x 5 x = 10 m
⇔ x = 2 m y = m − 1
Thay vào x 2 – 2 y 2 = − 2 ta có
x 2 – 2 y 2 = − 2 ⇔ ( 2 m 2 ) – 2 ( m − 1 ) 2 = − 2 ⇔ 2 m 2 + 4 m = 0 ⇔ m = 0 m = − 2
Vậy m ∈ {−2; 0}
Đáp án: C
Đúng 0
Bình luận (0)
Cho hệ phương trình
2
x
+
y
5
m
-
1
x
-
2
y
2
. Có bao nhiêu giá trị của m để hệ phương trình có nghiệm thỏa mãn:...
Đọc tiếp
Cho hệ phương trình 2 x + y = 5 m - 1 x - 2 y = 2 . Có bao nhiêu giá trị của m để hệ phương trình có nghiệm thỏa mãn: x 2 - 2y = -2
A. 0
B. 1
C. 2
D. 3
Cho hệ phương trình {2x + y = 5m -1 và x - 2y=2 a) Giải HPT với m = 1 b) Tìm m để HPT có nghiệm ( x ; y) thoả mãn 2x - y = 3
Cho hệ phương trình
2
x
+
3
y
7
2
−
m
4
x
−
y
5...
Đọc tiếp
Cho hệ phương trình 2 x + 3 y = 7 2 − m 4 x − y = 5 m . Có bao nhiêu giá trị của m mà m > 1 2 để hệ phương trình có nghiệm thỏa mãn: x 2 + 2 y 2 = 25 16
A. 0
B. 1
C. 2
D. 3
Ta có
2 x + 3 y = 7 2 − m 4 x − y = 5 m ⇔ 4 x + 6 y = 7 − 2 m 4 x − y = 5 m ⇔ 7 y = 7 − 7 m 4 x − y = 5 m ⇔ y = 1 − m 4 x − 1 − m = 5 m ⇔ y = 1 − m x = 4 m + 1 4
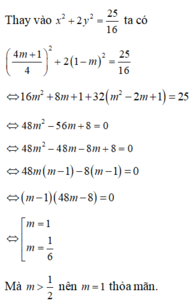
Đáp án: B
Đúng 0
Bình luận (0)
Cho hệ phương trình \(\left\{{}\begin{matrix}x-y=4\\2x+3y=5m+3\end{matrix}\right.\). Tìm \(m\) để hệ phương trình có nghiệm \(\left(x;y\right)\) sao cho biểu thức \(A=\dfrac{2019}{x^2+y^2-4}\) đạt giá trị lớn nhất.
=>2x-2y=8 và 2x+3y=5m+3
=>-5y=8-5m-3=-5m+5 và x-y=4
=>y=m-1 và x=4+m-1=m+3
x^2+y^2-4=(m+3)^2+(m-1)^2-4
=m^2+6m+9+m^2-2m+1-4
=2m^2+4m+6
=2(m^2+2m+3)
=2(m^2+2m+1+2)
=2[(m+1)^2+2]>=4
=>A<=2019/4
Dấu = xảy ra khi m=-1
Đúng 0
Bình luận (0)
Cho hệ phương trình: \(\hept{\begin{cases}2x+y=5m-6\\x-2y=2\end{cases}}\) (m là tham số)
Tìm m để hệ phương trình có nghiệm (x;y) thoả mãn: \(2x^2-y^2=4\)
\(\hept{\begin{cases}2x+y=5m-6\\x-2y=2\end{cases}\Leftrightarrow\hept{\begin{cases}2x+y=5m-6\\2x-4y=4\end{cases}\Leftrightarrow}\hept{\begin{cases}5y=5m-10\\x-2y=2\end{cases}}}\)
\(\left(1\right)\Rightarrow y=\frac{5m-10}{5}=m-2\)
Thay vào phương trình (2) ta được :
\(x-2\left(m-2\right)=2\Leftrightarrow x=2+2m-4=2m-2\)
Vậy hệ phương trình có nghiệm ( x ; y ) = ( 2m - 2 ; m - 2 ) (*)
Thay (*) vào biểu thức trên ta được :
\(2\left(2m-2\right)^2-\left(m-2\right)^2=4\)
\(\Leftrightarrow2\left(4m^2-8m+4\right)-m^2+4m-4=4\)
\(\Leftrightarrow8m^2-16m+8-m^2+4m-4=4\)
\(\Leftrightarrow7m^2-12m=0\Leftrightarrow m\left(7m-12\right)=0\Leftrightarrow m=0;m=\frac{12}{7}\)
\(\hept{\begin{cases}2x+y=5m-6\\2x-4y=4\end{cases}}\)
\(5y=5m-10\)
\(y=m-2\)
\(\hept{\begin{cases}2x+y=5m-6\\2x-4y=4\end{cases}< =>\hept{\begin{cases}2x+\left(m-2\right)=5m-6\\2x-4\left(m-2\right)=4\end{cases}}}\)
\(< =>x-2\left(m-2\right)=2\)
\(x-2m+4=2\)
\(x=2m-2\)
\(< =>2x^2-y^2=4\)
\(2\left(4m^2-8m+4\right)-\left(m^2-4m+4\right)\)
\(8m^2-16m+8-m^2+4m-4-4=0\)
\(7m^2-12m=0\)
\(m\left(7m-12\right)=0\)
\(\orbr{\begin{cases}m=0\\m=\frac{12}{7}\end{cases}}\)
Giá trị của tham số m để hệ phương trình 2x -y= 5m + 1 x+y = m-4 có nghiệm duy nhất (x;y) thoả mãn -x-y< 0
Tìm m để hệ phương trình \(\left\{{}\begin{matrix}x+2y=5m-1\\-2x+y=2\end{matrix}\right.\) có nghiệm (x;y) thoả mãn \(\sqrt{x}+\sqrt{y}=\sqrt{2}\)
Helppp meee!
\(\left\{{}\begin{matrix}x+2y=5m-1\\-2x+y=2\end{matrix}\right.< =>\left\{{}\begin{matrix}2x+4y=10m-2\\-2x+y=2\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}5y=10m\\-2x+y=2\end{matrix}\right.< =>\left\{{}\begin{matrix}y=2m\\x=m-1\end{matrix}\right.\)
=>\(\sqrt{x}+\sqrt{y}=\sqrt{2}\left(1\right)\)
=>\(\sqrt{m-1}+\sqrt{2m}=\sqrt{2}\) (\(m\ge1\))
\(< =>\left(\sqrt{m-1}\right)^2=|\left(\sqrt{2}-\sqrt{2m}\right)^2|\)
<=>\(m-1=\left[\sqrt{2}.\left(1-\sqrt{m}\right)\right]^2< =>m-1=|2.\left(1-\sqrt{m}\right)^2|\)
<=>\(m-1=|2\left(1-2\sqrt{m}+m\right)|=\left|2-4\sqrt{m}+2m\right|\)
với \(\left|2-4\sqrt{m}+2m\right|=2-4\sqrt{m}+2m< =>m\le1\)
ta có pt:
<=>\(m-1-2+4\sqrt{m}-2m=0\)
\(< =>-m+4\sqrt{m}-3=0< =>-\left(m-4\sqrt{m}+3\right)=0\)
<=>\(m-4\sqrt{m}+3=0< =>\left(\sqrt{m}-3\right)\left(\sqrt{m}-1\right)=0\)
<=>\(\left[{}\begin{matrix}\sqrt{m}-3=0\\\sqrt{m}-1=0\end{matrix}\right.< =>\left[{}\begin{matrix}m=9\left(loai\right)\\m=1\left(TM\right)\end{matrix}\right.\)
nếu \(|2-4\sqrt{m}+2m|=-2+4\sqrt{m}-2m< =>m\ge1\)
=>\(-2+4\sqrt{m}-2m=m-1< =>3m-4\sqrt{m}+1=0\)
<=>\(3\left(m-2.\dfrac{2}{3}\sqrt{m}+\dfrac{1}{3}\right)=3\left(m-2.\dfrac{2}{3}\sqrt{m}+\dfrac{4}{9}-\dfrac{4}{9}+\dfrac{1}{3}\right)=0\)
<=>\(\left(\sqrt{m}-1\right)\left(\sqrt{m}-\dfrac{1}{3}\right)=0\)=>\(\left[{}\begin{matrix}\sqrt{m}-1=0\\\sqrt{m}-\dfrac{1}{3}=0\end{matrix}\right.< =>\left\{{}\begin{matrix}m=1\left(TM\right)\\m=\dfrac{1}{3}\left(loai\right)\end{matrix}\right.\)
vậy m=1 thì pt đã cho có 2 nghiệm (x,y) thỏa mãn
\(\sqrt{x}+\sqrt{y}=\sqrt{2}\)
Đúng 1
Bình luận (0)
chỗ cuối sửa thành x=1/9 (loại ) hộ :((
Đúng 1
Bình luận (0)