Cho hình thang ABCD (AB//CD) có AB = AD = 1/2 CD. Tính SABCD biết AB = 2,5cm và BD = 4cm
DD
Những câu hỏi liên quan
Cho hình thang ABCD
(
A
B
/
/
C
D
)
c
ó
A
B
A
D
C
D
/
2
.
Gọi M là trung điểm của CD và H là giao điểm của AM và BD.a) Chứng minh tứ giác ABMD là hình thoib) Chứng minh BD ⊥ BCc) Chứng minh ΔAHD và ΔCBD đồng dạngd) Biết A...
Đọc tiếp
Cho hình thang ABCD ( A B / / C D ) c ó A B = A D = C D / 2 . Gọi M là trung điểm của CD và H là giao điểm của AM và BD.
a) Chứng minh tứ giác ABMD là hình thoi
b) Chứng minh BD ⊥ BC
c) Chứng minh ΔAHD và ΔCBD đồng dạng
d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD.

a) Ta có: AB = AD = CD/2 và M là trung điểm của CD (gt)
⇔ AB = DM và AB // DM
Do đó tứ giác ABMD là hình bình hành có AB = AD. Vậy ABMD là hình thoi.
b) M là trung điểm của CD nên BM là trung tuyến của ΔBDC mà MB = MD = MC. Do đó ΔBDC là tam giác vuông tại B hay DB ⊥ BC
c) ABMD là hình thoi (cmt) ⇔ ∠D1 = ∠D2
Do đó hai tam giác vuông AHD và CBD đồng dạng (g.g)
d) Ta có :
![]()
Xét tam giác vuông AHB, ta có :

Dễ thấy tứ giác ABCM là hình bình hành (AB // CM và AB = CM)
⇒ BC = AM = 3 (cm)
Ta có:
![]()
M là trung điểm của DC nên
SBMD = SBMC = SBCD/2 = 3 (cm2) (chung đường cao kẻ từ B và MD = MC)
Mặt khác ΔABD = ΔMDB (ABCD là hình thoi)
⇔ SABD = SBMD = 3 (cm2)
Vậy SABCD = SABD + SBMD + SBMC = 9 (cm2)
Đúng 1
Bình luận (0)
Cho hình thang ABCD (AB // CD) có AB = AD = CD/2. Gọi M là trung điểm của CD và H là giao điểm của AM và BD.
a) Chứng minh tứ giác ABMD là hình thoi
b) Chứng minh BD ⊥ BC
c) Chứng minh ΔAHD và ΔCBD đồng dạng
d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD.
a: Xét tứ giác ABMD có
AB//MD
AB=MD
Do đó: ABMD là hình bình hành
mà AB=AD
nên ABMD là hình thoi
b: Xét ΔBDC có
BM là đường trung tuyến
BM=DC/2
DO đó: ΔBDC vuông tại B
c: Xét ΔAHD vuông tại H và ΔCBD vuông tại B có
\(\widehat{ADH}=\widehat{CDB}\)
Do đó: ΔAHD\(\sim\)ΔCBD
Đúng 0
Bình luận (0)
Cho hình thang ABCD (AB // CD) có AB = AD = CD/2. Gọi M là trung điểm của CD và H là giao điểm của AM và BD. a) Chứng minh tứ giác ABMD là hình thoi b) Chứng minh BD ⊥ BC c) Chứng minh ΔAHD và ΔCBD đồng dạng d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD.
a ) Ta có : \(AB=AD=\frac{CD}{2}\) và M là trung điểm của CD (gt)
\(\Leftrightarrow AB=DM\) và AB // DM
Do đó tứ giác ABMD là hình bình hành có AB = AD. Vậy ABMD là hình thoi.
b) M là trung điểm của CD nên BM là trung tuyến của \(\Delta BDC\) mà MB = MD = MC.
Do đó \(\Delta BDC\) là tam giác vuông tại B hay \(DB\perp BC\)
c) ABMD là hình thoi (cmt) \(\Leftrightarrow\widehat{D}_1=\widehat{D}_2\)
Do đó hai tam giác vuông AHD và CBD đồng dạng (g.g)
d) Ta có :
\(HB=HD=\frac{1}{2}BD=\frac{1}{2}.4=2\left(cm\right)\)
Xét tam giác vuông AHB, ta có :
\(AH=\sqrt{AB^2-HB^2}\) ( định lí Pitago )
\(=\sqrt{2,5^2-2^2}=1,5\left(cm\right)\)
\(\Rightarrow AM=3\left(cm\right)\)
Dễ thấy tứ giác ABCM là hình bình hành (AB // CM và AB = CM)
\(\Rightarrow BC=AM=3\left(cm\right)\)
Ta có :
\(S_{BDC}=\frac{1}{2}BD.BC=\frac{1}{2}.4.3=6\left(cm^2\right)\)
M là trung điểm của DC nên
\(S_{BMD}=S_{BMC}=\frac{S_{BCD}}{2}=3\left(cm^2\right)\)
(chung đường cao kẻ từ B và MD = MC)
Mặt khác \(\Delta ABD=\Delta MDB\) ( ABCD là hình thoi )
\(\Leftrightarrow S_{ABD}=S_{BMD}=3\left(cm^2\right)\)
Vậy \(S_{ABCD}=S_{ABD}+S_{BMD}+S_{BMC}=9\left(cm^2\right)\)
Chúc bạn học tốt !!!
Đúng 0
Bình luận (0)
Cho hình thang ABCD (AB // CD) có AB = AD = CD/2. Gọi M là trung điểm của CD và H là giao điểm của AM và BD.
a) Chứng minh tứ giác ABMD là hình thoi
b) Chứng minh BD ⊥ BC
c) Chứng minh ΔAHD và ΔCBD đồng dạng
d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD
TL:
a)AB//DM
AB=DM(cùng bằng 1/2 CD)
=>ABMD là hbh
=>AD=BM
=>AB=BM=MD=DA=>ABMD là hình thoi
b)tam giác CBM cân tại M => góc C= góc CBM
tam giác MBD cân tại M => góc B= góc BDM
=>góc DBC = góc C + góc BDC = 90*
c)ABMD là hình thoi => AM vuông góc với BD => góc H = 90*
tam giác ADH và tam giác CDB có :
góc H = góc B =90*
góc ADB = BDM
=> tam giác ADH ~ tam giác CBD(g-g)
d)AB=2.5=>CD=5
Áp dụng định lí Pitago vào tam giác vuông BCD
ta tính đc BC = 3cm
Diên tích tam giác BDC = 3*4/2=6cm2
Diện tích tam giác ABD = 1.5 * 4/2 = 3cm2
=> Diện tích hình thang ABCD = 9cm2
~ t.i.c.k nha ~
Đúng 1
Bình luận (0)
Bạn tham khảo bài này nhé : https://h.vn/hoi-dap/question/619973.html
~Study well~
Đúng 0
Bình luận (0)
cho hình thang ABCD (AB//CD) có: AB=4cm;BD=6cm;CD=9cm.Gọi I là giao điểm của AC và BD hỏi:
Tính SABCD biết SABD= 16cm vuông
Bài 1: Cho hình thang vuông ABCD có góc A = góc D = 90o , AB = 4cm , CD = 9cm. Tính BD (biết BD vuông góc với BC)
Bài 2: Cho hình thang ABCD , AB//CD , BD là đường cao của hình thang, góc A + góc C = 90o , AB= 1cm, CD= 3cm. Tính AD và BC
Bài 3: Cho hình chữ nhật ABCD, AB= 4cm, AD= 3cm. Gọi E và F là hình chiếu của A và C trên BD. Tính EF
Bài 1: Cho hình thang vuông ABCD có góc A = góc D = 90o , AB = 4cm , CD = 9cm. Tính BD (biết BD vuông góc với BC)
Bài 2: Cho hình thang ABCD , AB//CD , BD là đường cao của hình thang, góc A + góc C = 90o , AB= 1cm, CD= 3cm. Tính AD và BC
Bài 3: Cho hình chữ nhật ABCD, AB= 4cm, AD= 3cm. Gọi E và F là hình chiếu của A và C trên BD. Tính EF
Bài 1: Cho hình thang vuông ABCD có góc A = góc D = 90o , AB = 4cm , CD = 9cm. Tính BD (biết BD vuông góc với BC)
Bài 2: Cho hình thang ABCD , AB//CD , BD là đường cao của hình thang, góc A + góc C = 90o , AB= 1cm, CD= 3cm. Tính AD và BC
Bài 3: Cho hình chữ nhật ABCD, AB= 4cm, AD= 3cm. Gọi E và F là hình chiếu của A và C trên BD. Tính EF
Hình thang ABCD (AB // CD) có AB =2,5cm, AD = 3,5cm, BD=5cm và ∠ (DAB) = ∠ (DBC). Tính độ dài BC, CD.
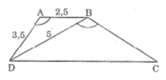
Vì
△
ABD ∼
△
BDC nên: 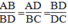
Với AB = 2,5cm; AD = 3,5cm; BD = 5cm, ta có:
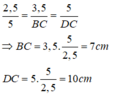
Đúng 0
Bình luận (0)


