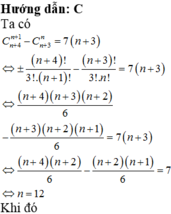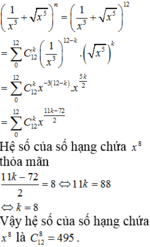Tìm dạng tổng quát của số nguyên dương a,b biết M=n.4n+3n\(⋮\)7
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
HT
Những câu hỏi liên quan
Tìm dạng tổng quát của số nguyên dương a,b biết: \(M=n.4^n+3^n⋮7\)
Nếu n có dạng 2k ( k nguyên dương )
Khi đó:
\(M=2k\cdot4^{2k}+3^{2k}=2k\cdot16^k+9^k\)
Ta có:
\(16^k\equiv2^k\left(mod7\right);9^k\equiv2^k\left(mod7\right)\Rightarrow2k\cdot2^k+2^k\equiv M\left(mod7\right)\)
\(\Rightarrow M\equiv2^k\left(2k+1\right)\left(mod7\right)\Rightarrow2k+1⋮7\Rightarrow k\) chia 7 dư 3
\(\Rightarrow k\) có dạng 7q+3
Khi đó n có dạng 14q+6
Nếu n có dạng 2k+1 ( k là số nguyên dương )
Khi đó:
\(M=n\cdot4^n+3^n=\left(2k+1\right)\cdot4^{2k+1}+3^{2k+1}=4\left(2k+1\right)\cdot16^k+3\cdot9^k\)
Tương tự ta có:
\(M\equiv\left(8k+4\right)\cdot2^k+3\cdot2^k\left(mod7\right)\Rightarrow M\equiv2^k\left(8k+7\right)\left(mod7\right)\)
\(\Rightarrow8k+7⋮7\Rightarrow8k⋮7\Rightarrow k⋮7\Rightarrow k\) có dạng 7p
Khi đó:\(n=2k+1=14p+1\)
Vậy......
Tìm hệ số của số hạng chứa
x
8
trong khai triển nhị thức Newton của
1
x
3
+
x
5
n
, biết rằng
C
n
+
4...
Đọc tiếp
Tìm hệ số của số hạng chứa x 8 trong khai triển nhị thức Newton của 1 x 3 + x 5 n , biết rằng C n + 4 n + 1 - C n + 3 n = 7 ( n + 3 ) . (với n là số nguyên dương và x > 0)
A. 400
B. 480
C. 495
D. 0
Tìm một số nguyên âm có dạng tổng quát là -abc biết a là số dư của phép chia 8:5, b là số liền sau của số đó và c là số không phảo số nguyên âm cũng không phải số nguyên dương
8 : 5 dư 3 => a = 3
số liền sau của 3 là 4 => b = 4
số không phải số nguyên âm không phải số nguyên dương là số 0 => c = 0
vậy số cần tìm là -340
Đúng 0
Bình luận (0)
Tìm n là số nguyên dương biết 5^3n.5^3n+5.5^4n < hoặc=10^16:2^16
Tìm n thuộc Z , Biết :
a, -18/n là số nguyên
b, n+7/ 3n -1 là số nguyên
c, 3n+2/4n-5 là số tự nhiên
a/
Với $n$ nguyên, để $\frac{-18}{n}$ là số nguyên thì $n$ là ước của $-18$
$\Rightarrow n\in \left\{\pm 1; \pm 2; \pm 3; \pm 6; \pm 9; \pm 18\right\}$
b.
Với $n$ nguyên, để $\frac{n+7}{3n-1}$ nguyên thì:
$n+7\vdots 3n-1$
$\Rightarrow 3(n+7)\vdots 3n-1$
$\Rightarrow (3n-1)+22\vdots 3n-1$
$\Rightarrow 22\vdots 3n-1$
$\Rightarrow 3n-1\in\left\{\pm 1; \pm 2; \pm 11; \pm 22\right\}$
$\Rightarrow n\in \left\{\frac{2}{3}; 0; 1; \frac{-1}{3}; 4; \frac{-10}{3}; \frac{23}{3}; -7\right\}$
Do $n$ nguyên nên $n\in\left\{0; 1; 4; -7\right\}$
Đúng 0
Bình luận (0)
a/
Với $n$ nguyên, để $\frac{-18}{n}$ là số nguyên thì $n$ là ước của $-18$
$\Rightarrow n\in \left\{\pm 1; \pm 2; \pm 3; \pm 6; \pm 9; \pm 18\right\}$
b.
Với $n$ nguyên, để $\frac{n+7}{3n-1}$ nguyên thì:
$n+7\vdots 3n-1$
$\Rightarrow 3(n+7)\vdots 3n-1$
$\Rightarrow (3n-1)+22\vdots 3n-1$
$\Rightarrow 22\vdots 3n-1$
$\Rightarrow 3n-1\in\left\{\pm 1; \pm 2; \pm 11; \pm 22\right\}$
$\Rightarrow n\in \left\{\frac{2}{3}; 0; 1; \frac{-1}{3}; 4; \frac{-10}{3}; \frac{23}{3}; -7\right\}$
Do $n$ nguyên nên $n\in\left\{0; 1; 4; -7\right\}$
Đúng 0
Bình luận (0)
c/ Với $n$ nguyên, để $\frac{3n+2}{4n-5}$ là số tự nhiên thì:
$3n+2\vdots 4n-5$
$\Rightarrow 4(3n+2)\vdots 4n-5$
$\Rightarrow 3(4n-5)+23\vdots 4n-5$
$\Rightarrow 23\vdots 4n-5$
$\Rightarrow 4n-5\in \left\{\pm 1; \pm 23\right\}$
$\Rightarrow n\in \left\{\frac{3}{2}; 1; 7; \frac{-9}{2}\right\}$
Do $n$ nguyên nên $n=1$ hoặc $n=7$
Thử lại thấy $n=7$ là kết quả duy nhất thỏa mãn phân số đã cho là số tự nhiên.
Đúng 0
Bình luận (0)
Tìm số nguyên n sao cho:
a) (n+1)/(n-2) là số nguyên âm.
b) (n+7)/(3n-1) là số nguyên.
c) (3n+2)/(4n-5) là số tự nhiên.
Cho dãy số
u
n
được xác định bởi
u
1
2
;
u
n
2
u
n
-
1
+
3
n
-
1
.
Công thức số hạng tổng quát của dãy số đã cho là biểu thức có dạng
a
.
2...
Đọc tiếp
Cho dãy số u n được xác định bởi u 1 = 2 ; u n = 2 u n - 1 + 3 n - 1 . Công thức số hạng tổng quát của dãy số đã cho là biểu thức có dạng a . 2 n b n + c , với a, b, c là các số nguyên, n ≥ 2 , n ∈ N . Khi đó, tổng a + b + c có giá trị bằng ?
A. -4
B. 4
C. -3
D. 3
3. tìm số nguyên n sao cho
a) n+3/ n -2 là số nguyên
b) n+7/ 3n -1 là số nguyên
c)3n+2/ 4n-5 là số nguyên
a)Để n+3/n-2 thuộc Z
=>n+3 chia hết n-2
=>n-2+5 chia hết n-2
=>5 chia hết n-2
=>n-2 thuộc Ư(5)={1;-1;5;-5}
=>n thuộc {3;1;7;-3}
Đúng 1
Bình luận (0)
a)Để \(\frac{\text{n+3}}{\text{n-2}}\) \(\in\) Z
=> n+3 chia hết n-2
=> (n-2) +5 chia hết n-2
=>5 chia hết n-2
=>n-2 thuộc Ư(5)={1;-1;5;-5}
Ta có:
| n -2 | 1 | -1 | -5 | 5 |
| n | 3 | 1 | -3 | 7 |
Đúng 1
Bình luận (0)
Tính giới hạn của các dãy số có số hạng tổng quát sau đây, khi n → + ∞
u
n
3
n
-
4
n
+
1
2
.
4...
Đọc tiếp
Tính giới hạn của các dãy số có số hạng tổng quát sau đây, khi n → + ∞ u n = 3 n - 4 n + 1 2 . 4 n + 2 n
l i m u n = l i m 3 n - 4 n + 1 2 . 4 n + 2 n = - 1 2
Đúng 0
Bình luận (0)