cho dãy số A= 5+52+53+....+52013
a) Thu gọn A
b) 4A+5=5x . tìm x
Cho A = 5 + 52 + 53 + … + 52022. Tìm x để 4A + 5 = 5x
Cho Tìm số tự nhiên biết .
A= 1 + 5 + 52 + 5 3 + ... + 5800
5A= 5 + 52 + 53 + .... +5 800 + 5801
5A - A = 5801 - 1
4a = 5801 - 1
5801 - 1 +1 = 5n
⇒ 5801 = 5n ⇒ n = 801
bài 1 tìm x biết
a:34+3x=130
b 54-4(5+x)=10
c 42022 . (5x-4) =42024
2 .(x+1)3= 54
bài 2 cho A= 5+52+53+...+52022.tìm x để 4A+5=5x
bài 3 cho A=4+42+43+...+42023+42024
a tính giá trị của biểu thức A
b biểu thức A có chia hết cho 20 ko?vì sao?
bài 4 cho biểu thức A=2+22+23+...+2100
a A có chia hết cho 6 ko ? vì sao?
b A có chia hết cho 7 ko ? vì sao?
giúp mình với mình đang cần gấp
bài 1 có ý d nha các bạn mình viết thiếu
Bài dái quá, bạn nên tách ra đi nhé!
bài 6 :
1) cho p và p + 8 đều là số nguyên tố (p>3). hỏi p + 100 là số nguyên tố hay hợp số ?
2) trog một phép chia,số bị chia bằng 63,số dư bằng 8. tìm số chia và thương
3) cho A = 5 +52 + 53 +...+52016. Tìm x để 4A + 5 = 5x.
4) chúng minh rằng tích của 4 số tự nhiên liên tiếp cộng 1 luôn là số chính phương.
5) chứng tỏ rằng tổng A = 405n + 2405 + m2
6) Cho S = 1 + 3 + 32 + 33 + ...+ 398. Chứng minh S không phải là số chính phương.
7) So sánh hai hiệu : 20182019 - 20182018 và 20182018 - 20182017.
8) Khi chia một số cho 255 ta được số dư là 100. hỏi số đó chia hết cho 85 không? Vì sao? Nếu có dư thì số như là bao nhiêu?
9) Chứng minh rằng với mọi số tự nhiên n thì n2 + n +1 không chia hết cho 4.
mình chia 2 phần ạ. còn phần 2 mình sẽ viết. mong mn giúp mình ạ ^^ mình cần rất gấp vì mai mình đi học rồi. mn ko giúp mình là coi như mình toang luôn T-T
Bài 4: Tìm x là số tự nhiên biết:
Cho B =5 + 52 + 53 + ........ + 52022
a) Tính B
b) Tìm x để 4B + 5 = 5x
Nhanh giúp mình ạ
a) \(B=5+5^2+5^3+...+5^{2022}\)
\(\Rightarrow5B=5^2+5^3+5^4+...+5^{2023}\)
\(\Rightarrow4B=5^{2023}-5\)
b) \(4B+5=5^X\)
Hay \(5^{2023}-5+5=5^X\)
\(5^{2023}=5^x\)
\(\Rightarrow x=2023\)
B = 5 + 52 + 53 +...+ 52022
5.B = 52 + 53 +....+ 52023
5B- B = 52023 - 5
4B = 52023 - 5
b, 4B + 5 = 5\(^x\) ⇒ 52023 - 5 + 5 = 5\(^x\)
5\(^{2023}\) = 5\(x\)
\(x\) = 2023
Nguyễn Thị Thương Hoài
Cô ơi, x = 2023 vì x nằm ở mũ nha cô.
1)Tìm số dư của phép chia B cho 4
B=1+3+32+33+...+3100
2)Thu gọn C=5-52+53-54+...+52023-52024
Bài 1:
$B=1+3+3^2+3^3+...+3^{100}$
$=1+(3+3^2)+(3^3+3^4)+...+(3^{99}+3^{100})$
$=1+3(1+3)+3^3(1+3)+...+3^{99}(1+3)$
$=1+(1+3)(3+3^3+...+3^{99})=1+4(3+3^3+....+3^{99})$
$\Rightarrow B$ chia 4 dư 1.
Bài 2:
$C=5-5^2+5^3-5^4+...+5^{2023}-5^{2024}$
$5C=5^2-5^3+5^4-5^5+...+5^{2024}-5^{2025}$
$\Rightarrow C+5C=5-5^{2025}$
$6C=5-5^{2025}$
$C=\frac{5-5^{2025}}{6}$
Bài 1: Tìm x là số tự nhiên, biết:
1. Cho A = 21 + 22 + 23 + ....... + 22022
2. Cho B = 5 + 52 + 53 +...........+ 52022
a) Tính A,B
b) Tìm x để A + 2 = 2x
Tìm x để biết 4B + 5 = 5x
Nhanh giúp mình với ạ!
a) Ta có A = 21 + 22 + 23 + ... + 22022
2A = 22 + 23 + 24 + ... + 22023
2A - A = ( 22 + 23 + 24 + ... + 22023 ) - ( 21 + 22 + 23 + ... + 22022 )
A = 22023 - 2
Lại có B = 5 + 52 + 53 + ... + 52022
5B = 52 + 53 + 54 + ... + 52023
5B - B = ( 52 + 53 + 54 + ... + 52023 ) - ( 5 + 52 + 53 + ... + 52022 )
4B = 52023 - 5
B = \(\dfrac{5^{2023}-5}{4}\)
b) Ta có : A + 2 = 2x
⇒ 22023 - 2 + 2 = 2x
⇒ 22023 = 2x
Vậy x = 2023
Lại có : 4B + 5 = 5x
⇒ 4 . \(\dfrac{5^{2023}-5}{4}\) + 5 = 5x
⇒ 52023 - 5 + 5 = 5x
⇒ 52023 = 5x
Vậy x = 2023
Bài 3 (1điểm): Cho A = 5 + 52 + 53 + … + 5992 Chứng minh rằng: 4A + 5 là một luỹ thừa của 125.
\(A=5+5^2+5^3+...+5^{992}\)
\(\Rightarrow5A=5^2+5^3+5^4+...+5^{993}\)
\(\Rightarrow4A=5A-A=5^2+5^3+5^4+...+5^{993}-5-5^2-5^3-...-5^{992}=5^{993}-5\)
\(\Rightarrow4A+5=5^{993}-5+5=5^{993}=\left(5^3\right)^{331}=125^{331}\) là một lũy thừa của 125
bài 6:
a) Tìm cặp số x,y nguyên biết: (x - 3).(y+1)=5
b) Cho A = 21 + 5 + 52 + 53 + ... + 599.Tìm số dư của phép chia khi lấy A chia cho 6
Lời giải:
a. $(x-3)(y+1)=5=1.5=5.1=(-1)(-5)=(-5)(-1)$
Vì $x-3, y+1$ cũng là số nguyên nên ta có bảng sau:
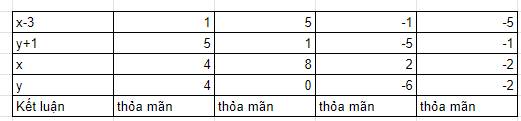
b.
$A=21+5+(5^2+5^3)+(5^4+5^5)+....+(5^{98}+5^{99})$
$=26+5^2(1+5)+5^4(1+5)+....+5^{98}(1+5)$
$=2+24+(1+5)(5^2+5^4+...+5^{98}$
$=2+24+6(5^2+5^4+....+5^{98})=2+6(4+5^2+5^4+...+5^{98})$
$\Rightarrow A$ chia $6$ dư $2$.