Chứng minh rằng :
(a+1)(b+1)(a+c)(b+c)≥16abc
với a,b,c là những số dương tùy ý
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
LL
Những câu hỏi liên quan
Chứng minh rằng:
(a + 1)(b + 1)(a + c)(b + c) ≥ 16abc, với a, b, c là những số dương tùy ý.
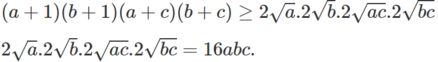
⇒(a + 1)(b + 1)(a + c)(b + c) ≥ 16abc.
Đúng 0
Bình luận (0)
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
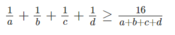
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
Chứng minh rằng :
\(a+b+c\le\dfrac{1}{2}\left(a^2b+b^2c+c^2a+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\)
với a, b, c là những số dương tùy ý
Áp dụng bất đẳng thức Cauchy - Schwarz
\(\Rightarrow\left\{{}\begin{matrix}a^2b+\dfrac{1}{b}\ge2\sqrt{\dfrac{a^2b}{b}}=2a\\b^2c+\dfrac{1}{c}\ge2\sqrt{\dfrac{b^2c}{c}}=2b\\c^2a+\dfrac{1}{a}\ge2\sqrt{\dfrac{c^2a}{a}}=2c\end{matrix}\right.\)
\(\Rightarrow a^2b+b^2c+c^2a+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge2\left(a+b+c\right)\)
\(\Rightarrow\dfrac{1}{2}\left(a^2b+b^2c+c^2a+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge a+b+c\) ( đpcm )
Dấu " = " xảy ra khi \(a=b=c=1\)
Đúng 0
Bình luận (0)