Cho hàm số y=mx(m#0)
a)Xác định m để đồ thị của hàm số đi qua điểm A(-1;1)
b)Vẽ đồ thị của hàm số ứng với m vừa tìm được
c)Hãy xác định m để đồ thị của hàm số y=mx nằm trong góc phần tư thứ I và III
HN
Những câu hỏi liên quan
1. cho hàm số y=(m-1)x+m
a) tìm m để đồ thị hàm số cắt đồ thị y=mx+3
b) tìm m để dồ thị hàm số vuông góc với đồ thị y=-mx+1
Cho hàm số : y = mx + m + 6
CMR: khi m thay đổi thì hàm số y = mx + m + 6 luôn đi qua 1 điểm cố định
Điều kiện cần và đủ để hàm số đi qua điểm cố định \(M\left(x_0;y_0\right)\) là:
\(y_0=mx_0+m+6\left(\forall m\right)\)
\(\Leftrightarrow m\left(x_0+1\right)+y_0-6=0\left(\forall m\right)\)
\(\Leftrightarrow\hept{\begin{cases}x_0+1=0\\y_0-6=0\end{cases}\Leftrightarrow\hept{\begin{cases}x_0=-1\\y_0=6\end{cases}}}\)
Vậy hàm số y = mx + m - 6 luôn đi qua điểm cố định \(M\left(-1;6\right)\) với mọi m
). Cho hàm số y mx + 3. a. Tìm m, biết rằng khi x 1 thì y 1. Vẽ đồ thị của hàm số với giá trị m tìm được.b. Viết phương trình đường thẳng (d) đi qua điểm M(0; -3) và song song với đường thẳng y -2x + 3.). Cho hàm số y mx + 3. a. Tìm m, biết rằng khi x 1 thì y 1. Vẽ đồ thị của hàm số với giá trị m tìm được.b. Viết phương trình đường thẳng (d) đi qua điểm M(0; -3) và song song với đường thẳng y -2x + 3.). Cho hàm số y mx + 3. a. Tìm m, biết rằng khi x 1 thì y 1. Vẽ đồ thị của hàm số...
Đọc tiếp
). Cho hàm số y = mx + 3.
a. Tìm m, biết rằng khi x = 1 thì y = 1. Vẽ đồ thị của hàm số với giá trị m tìm được.
b. Viết phương trình đường thẳng (d) đi qua điểm M(0; -3) và song song với đường thẳng y = -2x + 3.
). Cho hàm số y = mx + 3.
a. Tìm m, biết rằng khi x = 1 thì y = 1. Vẽ đồ thị của hàm số với giá trị m tìm được.
b. Viết phương trình đường thẳng (d) đi qua điểm M(0; -3) và song song với đường thẳng y = -2x + 3.). Cho hàm số y = mx + 3.
a. Tìm m, biết rằng khi x = 1 thì y = 1. Vẽ đồ thị của hàm số với giá trị m tìm được.
b. Viết phương trình đường thẳng (d) đi qua điểm M(0; -3) và song song với đường thẳng y = -2x + 3.
). Cho hàm số y = mx + 3.
a. Tìm m, biết rằng khi x = 1 thì y = 1. Vẽ đồ thị của hàm số với giá trị m tìm được.
b. Viết phương trình đường thẳng (d) đi qua điểm M(0; -3) và song song với đường thẳng y = -2x + 3.
a: Thay x=1 và y=1 vào (d), ta được:
m+3=1
hay m=-2
b: Vì (d)//y=-2x+3 nên a=-2
Vậy: (d): y=-2x+b
Thay x=0 và y=-3 vào (d), ta được:
b=-3
Đúng 1
Bình luận (1)
Cho hàm số y=mx-3
A, vẽ đồ thị hàm số khi m=1
B, tìm hàm số m . biết đồ thị đi qua M(3;6)
Lời giải:
a. Khi $m=1$ thì hàm số là: $y=x-3$
ĐTHS được minh họa dưới đây:
b. Để đths đi qua $M(3;6)$ thì:
$y_M=mx_M-3$
$\Leftrightarrow 6=3m-3$
$\Leftrightarrow 9=3m$
$\Leftrightarrow m=3$
Đúng 1
Bình luận (0)
Cho hàm số y=MX+1
Tìm m để đồ thì hàm số song song vs đường thẳng y=(m²-2)+2+3
Xem chi tiết
Cho hàm số y = 2x + 2
a. Vẽ đồ thị của hàm số đã cho .
b. Tìm m để đồ thị hàm số y = mx + m + 1 cắt đồ thị hàm số đã cho tại điểm nằm trên trục tung .
b: Để hai đường cắt nhau trên trục tung thì
m<>2 và m+1=2
=>m=1
a: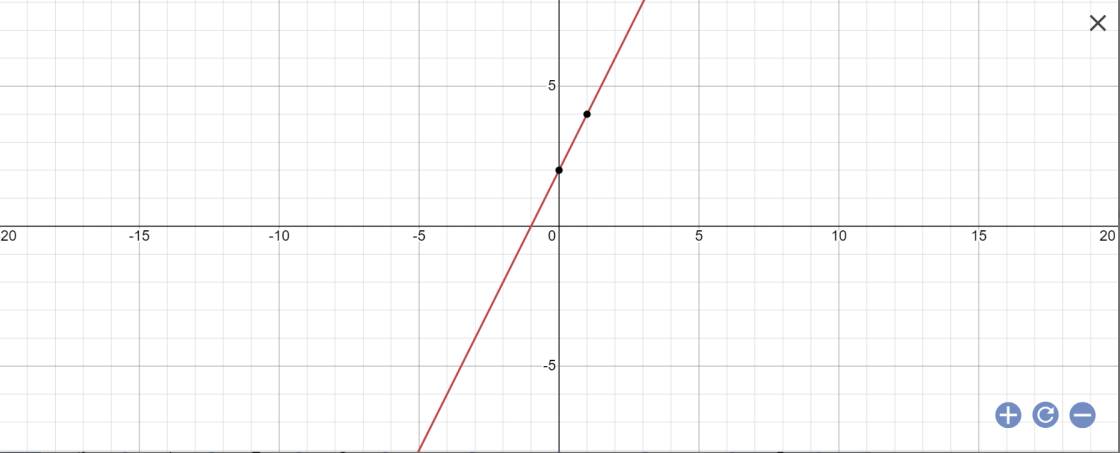 
Đúng 0
Bình luận (0)
Cho hàm số y
m
x
+
4
x
+
m
. Giá trị của m để hàm số đồng biến trên
(
2
;
+
∞
)
là? A. m 2 B. m -2 hoặc m 2 C. m
≤
-2 D. m -2
Đọc tiếp
Cho hàm số y = m x + 4 x + m . Giá trị của m để hàm số đồng biến trên ( 2 ; + ∞ ) là?
A. m > 2
B. m < -2 hoặc m > 2
C. m ≤ -2
D. m < -2
Chọn A.
Điều kiện xác định của hàm số x ≠ -m
Đạo hàm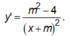 
Hàm số đã cho đồng biến trên ( 2 ; + ∞ ) khi và chỉ khi
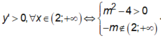
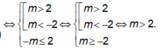
Vậy khi m > 2 thì hàm số đã cho đồng biến trên ( 2 ; + ∞ )
Đúng 0
Bình luận (0)
Cho hàm số
y
m
x
+
4
x
+
m
.
Giá trị của m để hàm số đồng biến trên
2
;
+
∞
là? A.m2 B....
Đọc tiếp
Cho hàm số y = m x + 4 x + m . Giá trị của m để hàm số đồng biến trên 2 ; + ∞ là?
A.m>2
B. m < - 2 m > 2 .
C. m ≤ - 2 .
D.m<-2
Cho hàm số
y
x
3
3
-
m
+
1
x
2
+
m
x
-
2
. Tìm m để hàm số đạt cực đại tại x -1 A. m -1 B. m 1 C. không có m D. m -2
Đọc tiếp
Cho hàm số y = x 3 3 - m + 1 x 2 + m x - 2 . Tìm m để hàm số đạt cực đại tại x = -1
A. m = -1
B. m = 1
C. không có m
D. m = -2
Cho hàm số y = mx + m - 2x
a) Tìm m để y là hàm số bậc nhất
b) Tìm m để y là hàm số nghịch biến
c) Tìm m để y là hàm số đồng biến
a) Ta có \(y=mx+m-2x=\left(m-2\right)x+m\)
Như vậy để y là hàm số bậc nhất thì \(m-2\ne0\Leftrightarrow m\ne2\)
b) Để y là hàm số nghịch biến thì \(m-2< 0\Leftrightarrow m< 2\)
c) Để y là hàm số đồng biến thì \(m-2>0\Leftrightarrow m>2\)