Bài tập 8 skg trang 63 toán đại số 10
3x2 - 2(m+1)x + 3m-5=0
Giúp em giải với ạ
Giả sử 
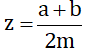
Giả sử 
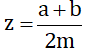
Cái bài này mình đã từng đăng để hỏi mấy bạn kia.
Nhưng đề câu này thiểu bạn ơi.
Phải có x=a/m ; y=b/m
À thôi, mk viết đầy đủ đề thử nhé !
Giả sử:x=a/m;y=b/m (a,b,m thuộc Z.m > 0) và x < y.
Hãy chứng minh (chứng tỏ) rằng nếu chọn z=a+b/2m thì ta có x < y < z.
Trong sách lớp 7 đề y như z đó !
Mk ghi cách làm luôn nha !
Giả sử x=a/m,y=b/m (a,b,m thuộc Z,m > 0 )
Vì x < y nên ta suy ra a < b.
ta có: x=a/m, y=b/m <=> x=2a/am. y=2b/2m
mà a < b nên a+a < a+b <=> 2a < a+b
Do 2a < a+b thì x < y ( 1 )
Ta lại có: a < b nên a+b < b+b <=> a+b < 2b
Mà a+b < 2b <=> x < z ( 2 )
Từ ( 1 ) và ( 2 ) suy ra x < y < z (ĐPCM)
Tóm tắt lý thuyết và Giải bài 90,91,92, 93,94,95, 96, 97 trang 95; Bài 98, 99,100 trang 96 SGK Toán 6 tập 1: Tính chất của phép nhân.
A. Tóm tắt lý thuyết tính chất của phép nhân
Tính chất giao hoán: a.b = b.aTính chất kết hợp: (a.b).c = a.(b.c)Nhân với số 1: a.1 = 1.a = aTính chất phân phối của phép nhân đối với phép cộng:a.(b + c) = a.b + a.c.
Lưu ý: Ta cũng có: a.(b – c) = a.b – a.c
Bài trước: Nhân hai số nguyên cùng dấu
B. Đáp án và hướng dẫn giải bài tập SGK bài tính chất của phép nhân trang 95,96 Toán 6 – Chương 2 số học.
Bài 90 trang 95 SGK Toán 6 tập 1 – Số học
Thực hiện các phép tính:
a) 15.(-2).(-5).(-6); b) 4.7.(-11).(-2).
Đáp án và giải bài 90:
a) 15.(-2).(-5).(-6) = [15.(-6)].[(-2).(-5)] = (-90).10 = -900
b) 4.7.(-11).(-2) = (4.7).[(-2).(-11)] = 28.22 = 616
Bài 91 trang 95 SGK Toán 6 tập 1 – Số học
Thay một thừa số bằng tổng để tính:
a) -57.11; b) 75.(-21).
Đáp án và giải bài 91:
Hướng dẫn: Thay 11 bởi 10 + 1; thay -21 bởi -20 – 1.
a) -57.11= -57.(10+1) = -570 -57 = -627;
b)75.(-21)= 75.(-20-1)= -1500 – 75 = -1575
Bài 92 trang 95 SGK Toán 6 tập 1 – Số học
Tính:
a) (37 – 17).(-5) + 23.(-13 – 17);
b) (-57).(67 – 34) – 67.(34 – 57).
Bài giải:
a) (37 – 17).(-5) + 23.(-13 – 17) = 20.(-5) + 23.(-30)
= -100 – 690 = -790.
b) Cách 1:
(-57).(67 – 34) – 67.(34 – 57)= (-57).67 – (-57).34 – 67.34 + 67.57
= 67.(-57 + 57) – [34.(-57) + 34.67] = 0 – 34.(-57 + 67) = -34.10. = -340.
Cách 2:
(-57).(67 – 34) – 67.(34 – 57) = (-57).33 – 67.(-23) = -1881 + 1541 = -340.
Bài 93 trang 95 SGK Toán 6 tập 1 – Số học
Tính nhanh:
a) (-4).(+125).(-25).(-6).(-8);
b) (-98).(1 – 246) – 246.98.
Đáp án và hướng dẫn giải bài 93:
a) Hoán vị để có: [(-4).(-25)].[125.(-8)].(-6).
b) Áp dụng tính chất phân phối.
a) (4).(+125).(-25).(-6).(-8) = [(-4).(-25)].[125.(-8)].(-6) =100.(-1000).(-6) = 600000
b) (-98)(1-246)-246.98 = -98 + 246.98 – 246.98 = -98
Bài 94 trang 95 SGK Toán 6 tập 1 – Số học
Viết các tích sau dưới dạng một lũy thừa:
a) (-5) . (-5) . (-5) . (-5) . (-5);
b) (-2) . (-2) . (-2) . (-3) . (-3) . (-3).
Đáp án bài 94:
ĐS: a) (-5)5; b) 63.
Bài 95 trang 95 SGK Toán 6 tập 1 – Số học
Giải thích vì sao: (-1)3 = -1. Có còn số nguyên nào khác mà lập phương của nó bằng chính nó ?
Đáp án bài 95:
(-1)3 = (-1) . (-1) . (-1) = 1 . (-1) = -1.
Còn còn số nguyên 1,0 mà lập phương của nó bằng chính nó. (1)3 = 1 và số (0)3 = 0.
Bài 96 trang 95 SGK Toán 6 tập 1 – Số học
Tính:
a) 237.(-26) + 26.137; b) 63.(-25) + 25.(-23).
Đáp án và giải bài 96:
a) 237.(-26) + 26.137 = -237.26 + 26.137 = 26.(-237 + 137)
= 26.(-100) = -2600.
b) Cách 1: 63.(-25) + 25.(-23) = -63.25 + 25.(-23) = 25.(-63 – 23)
= 25.(-86) = -2150.
Cách 2: 63.(-25) + 25.(-23) = -1575 – 575 = -2150.
Bài 97 trang 95 SGK Toán 6 tập 1 – Số học
So sánh:
a) (-16).1253.(-8).(-4).(-3) với 0;
b) 13.(-24).(-15).(-8).4 với 0.
Đáp án và giải bài 97:
a) (-16).1253.(-8).(-4).(-3) > 0.
Tích này lớn hơn 0 vì trong tích có 4 thừa số âm Tích dương.
b) 13.(-24).(-15).(-8).4 < 0
Tích này nhỏ hơn 0 vì trong tích có 3 thừa số âm tích âm.
Bài 98 trang 96 SGK Toán 6 tập 1 – Số học
Tính giá trị của biểu thức:
a) (-125).(-13).(-a), với a = 8.
b) (-1).(-2).(-3).(-4).(-5).b, với b = 20.
Đáp án và giải bài 98:
a, (-125).(-13).(-a) = (-125).(-13).(-8)
= [(-125). (-8)] .(-13) = -13000
b, (-1).(-2).(-3).(-4).(-5).b = (-1).(-2).(-3).(-4).(-5). 20 = (-120).20 = -2400
Bài 99 trang 96 SGK Toán 6 tập 1 – Số học
Áp dụng tính chất a(b – c) = ab – ac, điền số thích hợp vào ô trống:
a)[ ].(-13) + 8.(-13) = (-7 + 8).(-13) = [ ]
b) (-5).(-4 – [ ]) = (-5).(-4) – (-5).(-14) = [ ]
Đáp án và giải bài 99:
a) (-7).(-13) + 8.(-13) = (-7 + 8).(-13) = -13
b) (-5).[-4 – (-14)] = (-5).(-4) – (-5).(-14) = -50.
Bài 100 trang 96 SGK Toán 6 tập 1 – Số học
Giá trị của tích m.n2 với m = 2, n = -3 là số nào trong bốn đáp số A, B, C, D dưới đây:
A. -18; B. 18; C. -36; D. 36.
Đáp án và hướng dẫn giải bài 100:
Với m =2; n = -3
Ta có m.n2 =2.(-3)2 = 2.9 =18
Vậy chọn B: 18
bài toán đại số bài 63 trang 34 tập 2
ghi đề bài rõ ra nha bạn
HT
Dạng 4 : Phân thức đại số các phép toán trên phân thức . Bài tập 1 Thực hiện phép tính a,. 2/2x + 3x-3/2x-1 + 2x^2+1/4x^2-2x b, 5/6x^2y +7/12xy^2 + 11/18xy c,. x^3+2x/x^3+1 + 2x/x^2-x+1 + 1/x+1 Mn giúp em với ạ. Hãy cho em xin lời giải chi tiết từng bước làm ạ
c: \(=\dfrac{x^3+2x+2x^2+2x+x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{x^3+3x^2+3x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{x^2+2x+1}{x^2-x+1}\)
Bài 18 trang 7 SBT Toán 8 Tập 1: Chứng tỏ rằng:
a. x2 – 6x + 10 > 0 với mọi x
b. 4x – x2 – 5 < 0 với mọi x
a) \(x^2-6x+10=\left(x^2-6x+9\right)+1=\left(x-3\right)^2+1\ge1>0\forall x\)
b) \(4x-x^2-5=-\left(x^2-4x+4\right)-1=-\left(x-2\right)^2-1\le-1< 0\forall x\)
: Giải phương trình rồi kiểm nghiệm hệ vi-ét:
a. 5x2 + 2x -16 =0 b.3x2 -2x -5 =0
Phương trình 5x2 + 2x -16 =0 có hệ số a=5 ,b=2 c=-16
Ta có: Δ'=12 -5(-16) = 1 + 80 =81 >0
Δ' = 81 =9
Phương trình 3x2 -2x -5 =0 có hệ số a =3,b = -2, c = -5
Ta có: Δ'=(-1)2 -3(-5) = 1 + 15 =16 >0
Δ' = 16 =4
Phương trình 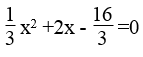
Δ'=32 -1(-16) = 9 +16 =25 > 0
Δ' = 25 =5
Phương trình 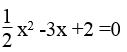
Ta có: Δ'=(-3)2 -1.4 = 9 -4 =5 >0
Δ' = 5
Giúp mình giải câu b và câu c bài 19 trang 7 sách bài tập toán 8:
b) Q = 2x^2 - 6x
c) M = x^2 + y^2 - x + 6y + 10
b) Q = 2x2 - 6x => 2Q = 4x2 - 12x => 2Q = (2x)2 - 2 . 2 . 3x + 9 - 9 => 2Q = (2x - 3)2 - 9 \(\ge\)-9 <=> Q \(\ge\)-4,5
Đẳng thức xày ra khi: (2x - 3)2 = 0 => x = 1,5
Vậy giá trị nhỏ nhất của Q là -4,5 khi x = 1,5
c) M = x2 + y2 - x + 6y + 10 => M = x2 + y2 - x + 6y + 0,25 + 9 + 0,75
=> M = (x2 - x + 0,25) + (y2 + 6y + 9) + 0,75
=> M = (x - 0,5)2 + (y + 3)2 + 0,75\(\ge\)0,75
Đẳng thức xảy ra khi: (x - 0,5)2 = 0 và (y + 3)2 = 0 <=> x = 0,5 và y = -3
Vậy giá trị nhỏ nhất của M là 0,75 khi x = 0,5 và y = -3
Cho phương trình: x2 – mx + m – 1 = 0 (1). Tìm m để phương trình (1) có hai nghiệm phân biệt x1 và x2 thoả mãn: x12 + 3x1x2 = 3x2 + 3m + 16.
giải giúp mình bài này với ạ, mình cảm ơn