Cho \(\Delta\)ABC có \(\widehat{A}\)= \(90^o\) và AB=AC. Tính số đo các góc B và C.
MA
Những câu hỏi liên quan
Cho Delta ABCcówidehat{ABC}55^o, trên cạnh AC lấy điểm D (D ko trùng với A và C)a. Tính độ dài AC, biết AD4cm, CD3cm.b. Tính số đo củawidehat{DBC}, biết widehat{ABD}30^o.c. Từ B dựng tia Bx sao cho widehat{DBx}90^o. Tính số đo widehat{ABx}(Với số đo các góc theo câu b.)d. Trên cạnh AB lấy điểm E (E ko trùng với A và B). Chứng minh rằng 2 đoạn thẳng BD và CE cắt nhau.
Đọc tiếp
Cho \(\Delta ABC\)có\(\widehat{ABC}=55^o\), trên cạnh AC lấy điểm D (D ko trùng với A và C)
a. Tính độ dài AC, biết AD=4cm, CD=3cm.
b. Tính số đo của\(\widehat{DBC}\), biết \(\widehat{ABD}=30^o\).
c. Từ B dựng tia Bx sao cho \(\widehat{DBx}=90^o\). Tính số đo \(\widehat{ABx}\)(Với số đo các góc theo câu b.)
d. Trên cạnh AB lấy điểm E (E ko trùng với A và B). Chứng minh rằng 2 đoạn thẳng BD và CE cắt nhau.
Cho \(\Delta ABC\) có AB>AC và \(\widehat{A}=\alpha\). Đường thẳng đi qua A vuông góc với phân giác của góc A cắt đường thẳng BC tại M sao cho BM=BA+Ac. Tính số đo của các \(\widehat{B}\)và \(\widehat{C}\)
Cho \(\Delta ABC\) có \(\widehat{A}=75^0\) , AB = 10cm. Số đo các góc B : C tỉ lệ với 4 : 3. Tính độ dài các cạnh AC; BC và \(S_{ABC}\) .
cho tam giác ABC có \(\widehat{A}\)khác 90\(^o\),\(\widehat{B}\)và\(\widehat{C}\) nhọn, đường cao AH. Vẽ các điểm D,E sao cho AB là trung trực của HD, AC là trung trực của HE. Gọi I,K lần lượt là giao điểm của DE với AB và AC
a, Chứng minh: tam giac ADE cân tại A
b, Tính số đo các góc AIC và AKB
cho tam giác ABC có \(\widehat{A}\)khác 90\(^o\),\(\widehat{B}\)và\(\widehat{C}\) nhọn, đường cao AH. Vẽ các điểm D,E sao cho AB là trung trực của HD, AC là trung trực của HE. Gọi I,K lần lượt là giao điểm của DE với AB và AC
a, Chứng minh: tam giac ADE cân tại A
b, Tính số đo các góc AIC và AKB
Xem thêm câu trả lời
Cho tam giác ABC vuông tại B và \(\widehat{ACB}=30^0\), tia phân giác góc A cắt cạnh BC tại D. Trên cạnh AC lấy E sao cho : AE = AB.
a) Tính số đo các góc\(\widehat{BAC},\widehat{ADC}\)
b) CM : \(\Delta ABD=\Delta AED\)
c) CM : DE là trung trực của đoạn AC
Bài làm
a) Xét ∆ABC vuông tại B có:
^BAC + ^C = 90°
Hay ^BAC + 30° = 90°
=> ^BAC = 60°
Vì AD là phân giác của góc BAC.
=> ^DAC = 60°/2 = 30°
Xét tam giác ADC có:
^DAC + ^ACD + ^ADC = 180°
Hay 30° + 30° + ^ADC = 180°
=> ^ADC = 180° - 30° - 30°
=> ^ADC = 120°
b) Xét tam giác ABD và tam giác AED có:
AB = AE ( gt )
^BAD = ^EAD ( Do AD phân giác )
Cạnh AD chung.
=> ∆ABD = ∆AED ( c.g.c )
c) Vì ∆ABD = ∆AED ( cmt )
=> ^ABD = ^AED = 90°
=> DE vuông góc với AC tại E (1)
Ta có: ^DAC = ^DCA = 30°
=> ∆DAC cân tại D.
=> AD = DC
Xét tam giác DEA và tam giác DEC có:
Góc vuông: ^DEA = ^DEC ( = 90° )
Cạnh huyền AD = DC ( cmt )
Góc nhọn: ^DAC = ^DCA ( cmt )
=> ∆DEA = ∆DEC ( g.c.g )
=> AE = EC
=> E là trung điểm của AC. (2)
Từ (1) và (2) => DE là trung trực của AC ( đpcm )
Cho Delta ABC có widehat{A}90^o và AB AC. Trên cạnh AC lấy điểm D sao cho AD AB. Trên tia đối của tia AB lấy điểm E sao cho AE AC.a) Chứng minh Delta ABCDelta ADE và DE ACb) Chứng minh DE perpBCc) Biết 4widehat{B}5widehat{C}. Tính widehat{AED}
Đọc tiếp
Cho \(\Delta ABC\) có \(\widehat{A}=90^o\) và AB < AC. Trên cạnh AC lấy điểm D sao cho AD= AB. Trên tia đối của tia AB lấy điểm E sao cho AE= AC.
a) Chứng minh \(\Delta ABC=\Delta ADE\) và DE= AC
b) Chứng minh DE \(\perp\)BC
c) Biết \(4\widehat{B}=5\widehat{C}\). Tính \(\widehat{AED}\)
Xét tam giác vuông ABC và tam giác vuông ADE có :
AB=AD
AC=AE
=> tam giác ABC= tam giác ADE ( 2 cạnh góc vuông )
Đúng 0
Bình luận (0)
Cho tam giác ABC có \(\widehat{A}=60\) độ, đường phân giác của góc B và góc C cắt nhau tại I.
a, Tính số đo góc BIC
b, Tính số đo góc IAC
c, Từ I kẻ đường thẳng // với AB cắt AC tại M. \(\Delta AMI\) là tam giác gì?
d, BI, CI cắt AC và AB tại D và E. C/minh: BE + CD = BC
Cho tam giác ABC có widehat{A}110^o,M là trung điểm của BC. Trên tia đối của tia MA lấy điểm K sao cho MKMA.a) Tính số đo của góc ACK.b) Vẽ về phía ngoài của tam giác ABC các đoạn thẳng AD, AE sao cho AD vuông góc với AB và ADAB,AE vuông góc với AC và AEAC. Chứng minh rằng Delta CAKDelta AED.c) Chứng minh rằng MA vuông góc với DECác bn giúp mk nha.
Đọc tiếp
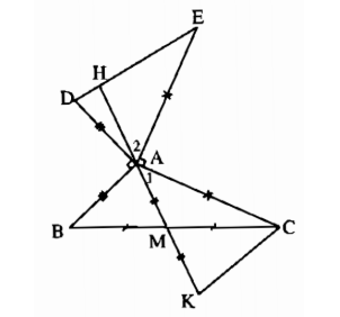
Cho tam giác ABC có \(\widehat{A}=110^o\),M là trung điểm của BC. Trên tia đối của tia MA lấy điểm K sao cho MK=MA.
a) Tính số đo của góc ACK.
b) Vẽ về phía ngoài của tam giác ABC các đoạn thẳng AD, AE sao cho AD vuông góc với AB và AD=AB,AE vuông góc với AC và AE=AC. Chứng minh rằng \(\Delta CAK=\Delta AED.\)
c) Chứng minh rằng MA vuông góc với DE
Các bn giúp mk nha.
a) \(\Delta\)ABM = \(\Delta\)KCM (c.g.c) => ^ABM = ^KCM (2 góc tương ứng) => AB // CK (2 góc so le trong bằng nhau)
=> ^BAC + ^ACK = 1800 (2 góc trong cùng phía) => ^ACK = 1800 - 1100 = 700
b) \(\Delta\)ABM = \(\Delta\)KCM (cmt) => AB = KC (2 cạnh tương ứng). Mà AB = AD => CK = AD
Ta có: ^BAC + ^BAD + ^CAE + ^DAE = 3600 => ^BAC + ^DAE = 1800
Mà ^BAC + ^ACK = 1800 => ^DAE = ^ACK hay ^DAE = ^KCA
Xét \(\Delta\)CAK và \(\Delta\)AED có: CK=AD; CA=AE; ^KCA = ^DAE => \(\Delta\)CAK = \(\Delta\)AED (đpcm).
c) Tia MA giao DE tại điểm H.
\(\Delta\)CAK = \(\Delta\)AED (cmt) => ^CAK = ^AED (2 góc tương ứng) hay ^CAK = ^AEH
Mà ^CAK + ^HAE = 1800 - ^CAE = 900 => ^AEH + ^HAE = 900 => \(\Delta\)AHE vuông tại H
=> AH vuông góc với DE hay MA vuông góc DE (đpcm).
Đúng 0
Bình luận (0)
Cho tam giác ABC có widehat{A}110^0, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm K sao cho MK MA
a) Tính số đo của góc ACK
b) Vẽ về phía ngoài của tam giác ABC các đoạn thẳng AD, AE sao cho AD vuông góc với AB và AD AB, AE vuông góc với AC và AE AC. Chứng minh rằng Delta CAKDelta AED
c) Chứng minh rằng MA vuông góc với DE
Đọc tiếp
Cho tam giác ABC có \(\widehat{A}=110^0\), M là trung điểm của BC. Trên tia đối của tia MA lấy điểm K sao cho MK = MA
a) Tính số đo của góc ACK
b) Vẽ về phía ngoài của tam giác ABC các đoạn thẳng AD, AE sao cho AD vuông góc với AB và AD = AB, AE vuông góc với AC và AE = AC. Chứng minh rằng \(\Delta CAK=\Delta AED\)
c) Chứng minh rằng MA vuông góc với DE
Lời giải:
a) Chứng minh CK // AB để suy ra
∠ACK = 180° - ∠BAC = 180° - 110° = 70°.
b) ΔCAK = ΔAED (c.g.c)
c) Gọi H là giao điểm của MA và DE.
ΔCAK = ΔAED nên ∠A1 = ∠E.
Ta lại có ∠A1 + ∠A2 = 90° nên ∠A2 + ∠E = 90°.
Do đó MA ⊥ DE.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời