gieo một con súc sắc 4 lần tìm xác suất của biến cố.
A"mặt 4 chấm xuất hiện ít nhất 1 lần "
Gieo một con xúc sắc 4 lần. Tìm xác suất của biến cố
A: “ Mặt 4 chấm xuất hiện ít nhất một lần”
A. P ( A ) = 1 − 5 6 4
B. P ( A ) = 1 − 1 6 4
C. P ( A ) = 3 − 5 6 4
D. P ( A ) = 2 − 5 6 4
Gọi A i là biến cố “ mặt 4 chấm xuất hiện lần thứ i” với i = 1; 2; 3; 4.
Khi đó: A i là biến cố “ Mặt 4 chấm không xuất hiện lần thứ i”
Và P ( A i ¯ ) = 1 − P ( A i ) = 1 − 1 6 = 5 6
Ta có: A ¯ là biến cố: “ không có mặt 4 chấm xuất hiện trong 4 lần gieo”
Và A ¯ = A 1 ¯ . A 2 ¯ . A 3 ¯ . A 4 ¯ . Vì các A i ¯ độc lập với nhau nên ta có:
P ( A ¯ ) = P ( A 1 ¯ ) . P ( A 2 ¯ ) . P ( A 3 ¯ ) . P ( A 4 ¯ ) = 5 6 4
Vậy P ( A ) = 1 − P ( A ¯ ) = 1 − 5 6 4 .
Chọn đáp án A.
a. Có 3 mặt nguyên tố: 2,3,5 nên xác suất xuất hiện số nguyên tố ở mỗi lần gieo là \(\dfrac{3}{6}=\dfrac{1}{2}\)
Xác suất 2 lần đều xuất hiện số nguyên tố: \(\dfrac{1}{2}.\dfrac{1}{2}=\dfrac{1}{4}\)
b. Xác suất để lần 1 xuất hiện mặt 6 chấm: \(\dfrac{1}{6}\)
c. Xác suất ít nhất 1 lần xuất hiện mặt 6 chấm: \(\dfrac{2.6-1}{36}=\dfrac{11}{36}\)
d. Xác suất ko lần nào xuất hiện 6 chấm: \(1-\dfrac{11}{36}=\dfrac{25}{36}\)
Gieo một con xúc sắc 4 lần. Tìm xác suất của biến cố A:" Mặt 3 chấm xuất hiện đúng một lần"
Đây giống với xác suất đại học hơn thì phải, cấp 3 hình như người ta ko cho dạng này (công thức Bernoulli)
\(P=C_4^1.\left(\dfrac{1}{6}\right)^1.\left(\dfrac{5}{6}\right)^{4-1}\)
Gieo một con xúc sắc 4 lần. Tìm xác suất của biến cố B: “ Mặt 3 chấm xuất hiện đúng một lần”
A. P ( A ) = 5 324
B. P ( A ) = 5 32
C. P ( A ) = 3 − 5 6 4
D. P ( A ) = 2 − 5 6 4
Gọi B i là biến cố “ mặt 3 chấm xuất hiện lần thứ i” với i =1;2; 3; 4
Khi đó: B i ¯ là biến cố “ Mặt 3 chấm không xuất hiện lần thứ i”
Ta có: A = B 1 ¯ . B 2 . B 3 . B 4 ∪ B 1 . B 2 ¯ . B 3 . B 4 ∪ B 1 . B 2 . B 3 ¯ . B 4 ∪ B 1 . B 2 . B 3 . B 4 ¯
Suy ra :
P A = P B 1 P B 2 P B 3 P B 4 + P B 1 P B 2 P B 3 P B 4 + P B 1 P B 2 P B 3 P B 4 + P B 1 P B 2 P B 3 P B 4
Mà : P ( B i ) = 1 6 ⇒ P ( B i ¯ ) = 1 − 1 6 = 5 6 .
Do đó: P ( A ) = 4. 1 6 3 . 5 6 = 5 324 .
Chọn đáp án A
Gieo một con súc sắc ba lần. Tính xác suất sao cho mặt sáu chấm xuất hiện ít nhất một lần
Không gian mẫu là kết quả của việc gieo 3 lần súc sắc
⇒ n(Ω) = 6.6.6 = 216.
A: “ Mặt 6 chấm xuất hiện ít nhất 1 lần”
⇒ A−: “ Không xuất hiện mặt 6 chấm”
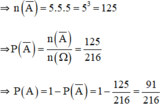
Gieo một con súc sắc cân đối và đồng chất hai lần liên tiếp. Tính xác suất để 1) lần thứ nhất được số chấm chẵn và lần thứ hai được số chấm lẻ. 2) hai lần gieo có số chấm như nhau. 3) mặt 6 chấm xuất hiện ít nhất một lần. 4) tổng số chấm xuất hiện trong hai lần gieo bé hơn 10.
Xác suất:
a. \(\dfrac{3}{6}.\dfrac{3}{6}=\dfrac{1}{4}\)
b. \(\dfrac{6}{36}=\dfrac{1}{6}\)
c. Xác suất mặt 6 chấm ko xuất hiện lần nào: \(\dfrac{5}{6}.\dfrac{5}{6}=\dfrac{25}{36}\)
Xác suất mặt 6 xuất hiện ít nhất 1 lần: \(1-\dfrac{25}{36}=\dfrac{11}{36}\)
d. Các trường hợp tổng 2 mặt lớn hơn hoặc bằng 10: (6;4), (4;6); (5;5); (5;6);(6;5);(6;6) có 6 khả năng
\(\Rightarrow36-6=30\) khả năng tổng số chấm bé hơn 10
Xác suất: \(\dfrac{30}{36}=\dfrac{5}{6}\)
Gieo một con súc sắc 3 lần. Tính xác suất sao cho mặt 6 chấm xuất hiện ít nhất một lần ?
Gieo một súc sắc 3 lần
a) Tính xác suất để có ít nhất một lần xuất hiện mặt 6 chấm
A. 1/216
B. 91/216
C. 7/216
D. 25/72
Gọi Ai là biến cố:” xuất hiện mặt sáu chấm ở lần thứ i”, i=1,2,3 X là biến cố:” có ít nhất một lần xuất hiện mặt thứ 6” thì
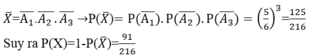
Chọn B
Một con súc sắc cân đối và đồng chất được gieo hai lần. Tính xác suất sao cho :
a) Tổng số chấm của hai lần gieo là 6
b) Ít nhất một lần gieo xuất hiện mặt một chấm
Rõ ràng \(\Omega=\left\{\left(i;j\right):1\le i,j\le6\right\}\)
Kí hiệu :
\(A_1:\) "Lần đầu xuất hiện mặt 1 chấm"
\(B_1:\) "Lần thứ hai xuất hiện mặt 1 chấm"
\(C:\) " Tổng số chấm là 6"
\(D:\) "Mặt 1 chấm xuất hiện ít nhất một lần"
a) Ta có \(C=\left\{\left(1,5\right),\left(5,1\right),\left(2,4\right),\left(4,2\right)\left(3,3\right)\right\},P\left(C\right)=\dfrac{5}{36}\)
b) Ta có \(A_1,B_1\) độc lập và \(D=A_1\cup B_1\) nên
\(P\left(D\right)=P\left(A_1\right)+P\left(B_1\right)-P\left(A_1B_1\right)\)
\(=\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{6}.\dfrac{1}{6}=\dfrac{11}{36}\)
Khi gieo con súc sắc 1 lần xác suất để xuất hiện mặt 1 chấm là 1/6. Gieo
con súc sắc 250 lần. Tính xác suất để trong 250 lần gieo đó mặt 1 chấm xuất hiện từ 45 đến 49
lần