tìm tất cả các giá trị của m để phương trình sinx=2m có 2 nghiệm phân biệt trên đoạn 0; \(\pi\)
QD
Những câu hỏi liên quan
Tìm tất cả các giá trị của tham số m để phương trình
1
3
cos
3
x
−
3
cos
2
x
+
5
cos
x
−
3
+
2
m
0
có đúng bốn nghiệm phân biệt thuộc đoạn
0
;...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để phương trình 1 3 cos 3 x − 3 cos 2 x + 5 cos x − 3 + 2 m = 0
có đúng bốn nghiệm phân biệt thuộc đoạn 0 ; 2 π .
A. − 3 2 < m < − 1 3
B. 1 3 ≤ m < 3 2
C. 1 3 < m < 3 2
D. − 3 2 ≤ m ≤ − 1 3
Chọn C.
Phương pháp:
Giải phương trình bằng phương pháp đặt ẩn phụ.
Cách giải:

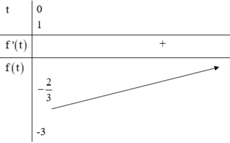
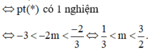
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình
4
x
−
2
m
.2
x
+
m
+
2
0
có 2 nghiệm phân biệt. A.
−
2
m
2
B.
m
−
2
C. m 2 D. m 2
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 4 x − 2 m .2 x + m + 2 = 0 có 2 nghiệm phân biệt.
A. − 2 < m < 2
B. m > − 2
C. m > 2
D. m < 2
Đáp án C
Phương pháp:
Đặt 2 x = t t > 0 , đưa về phương trình bậc 2 ẩn t, tìm điều kiện của phương trình bậc 2 ẩn t để phương trình ban đầu có 2 nghiệm phân biệt.
Cách giải: Đặt 2 x = t t > 0 khi đó phương trình trở thành t 2 − 2 m t + m + 2 = 0 *
Để phương trình ban đầu có 2 nghiệm phân biệt thì phương trình (*) có 2 nghiệm dương phân biệt.
Khi đó: Δ ' > 0 S > 0 P > 0 ⇔ m 2 − m − 2 > 0 2 m > 0 m + 2 > 0 ⇔ m > 2 m < − 1 m > 0 m > − 2 ⇒ m > 2
Chú ý và sai lầm: Rất nhiều học sinh sau khi đặt ẩn phụ thì quên mất điều kiện t > 0, dẫn đến việc chỉ đi tìm điều kiện đề phương trình (*) có 2 nghiệm phân biệt.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số thực m để phương trình
4
x
−
2
m
.2
x
−
2
m
+
3
0
có hai nghiệm phân biệt? A.
1
m
3
2
B. m 0 C. m 1
m
−
3
h
o
ặ
c
m
...
Đọc tiếp
Tìm tất cả các giá trị của tham số thực m để phương trình 4 x − 2 m .2 x − 2 m + 3 = 0 có hai nghiệm phân biệt?
A. 1 < m < 3 2
B. m > 0
C. m > 1 m < − 3 h o ặ c m > 1
D. m < − 3 h o ặ c m > 1
Tìm tất cả các giá trị của m để phương trình \(sin2x=2m\) có hai nghiệm phân biệt trên đoạn \(\left[0;\pi\right]\)
A. \(0\le x< \dfrac{1}{2}\) B. \(0\le x< 1\) C. \(0\le x\le\dfrac{1}{2}\) D. \(0\le x\le1\)
Không có đáp án đúng. Theo đáp án thì $m=0$ thì $\sin 2x=2m$ có 2 nghiệm pb thuộc $[0;\pi]$
Tức là $\sin 2x=0$ có 2 nghiệm pb $[0;\pi]$. Mà pt này có 3 nghiệm lận:
$x=0$
$x=\frac{1}{2}\pi$
$x=\pi$
Đúng 0
Bình luận (0)
1, cho phương trình sin2x-left(2m+sqrt{2}right)left(sinx+cosxright)+2msqrt{2}+10 tìm các giá trị m để phương trình có đúng 2 nghiệm xinleft(0;dfrac{5Pi}{4}right)2,tìm tất cả các giá trị thực của tham số m để phương trình cos2x+left(2m+1right)sinx-m-10 có đúng 2 nghiệm thuộc khoảng left(dfrac{Pi}{2};dfrac{3Pi}{2}right)3, cho phương trình cos^2x-2mcosx+6m-90 tìm các giá trị m để phương trình có nghiệm thuộc khoảng left(-dfrac{Pi}{2};dfrac{Pi}{2}right)
Đọc tiếp
1, cho phương trình \(sin2x-\left(2m+\sqrt{2}\right)\left(sinx+cosx\right)+2m\sqrt{2}+1=0\) tìm các giá trị m để phương trình có đúng 2 nghiệm \(x\in\left(0;\dfrac{5\Pi}{4}\right)\)
2,tìm tất cả các giá trị thực của tham số m để phương trình \(cos2x+\left(2m+1\right)sinx-m-1=0\) có đúng 2 nghiệm thuộc khoảng \(\left(\dfrac{\Pi}{2};\dfrac{3\Pi}{2}\right)\)
3, cho phương trình \(cos^2x-2mcosx+6m-9=0\) tìm các giá trị m để phương trình có nghiệm thuộc khoảng \(\left(-\dfrac{\Pi}{2};\dfrac{\Pi}{2}\right)\)
Tìm tất cả các giá trị của tham số m để phương trình
9
x
−
2
m
+
1
3
x
+
m
+
1
0
có hai nghiệm phân biệt. A.
m
3
2
B.
m
−
3...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để phương trình 9 x − 2 m + 1 3 x + m + 1 = 0 có hai nghiệm phân biệt.
A. m > 3 2
B. m < − 3 2
C. m > − 1 2
D. m > − 1
Tìm tất cả các giá trị thực của tham số m để phương trình
x
3
-
3
x
+
2
m
0
có ba nghiệm thực phân biệt A.
m
∈
-
2
;
2
B.
-
1
;
1
C.
-...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình x 3 - 3 x + 2 m = 0 có ba nghiệm thực phân biệt
A. m ∈ - 2 ; 2
B. - 1 ; 1
C. - ∞ ; - 1 ∪ 1 ; + ∞
D. - 2 ; + ∞
Tìm tất cả các giá trị thực của tham số m để phương trình
x
3
−
3
x
+
2
m
0
có ba nghiệm thực phân biệt. A.
m
∈
−
2
;
2
B.
m
∈
−
1
;
1...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình x 3 − 3 x + 2 m = 0 có ba nghiệm thực phân biệt.
A. m ∈ − 2 ; 2
B. m ∈ − 1 ; 1
C. m ∈ − ∞ ; − 1 ∪ 1 ; + ∞
D. m ∈ − 2 ; + ∞
Đáp án B
Xét y = x 3 − 3 x
Ta có: y’= 3 x 2 − 3
y’= 0 ó x = -1 hoặc x = 1
Ta có bảng biến thiên
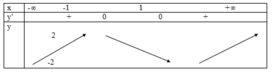
Vậy đường thẳng y = -2m cắt đồ thị hàm số y = x 3 − 3 x tại 3 điểm phân biệt
ó -2<-2m<2 ó m ∈ ( − 1 ; 1 )
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để phương trình
4
x
-
2
x
-
2
m
+
1
0
có hai nghiệm âm phân biệt.
Đọc tiếp
Tìm tất cả các giá trị của tham số m để phương trình 4 x - 2 x - 2 m + 1 = 0 có hai nghiệm âm phân biệt.
![]()
![]()
![]()
![]()





