Làm tính chia:
\(\left(6x^3-7x^2-x+2\right):\left(2x+1\right)\)
Làm tính chia :
a) \(\left(6x^3-7x^2-x+2\right):\left(2x+1\right)\)
b) \(\left(x^4-x^3+x^2+3x\right):\left(x^2-2x+3\right)\)
c) \(\left(x^2-y^2+6x+9\right):\left(x+y+3\right)\)
a) \(\left( {6{x^3} - 7{x^2} - x + 2} \right):\left( {2x + 1} \right)\)

b) $(x^4-x^3+x^2+3x):(x^2-2x+3)$

c) \(\left( {{x^2} + {y^2} + 6x + 9} \right):\left( {x + y + 3} \right)\)
\(=\left( {{x^2} + 6x + 9 - {y^2}} \right)\left( {x + y + 3} \right)\)
\(=\left[ {\left( {{x^2} + 2x.3 + {3^2}} \right) - {y^2}} \right]:\left( {x + y + 3} \right)\)
\(=\left[ {{{\left( {x + 3} \right)}^2} - {y^2}} \right]:\left( {x + y + 3} \right)\)
\(=\left( {x + 3 - y} \right)\left( {x + 3 + y} \right):\left( {x + y + 3} \right)\)
$= x + 3 - y$
$= x - y + 3$
(6x3 - 7x2 - x + 2) : (2x + 1)
= (6x3 + 3x2 - 10x2 - 5x + 4x + 2) : (2x + 1)
= [(6x3 + 3x2) - (10x2 + 5x) + (4x + 2)] : (2x + 1)
= [3x2(2x + 1) - 5x(2x + 1) + 2(2x + 1)] : (2x + 1)
= (3x2 - 5x + 2)(2x + 1) : (2x + 1)
= 3x2 - 5x + 2
(x4 - x3 + x2 + 3x) : (x2 - 2x + 3)
= (x4 + x3 - 2x3 - 2x2 + 3x2 + 3x) : (x2 - 2x + 3)
= [(x4 + x3) - (2x3 + 2x2) + (3x2 + 3x)] : (x2 - 2x + 3)
= [x3(x + 1) - 2x2(x + 1) + 3x(x + 1)] : (x2 - 2x + 3)
= (x3 - 2x2 + 3x)(x + 1) : (x2 - 2x + 3)
= x(x2 - 2x + 3)(x + 1): (x2 - 2x + 3)
= x(x + 1)
= x2 + x
(x2 - y2 + 6x + 9) : (x + y + 3)
= [(x2 + 6x + 9) - y2] : (x + y + 3)
= [(x + 3)2 - y2] : (x + y + 3)
= (x + 3 + y)(x + 3 - y) : (x + y + 3)
= (x + y + 3)(x - y + 3) : (x + y + 3)
= x - y + 3
CHÚC BN HOK TỐT ![]()
![]()
![]()
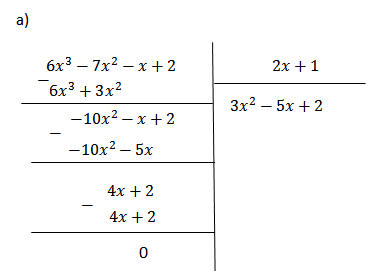
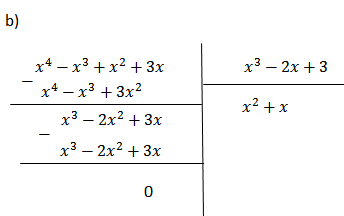
c) (x2+y2+6x+9):(x+y+3)
= (x2+6x+9−y2)(x+y+3)
= [(x2+2x.3+32)−y2]:(x+y+3)
= [(x+3)2−y2]:(x+y+3)
= (x+3−y)(x+3+y):(x+y+3)
= x + 3 - y
= x - y + 3
Làm tích chia:
\(\left(6x^3-7x^2-x+2\right):\left(2x+1\right)\)
\(=\left(6x^3-7x^2-x+2\right).\frac{1}{2x+1}\)
Tính:
\(a)\left(-2x^2\right)\cdot\left(3x-4x^3+7-x^2\right)\)
\(b)\left(x+3\right)\cdot\left(2x^2-3x-5\right)\)
\(c)\left(-6x^5+7x^4-6x^3\right):3x^3\)
\(d)\left(9x^2-4\right):\left(3x+2\right)\)
\(e)\left(2x^4-13x^3+15x^2+11x-3\right):\left(x^2-4x-3\right)\)
a: \(=-2x^2\cdot3x+2x^2\cdot4X^3-2x^2\cdot7+2x^2\cdot x^2\)
\(=8x^5+2x^4-6x^3-14x^2\)
b: \(=2x^3-3x^2-5x+6x^2-9x-15\)
\(=2x^3+3x^2-14x-15\)
c: \(=\dfrac{-6x^5}{3x^3}+\dfrac{7x^4}{3x^3}-\dfrac{6x^3}{3x^3}=-2x^2+\dfrac{7}{3}x-2\)
d: \(=\dfrac{\left(3x-2\right)\left(3x+2\right)}{3x+2}=3x-2\)
e: \(=\dfrac{2x^4-8x^3-6x^2-5x^3+20x^2+15x+x^2-4x-3}{x^2-4x-3}\)
=2x^2-5x+1
Làm tính chia
\(1.\left(6x^3-7x^2-x+2\right):\left(2x+2\right)\)
\(2.\left(x^2-y^2+6x-9\right):\left(x+y+3\right)\)
\(3.\left(x^4-x-14\right):\left(2x-5\right)\)
1: \(\dfrac{6x^3-7x^2-x+2}{2x+2}\)
\(=\dfrac{6x^3+6x^2-13x^2-13x+12x+12-10}{2x+2}\)
\(=\dfrac{3x^2\left(2x+2\right)-\dfrac{13}{2}x\left(2x+2\right)+6\left(2x+2\right)-10}{2x+2}\)
\(=3x^2-\dfrac{13}{2}x+6-\dfrac{5}{x+1}\)
2: \(\dfrac{x^2-y^2+6x-9}{x+y+3}\)
\(=\dfrac{x^2-\left(y-3\right)^2}{x+y+3}\)
\(=\dfrac{\left(x-y+3\right)\left(x+y-3\right)}{x+y+3}\)
Tính:
a) \(\left(6x^3-7x^2-x+2\right):\left(2x+1\right)\)
b) \(\left(2x^2-21x^2+67x-60\right):\left(x-5\right)\)
\(a,=\left(6x^3+3x^2-10x^2-5x+4x+2\right):\left(2x+1\right)\\ =\left[3x^2\left(2x+1\right)-5x\left(2x+1\right)+2\left(2x+1\right)\right]:\left(2x+1\right)\\ =3x^2-5x+2\\ b,Sửa:\left(2x^3-21x^2+67x-60\right):\left(x-5\right)\\ =\left(2x^3-10x^2-11x^2+55x+12x-60\right):\left(x-5\right)\\ =\left[2x^2\left(x-5\right)-11x\left(x-5\right)+12\left(x-5\right)\right]:\left(x-5\right)\\ =2x^2-11x+12\)
LÀM TÍNH CHIA:
a) \(\left(6x^6+2x^5-2x^4-15x^3+x^2+7x+2\right):\left(3x^2+x-1\right)\)
b) \(\left(-6x^4+5x^3+17x^2-23x+7\right):\left(-3x^2-2x+7\right)\)
Làm tính chia :
a) \(\left(2x^5-5x^3+x^2+3x-1\right):\left(x^2-1\right)\)
b) \(\left(5x^5-2x^4-9x^3+7x^2-18x-3\right):\left(x^2-3\right)\)
Rút gọn
a, \(\left(x-2\right)^3-\left(x+1\right)^3+2.\left(x-3\right)^2+x-2\)
b, \(\left(2x-5\right).\left(2x+5\right)-\left(2x-3\right)^2\)
c, \(\left(x-7\right).\left(x^2+7x+49\right)-x.\left(x^2+3\right)+256
\)
d, \(\left(2x+3\right).\left(4x^2-6x+9\right)-x.\left(x-1\right).\left(x+1\right)\)
Trình bày cách làm nữa nha . làm dc bao nheieu câu cứ làm nha
Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi làm phép chia :
a) \(\left(x^3-7x+3-x^2\right):\left(x-3\right)\)
b) \(\left(2x^4-3x^3-3x^2-2+6x\right):\left(x^2-2\right)\)
a) (x3 – 7x + 3 – x2) : (x – 3)

b) (2x4 – 3x2 – 3x2 – 2 + 6x) : (x2 – 2)

Xem thêm tại: http://loigiaihay.com/bai-67-trang-31-sgk-toan-8-tap-1-c43a4815.html#ixzz4ensEy1dY
Làm tính chia :
a) \(\left(2x^3+5x^2-2x+3\right):\left(2x^2-x+1\right)\)
b) \(\left(2x^3-5x^2+6x-15\right):\left(2x-5\right)\)
c) \(\left(x^4-x-14\right):\left(x-2\right)\)