Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 sin x + c os 2 x trên đoạn 0 ; π . Khi đó 2 M + m bằng
A. 4
B. 5 2
C. 7 2
D. 5
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 sin x + c os 2 x trên đoạn 0 ; π . Khi đó 2 M + m bằng
A. 4
B. 5 2
C. 7 2
D. 5
Đáp án A
Ta có: y = 2 s i nx+cos 2 x
= 2 sin x + 1 − 2 sin 2 x → t → s inx y = f x = − 2 t 2 + 2 t + 1.
Với x ∈ 0 ; π ⇒ t ∈ 0 ; 1 .
Xét hàm số f t = − 2 t 2 + 2 t + 1 trên 0 ; 1 có f ' t = − 4 t + 2.
Ta có: f ' t = 0 ⇔ t = 1 2 .
Tính f 0 = 1 ; f 1 2 = 3 2 ; f 1 = 1.
Vậy M = 3 2 m = 1 ⇒ 2 M + m = 4.
Tìm giá trị lớn nhất của hàm số y = x + cos 2 x trên đoạn 0 ; π
A. m a x 0 ; π y = 3 π + 2 4
B. m a x 0 ; π y = π + 1
C. m a x 0 ; π y = π - 2 4
D. m a x 0 ; π y = π + 2 4
Tìm giá trị lớn nhất của hàm số y = x + cos 2 x trên đoạn [0; π ]
A.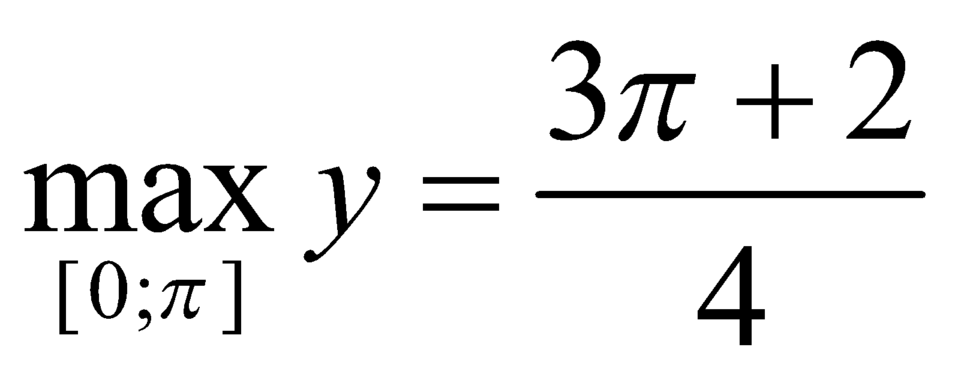
B. ![]()
C. 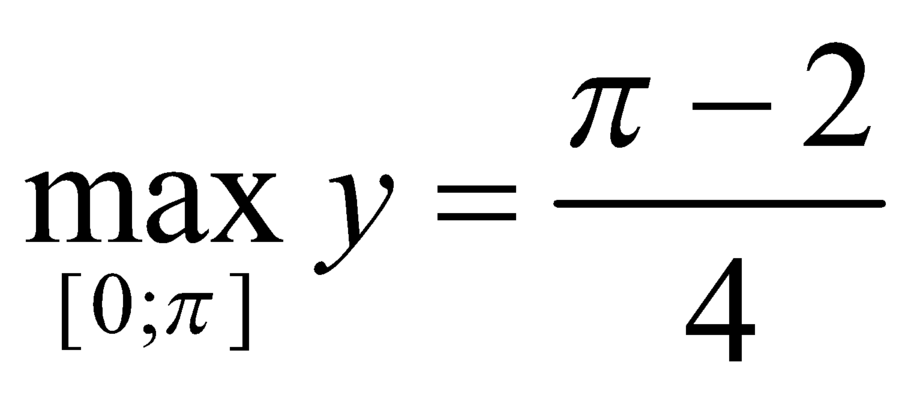
D. 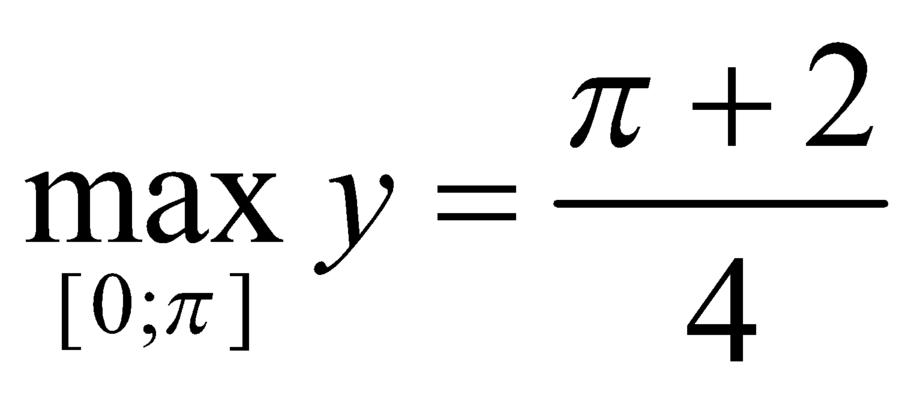
Giá trị nhỏ nhất và lớn nhất của hàm số y = 2 sin x + cos x + 1 sin x - cos 2 x + 3 lần lượt là:
A. – 1/2 và 2
B. 1/2 và 2
C. -2 và -1/2
D. -2 và 1/2
Chọn A
![]()
↔ (2-y)sinx + (1+2y)cosx= 3y-1(*)
Sử dụng điều kiện để phương trình (*) có nghiệm suy ra -1/2 ≤ y ≤ 2
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 3 sin x + 2 sin x + 1 trên đoạn 0 ; π 2 . Khi đó giá trị của M 2 + m 2 là
A. 31 2
B. 11 2
C. 41 4
D. 61 4
Chọn C
Đặt ![]()
Xét hàm ![]() trên đoạn [0;1] có
trên đoạn [0;1] có 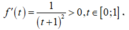
Suy ra hàm số đồng biến trên [0;1]
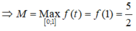 và
và ![]()
Khi đó, 
1/ tìm TXĐ chủa hàm số y = căn 1 - cosx /2 + sinx.
2/ tìm tập giá trị của hàm số y = 2-cos2x.
3/ Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau :
a) y=1 + 2sinx b)y=1 - 2cos^2x
4/ Tìm giá trị nhỏ nhất của hàm số y=tan^2x - 2tanx +3.
1. Không dịch được đề
2.
\(-1\le cos2x\le1\Rightarrow1\le y\le3\)
3.
a. \(-2\le2sinx\le2\Rightarrow-1\le y\le3\)
\(y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
b.
\(0\le cos^2x\le1\Rightarrow-1\le y\le2\)
\(y_{min}=-1\) khi \(cos^2x=1\Rightarrow x=k\pi\)
\(y_{max}=2\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
4.
\(y=\left(tanx-1\right)^2+2\ge2\)
\(y_{min}=2\) khi \(tanx=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: f(x) = 2sinx + sin2x trên đoạn [0; 3 π /2]
f(x) = 2sinx + sin2x trên đoạn [0; 3 π /2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 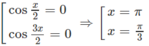
Ta có: f(0) = 0,
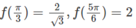
Từ đó ta có: min f(x) = −2 ; max f(x) = 3 3 /2
Gọi M , m theo thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = s inx+ cos 2 x + sin 3 x trên đoạn 0 ; π . Tính P = M + m
A. P = 16 27
B. P = − 19 + 13 13 27
C. P = − 19 − 13 13 27
D. P = − 16 27
GTLN của hàm số y = 2sinx + cos2x trên đoạn [0; π] là
A. 1
B. 3 2
C. 2
D. 7 4
Xét hàm số y=2sin x + cos 2x trên đoạn
y’=2cos x- 2sin 2x = 2cos x(1- 2sin x)
Trên đoạn [0; π]
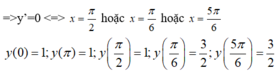
Giá trị lớn nhất của hàm số này trên [0; π] là y = 3 2 .
Chọn B
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 sin x trên đoạn − π 6 ; 5 π 6 . Tính M, m.
A. M = 1 , m = − 1.
B. M = 2 , m = − 2.
C. M = 1 , m = − 2.
D. M = 2 , m = − 1.
Đáp án D.
Ta có y ' = c osx ⇒ y'=0 ⇔ c osx=0 ⇔ x= π 2 + k π k ∈ ℤ ⇒ x 0 = π 2 ∈ − π 6 ; 5 π 6 .
Suy ra y − π 6 = − 1 , y π 2 = 2 , y 5 π 6 = 1 ⇒ M = 2 m = − 1 .