 Các bạn giúp mình làm bài này gấp nhé!
Các bạn giúp mình làm bài này gấp nhé!
NM
Những câu hỏi liên quan
Các bạn giúp mình làm bài này gấp nhé!
\(1,M=\left(\dfrac{\dfrac{2}{5}-\dfrac{2}{9}+\dfrac{2}{11}}{\dfrac{7}{5}-\dfrac{7}{9}+\dfrac{7}{11}}-\dfrac{\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}}{\dfrac{7}{6}-\dfrac{7}{8}+\dfrac{7}{10}}\right)\cdot\dfrac{2013}{2012}\\ M=\left(\dfrac{2\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}{7\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}-\dfrac{\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}}{\dfrac{7}{2}\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}\right)}\right)\cdot\dfrac{2013}{2012}\\ M=\left(\dfrac{2}{7}-\dfrac{2}{7}\right)\cdot\dfrac{2013}{2012}=0\)
\(\left|x^2+\left|x-2\right|\right|=x^2+2021\\ \Leftrightarrow\left[{}\begin{matrix}x^2+\left|x-2\right|=x^2+2021\\x^2+\left|x-2\right|=-x^2-2021\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left|x-2\right|=2021\\\left|x-2\right|=-2x^2-2021\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x-2=\pm2021\\x\in\varnothing\left(-2x^2-2021< 0\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2023\\x=-2019\end{matrix}\right.\)
\(3,\\ A=\left(x-\dfrac{2}{5}\right)^2+\left(y+20\right)^{10}+2022\ge2022\\ A_{min}=2022\Leftrightarrow\left\{{}\begin{matrix}x-\dfrac{2}{5}=0\\y+20=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{5}\\y=-20\end{matrix}\right.\)
Đúng 2
Bình luận (1)
các bạn làm hộ mình bài viết này nhé mình đang cần gấp các bạn giúp mình nhé xin trân trọng cảm ơn các bạn nhìu

Các bạn giúp mình làm bài này nhé mình đang cần gấp cảm ơn các bạn nhìu...

Các bạn giúp mình làm những bài này gấp nhé ! Các bạn biết làm bài nào thì giúp mình bài nấy nhé . Mình cám ơn rất nhiều ^^
Bài 2:
Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow\begin{cases}a=kb\\c=kd\end{cases}\)
=> \(\frac{5a+3b}{5a-3b}=\frac{5kb+3b}{5kb-3b}=\frac{b\left(5k+3\right)}{b\left(5k-3\right)}=\frac{5k+3}{5k-3}\left(1\right)\)
\(\frac{5c+3d}{5c-3d}=\frac{5kd+3d}{5kd-3d}=\frac{d\left(5k+3\right)}{d\left(5k-3\right)}=\frac{5k+3}{5k-3}\left(2\right)\)
Từ (1) và (2) => \(\frac{5a+3b}{5a-3b}=\frac{5c+3d}{5c-3d}\)
Đúng 0
Bình luận (2)
Bài 3:
Đặt \(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=k\)
=> \(\frac{a}{b}.\frac{b}{c}.\frac{c}{d}=k^3\)
=> \(\frac{a}{d}=k^3\) (1)
Lại có: \(\frac{a+b+c}{b+c+d}=\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=k\)
=> \(\left(\frac{a+b+c}{b+c+d}\right)^3=k^3\) (2)
Từ (1) và (2) => \(\frac{a}{d}=\left(\frac{a+b+c}{b+c+d}\right)^3\)
Đúng 0
Bình luận (1)
Bài 1: Ta có:
\(\frac{a+b-c}{c}=\frac{a-b+c}{b}=\frac{-a+b+c}{a}\)
\(=\frac{a+b}{c}-\frac{c}{c}=\frac{a+c}{b}-\frac{b}{b}=\frac{b+c}{a}-\frac{a}{a}\)
\(=\frac{a+b}{c}-1=\frac{a+c}{b}-1=\frac{b+c}{a}-1\)
\(\Rightarrow\frac{a+b}{c}=\frac{a+c}{b}=\frac{b+c}{a}\) (1)
Xét 2 trường hợp
Nếu a + b + c = 0 \(\Rightarrow\begin{cases}a+b=-c\\a+c=-b\\b+c=-a\end{cases}\)\(\Rightarrow\frac{\left(a+b\right).\left(b+c\right).\left(a+c\right)}{abc}=\frac{-c.\left(-b\right).\left(-a\right)}{abc}=-1\)
Nếu a + b + c \(\ne0\)Áp dụng tính chất của dãy tỉ số = nhau ta có:
\(\frac{a+b}{c}=\frac{a+c}{b}=\frac{b+c}{a}=\frac{\left(a+b\right)+\left(a+c\right)+\left(b+c\right)}{c+b+a}=\frac{2.\left(a+b+c\right)}{a+b+c}=2\)
\(\Rightarrow\frac{\left(a+b\right)\left(b+c\right)\left(a+c\right)}{abc}=2^3=8\)
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
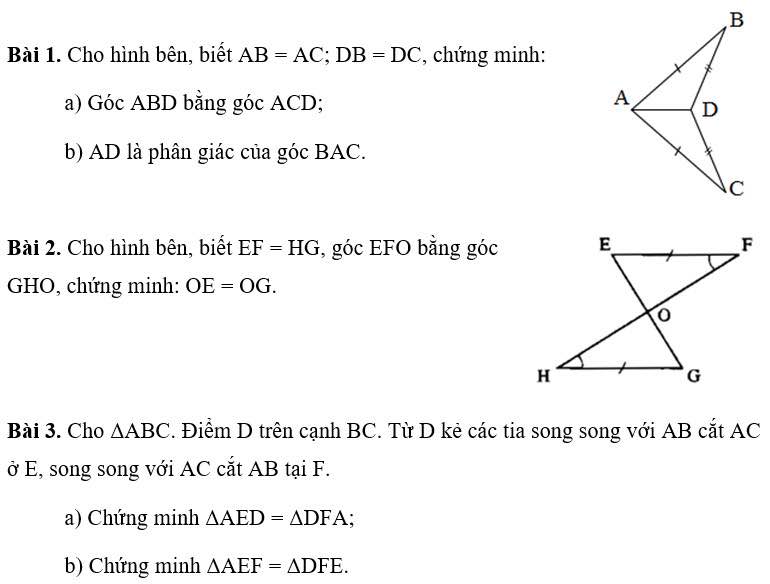 Các bạn làm giúp mình mấy bài này gấp nhé chiều nay mình phải nộp rồi
Các bạn làm giúp mình mấy bài này gấp nhé chiều nay mình phải nộp rồi
Bài 1 :
a,Có \(AD\) chung , mà \(AB=AC;DB=DC\)
\(\Rightarrow\Delta ABC=\Delta ADC\)
Do đó \(\widehat{ABD}=\widehat{ACD}\)
b,\(AD\) là cạnh chung của 2\(\Delta:\Delta ABD,\Delta ACD\)
\(\Rightarrow AD\) là phân giác của \(\widehat{BAC}\)
Bài 2:
Ta có : \(EF=HG,\widehat{EFO}=\widehat{GHO}\)
Theo TH thứ 2 của 2 tam giác bằng nhau ta có : cạnh - góc - cạnh
\(\Rightarrow OE=OG\)
Bài 3: Có hình ko bn ,mk dựa vào hình lm ko mk lười vẽ hình lắm =(((((((
Đúng 2
Bình luận (1)
Các bạn giúp mình câu này gấp nhé!! Ai làm đúng , dễ hiểu mình sẽ tick cho người đó nhé. Các bạn làm nhanh giúp mình nhé. Đề bài như sau:
(X+12) chia hết ( x+3)
Tìm các số tự nhiên x nhé!! Cảm ơn các bạn nhiều
x + 3 + 9 chia hết x + 3
9 chia hết x + 3
x + 3 thuộc Ư ( 9 )
mà Ư (9) = ( 1,3,9 )
hay x + 3 thuộc ( 1,3,9 )
ta có bảng
x + 3 1 3 9
x -2 0 6
ĐG Loại TM TM
Vậy x thuộc ( 0 , 6 )
Đúng 1
Bình luận (0)
||2x-3|-x+1|=4x-1
Các bạn ơi giúp mình bài này nhé !(mình cần gấp lắm)
các bạn nhớ ghi rõ cách làm ra nha!!!!
Các bạn giúp mình bài này gấp nhé mình cảm ơn!
a) Ta có: MN⊥d, EF⊥d
=> MN//EF(từ vuông góc đến song song)
b) Ta có: \(\widehat{MPQ}=180^0-\widehat{MPb}=180^0-55^0=125^0\)(kề bù)
\(\Rightarrow\widehat{MPQ}=\widehat{NMc}=125^0\)
Mà 2 góc này đồng vị
=> PQ//MN
Mà MN//EF
=> PQ//EF
Đúng 1
Bình luận (1)
Các bạn giúp mih bài này nhé ! Mình cần gấp . Cảm ơn
Đọc tiếp
Các bạn giúp mih bài này nhé ! Mình cần gấp . Cảm ơn
a/ \(0,5m=5dm\)
b/ \(45,2cm=4,52dm\)
c/ \(2,43m=24,3dm\)
d/ \(2450mm=24,5dm\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời







