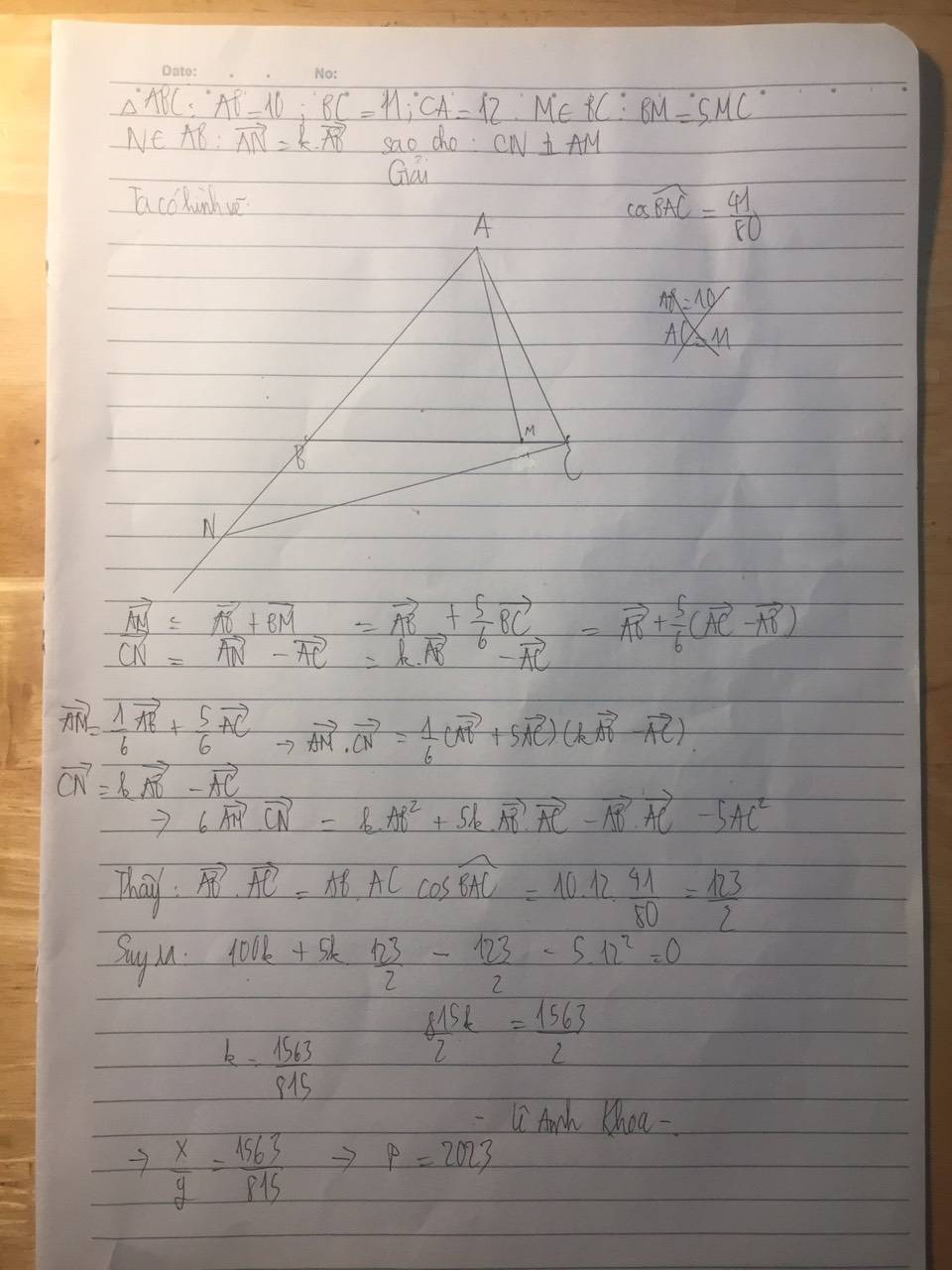
Cho tam giác ABC có M thuộc AB thỏa mãn BM=1/4BA; N là điểm thỏa mãn véctơ 3NA=+ véctơ 2NC= véctơ 0. K là trung điểm MN, H là điểm sao cho 4HB+ 3 HC= véctơ 0. Hãy biểu diễn Véctơ KH theo véctơ AB và véctơ AC
TN
Những câu hỏi liên quan
Cho tam giác ABC vuông ở A, AB < AC; M thuộc cạnh AC sao cho góc ABM =gócACB; điểm D thuộc cạnh AB sao cho CD cắt BM tại E thỏa mãn gócBED = gócACB. CM: CE =1/2AD .
Mong ai đó sẽ trả lời =(
mình cx cần 🥺🥺🥺
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD có AB 2, AD 4, điểm M thuộc cạnh BC thỏa mãn BM 1. Điểm N thuộc đường chéo AC thỏa mãn
A
N
→
x
A
C
→
. Giá trị của x để tam giác AMN vuông tại M là A. 5/8 B. 5/4 C. 5/16 D. 0, 5
Đọc tiếp
Cho hình chữ nhật ABCD có AB = 2, AD = 4, điểm M thuộc cạnh BC thỏa mãn BM = 1. Điểm N thuộc đường chéo AC thỏa mãn A N → = x A C → . Giá trị của x để tam giác AMN vuông tại M là
A. 5/8
B. 5/4
C. 5/16
D. 0, 5
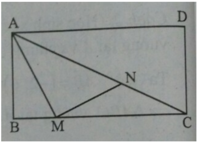
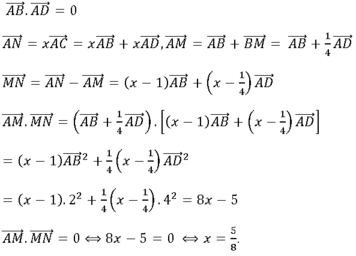
Chọn A.
Chú ý: Nếu có đúng bốn phương án như trong đề thi thì có thể dự đoán ngay phương án A sau khi vẽ hình
Đúng 0
Bình luận (0)
Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của AC, AB. P và Q lần lượt thuộc BM và CN sao cho BP = 1/3BM, CQ = 1/3CN
a) Tứ giác MNPQ là hình gì? vì sao?
b) Tam giác ABC phải thỏa mãn đ/k gì thì thì MNPQ là hình chữ nhật?
c) Tam giác ABC, BM, CN thỏa mãn đk gì thì MNPQ là hình thoi, hình vuông
[Câu hỏi Xuân Quý Mão 2023 - môn Toán]Cho tam giác ABC có AB10;BC11;CA12. Gọi M thuộc cạnh BC thỏa mãn BM 5MC và N thuộc đường thẳng AB sao cho overrightarrow{AN} koverrightarrow{AB}, với kin R. Biết kdfrac{x}{y} (x,yin Z, phân số tối giản) sao cho CNperp AM. Tính giá trị biểu thức: Psqrt{2022x-2023y+2580888}.
Đọc tiếp
[Câu hỏi Xuân Quý Mão 2023 - môn Toán]
Cho tam giác ABC có \(AB=10;BC=11;CA=12.\) Gọi M thuộc cạnh BC thỏa mãn BM = 5MC và N thuộc đường thẳng AB sao cho \(\overrightarrow{AN}\) \(=k\overrightarrow{AB}\), với \(k\in R\). Biết \(k=\dfrac{x}{y}\) (\(x,y\in Z\), phân số tối giản) sao cho \(CN\perp AM\). Tính giá trị biểu thức: \(P=\sqrt{2022x-2023y+2580888}\).
 không biết đúng không, góp thử bài làm heheh
không biết đúng không, góp thử bài làm heheh
Đúng 6
Bình luận (5)
Từ tam giác ABC có AB = 10 ; BC = 11 ; CA = 12
=> \(cosC=\dfrac{AC^2+BC^2-AB^2}{2AC.BC}=\dfrac{11^2+12^2-10^2}{2.11.12}=\dfrac{5}{8}\)
tương tự cosB = \(\dfrac{7}{20}\)
cos A = \(\dfrac{41}{80}\)
Lại có \(CN\perp AM\)
nên \(\overrightarrow{CN}.\overrightarrow{AM}=0\)
\(\Leftrightarrow(\overrightarrow{CA}+\overrightarrow{AN}).(\overrightarrow{AC}+\overrightarrow{CM})=0\)
\(\Leftrightarrow(\overrightarrow{CA}+k\overrightarrow{AB})(\overrightarrow{AC}+\dfrac{1}{5}\overrightarrow{CB})=0\)
\(\Leftrightarrow-AC^2+\dfrac{1}{5}CA.CB.cosC+kAB.AC.cosA+\dfrac{1}{5}k.AB.BC.cos(180^{\text{o}}-B)=0\)
\(\Leftrightarrow-12^2+\dfrac{1}{5}.12.11.\dfrac{5}{8}+k.10.12.\dfrac{41}{80}+\dfrac{1}{5}k.10.11.(-\dfrac{7}{20})=0\)
\(\Leftrightarrow k=\dfrac{1275}{538}=\dfrac{x}{y}\) tối giản => (x ; y) = (1275;538) ; (-1275,-538) (x;y \(\inℤ\))
Với (x,y) = (1275,538)
=> P = \(\sqrt{2022.1275-2023.538+2580888}=\sqrt{4070564}\)
Với (x;y) = (-1275 ; -538)
=> P = \(\sqrt{1091212}\)
Đúng 2
Bình luận (1)
Xem thêm câu trả lời
Cho tam giác ABC có ba đường cao AH, BM, CN thỏa mãn: \(\frac{1}{AH^2}=\frac{1}{BM^2}+\frac{1}{CN^2}\) . Khi đó tam giác ABC là tam giác gì???
Cho tam giác ABC, ba điểm M, N, P lần lượt thuộc BC, CA, AB sao cho BM/BC = CN/CA = AP/AB và BM/BC < 1/2. Chứng minh tam giác ABC và MNP có cùng trọng tâm
Cho tam giác ABC có ba đường cao AH, BM, CN thỏa mãn: \(\frac{1}{AH^2}=\frac{1}{BM^2}+\frac{1}{CN^2}\) . Khi đó tam giác ABC là tam giác gì???
cho tam giác ABC có A=90, BC=2a.
a)Giả sử điểm A thay đổi sao cho BAC=90,BC=2a.Tam giác ABC phải thỏa mãn điều kiện gì để diện tích tam giác AHO lớn nhất
b)gọi O là trung điểm của BC, M là trung điểm của AC, AO cắt BM tại G. Giả sử CG cắt AB tại N. Tứ giác AMON là hình gì? Tam giác ABC phải thỏa mãn điều kiện gì để diện tích tứ giác AMON lớn nhất?
Cho tam giác ABC với ba điểm M,N,P lần lượt thuộc các cạnh BC,CA,AB sao cho BM/BC=CN/CA=AP/AB và BM/BC < 1/2. Chứng minh rằng hai tam giác ABC và tam giác MNP có cùng trọng tâm