Cho tam giác ABC thỏa mãn BC=2AB và \(\widehat{B}=2\widehat{C}\)
CMR tam giác ABC vuông tại A
KK
Những câu hỏi liên quan
Cho tam giác ABC có BC=2AB và \(\widehat{B}=2\widehat{C}\). CMR:tam giác ABC vuông tại A
Cho hai tam giác ABC và A’B’C’ thỏa mãn: BC = B’C’ = 3 cm, \(\widehat B = \widehat {B'} = 60^\circ ,\widehat C = 50^\circ ,\widehat {A'} = 70^\circ \). Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?
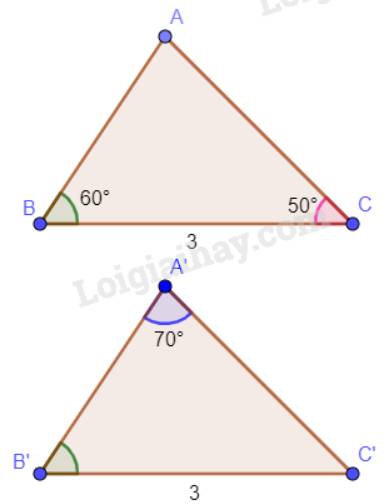
Tổng ba góc trong một tam giác bằng 180°. Vậy trong tam giác A’B’C’ có \(\widehat {C'} = 180^\circ - 70^\circ - 60^\circ = 50^\circ \).
Xét hai tam giác ABC và A’B’C’ có:
\(\widehat B = \widehat {B'} = 60^\circ ;\)
BC = B’C’ ( = 3 cm)
\(\widehat C = \widehat {C'} = 50^\circ \)
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)
Đúng 0
Bình luận (0)
Cho tam giác ABC. \(\widehat{A}\)= 90, BC=2AB. Tia phân giác của \(\widehat{B}\)cắt AC tại D
a, CMR: DB=DC
b, Tính \(\widehat{B}\),\(\widehat{C}\)của tam giác ABC
Cho tam giác ABC thỏa mãn \(\widehat B = \widehat C\). Kẻ AH vuông góc với BC, H thuộc BC (Hình 74).
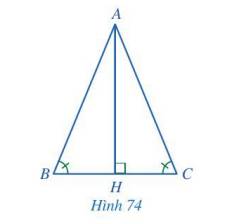
a) \(\widehat B = \widehat C\). Mà tổng ba góc trong một tam giác bằng 180° nên \(\widehat {BAH} = \widehat {CAH}\).
Xét hai tam giác BAH và CAH có:
\(\widehat {BAH} = \widehat {CAH}\);
AH chung;
\(\widehat {AHB} = \widehat {AHC}\) (= 90°).
Vậy \(\Delta BAH = \Delta CAH\)(g.c.g)
b) \(\Delta BAH = \Delta CAH\) nên AB = AC ( 2 cạnh tương ứng).
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A và cạnh BC = 2AB. E là trung điểm của BC. Tia phân giác của \(\widehat{B}\)cắt BC tại D.
a) Chứng minh DB là tia phân giác của \(\widehat{ADE}\)
b) Chứng minh BD = BC
c) Tính \(\widehat{B,}\)\(\widehat{C}\)của tam giác ABC
Cho hai tam giác ABC và A’B’C’ thỏa mãn: AB = A’B’, \(\widehat A = \widehat {A'},\widehat C = \widehat {C'}\). Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?
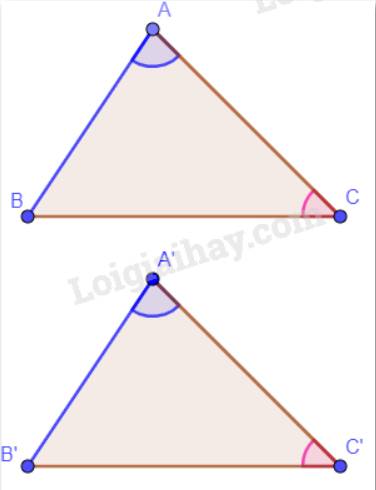
Vì \(\widehat A = \widehat {A'},\widehat C = \widehat {C'}\)mà tổng ba góc trong một tam giác bằng 180° nên \(\widehat B = \widehat {B'}\).
Xét hai tam giác ABC và A’B’C’ có: \(\widehat A = \widehat {A'}\), AB = A’B’, \(\widehat B = \widehat {B'}\).
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)
Đúng 0
Bình luận (0)
H24
10 tháng 1 2021 lúc 20:27
Bài 1: Cho tam giác ABC vuông tại A.CMR: \(m^2_b +m^2_c =5m^2_a\)
Bài 2: Cho tam giác ABC thỏa mãn \(\frac{a^3+b^3-c^3}{a+b-c}=c^2\). Tìm số đo của \(\widehat{C}\)
Bài 3: Nhận dạng tam giác ABC nếu \(\frac{a^3+c^3-b^3}{a+c-b}=b^2\) và \(sinA.sinC=\frac{3}{4}\)
1.
Áp dụng công thức trung tuyến:
\(m_b^2+m_c^2=\dfrac{2a^2+2c^2-b^2}{4}+\dfrac{2a^2+2b^2-c^2}{4}\)
\(=\dfrac{4a^2+b^2+c^2}{4}\)
\(=\dfrac{9a^2+b^2+c^2-5a^2}{4}\)
\(=\dfrac{9\left(b^2+c^2\right)+b^2+c^2-5a^2}{4}\)
\(=5\left(\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}\right)=5m_a\)
Đúng 0
Bình luận (0)
Cho tam giác ABC thỏa mãn điều kiện \(\widehat{A}=2\widehat{B}=4\widehat{C}\)
Chứng minh rằng: \(\dfrac{1}{AB}=\dfrac{1}{AC}+\dfrac{1}{BC}\)
Cho tam giác ABC thỏa mãn : \(2.\widehat{B}+3.\widehat{C}=180\) CMR: \(BC^2=BC.AC+AB^2\)