CM nếu (a^2+b^2) .(x^2+y^2)=(ax+by)^2 thì ay-bx=0
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
BD
Những câu hỏi liên quan
cm nếu: (a2 + b2).(x2 + y2) = (ax + by)2 với mọi x khác 0 thì ay = bx
Ta có : (a^2 + b^2)(x^2 + y^2) = (ax + by)^2
=> a^2x^2 + a^2y^2 +B^2x^2 + b^2y^2 = a^2x^2 + b^2y^2 + 2axby
=> chuyển vế trái sang phải: a^2x^2 + a^2y^2 + b^2x^2 + b^2y^2 - a^2x^2 - b^2y^2 - 2axby = 0
=> a^2y^2 + b^2x^2 - 2axby = 0
=> (ax - by)^2 = 0
Chỉ khi ax = by thì (ax - by)^2 = 0 => ax = by.
Đúng 0
Bình luận (0)
Chứng minh rằng nếu (a^2+b^2)(x^2+y^2)=(ax+by)^2 thì ay-bx=0
Ta có : \(\left(a^2+b^2\right)\left(x^2+y^2\right)=\left(ax+by\right)^2\)
\(\Leftrightarrow a^2x^2+a^2y^2+b^2x^2+b^2y^2=a^2x^2+b^2y^2+2axby\)
\(\Leftrightarrow\left(ay\right)^2-2.ay.bx+\left(bx\right)^2=0\)
\(\Leftrightarrow\left(ay-bx\right)^2=0\Leftrightarrow ay-bx=0\)
Vậy ta có điều phải chứng minh.
Đúng 0
Bình luận (1)
Chứng minh rằng nếu (a2 +b 2)(x2+y2) = (ax + by )2 thì ay- bx=0
Cho biết : (a^2 + b^2) * (x^2 + y^2)= (ax + by) . CM ay=bx
Lời giải:
\((a^2+b^2)(x^2+y^2)=(ax+by)^2\)
\(\Leftrightarrow a^2x^2+a^2y^2+b^2x^2+b^2y^2=a^2x^2+2axby+b^2y^2\)
\(\Leftrightarrow a^2y^2-2axby+b^2x^2=0\)
\(\Leftrightarrow (ay)^2-2(ay)(bx)+(bx)^2=0\)
\(\Leftrightarrow (ay-bx)^2=0\Rightarrow ay=bx\) (đpcm)
Đúng 0
Bình luận (0)
bn nào viết rõ hơn giùm mik đc ko.
(a^2+b^2)(x^2+y^2)=(ax+by)^2
<=> a^2x^2 + a^2y^2 + b^2x^2 + b^2y^2 = a^2x^2 + 2abxy + b^2y^2
<=> a^2y^2 + b^2x^2 = 2abxy
<=> a^2y^2 + b^2x^2 - 2abxy = 0
<=> (ay - bx)^2 = 0
=> ay - bx = 0
=> ay = bx
=> a/x = b/y ( x,y khác 0)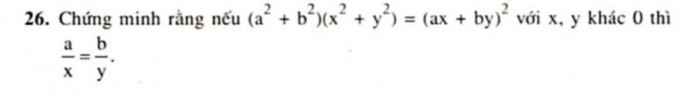
Ta có: \(\left(ax+by\right)^2=\left(a^2+b^2\right)\left(x^2+y^2\right)\)
\(\Leftrightarrow a^2x^2+2abxy+b^2y^2=a^2x^2+a^2y^2+x^2b^2+b^2y^2\)
\(\Leftrightarrow2abxy=a^2y^2+x^2b^2\)
\(\Leftrightarrow\left(ay-xb\right)^2=0\)
\(\Leftrightarrow ay=xb\)
hay \(\dfrac{a}{x}=\dfrac{b}{y}\)
Đúng 1
Bình luận (0)
1,CMR nếu a,b,c x,y,z thỏa mãn điều kiện :frac{bz+cy}{xleft(-ax+by+czright)}frac{cx+az}{yleft(ax-by+czright)}frac{ay+bx}{zleft(ax+by-czright)}thì frac{x}{aleft(b^2+c^2-a^2right)}frac{y}{bleft(a^2+c^2-b^2right)}frac{z}{cleft(a^2+b^2-c^2right)}( giả thiết các tỉ số đều có nghĩa )2,CMR nếu frac{a+bx}{b+cy}frac{b+cx}{c+ay}frac{c+ax}{a+by}thì a^3+b^3+c^3-3abc03,CMR nếu x+frac{1}{y}y+frac{1}{z}z+frac{1}{x}thì xyz hoặc x2y2z21
Đọc tiếp
1,CMR nếu a,b,c x,y,z thỏa mãn điều kiện :
\(\frac{bz+cy}{x\left(-ax+by+cz\right)}=\frac{cx+az}{y\left(ax-by+cz\right)}=\frac{ay+bx}{z\left(ax+by-cz\right)}\)
thì \(\frac{x}{a\left(b^2+c^2-a^2\right)}=\frac{y}{b\left(a^2+c^2-b^2\right)}=\frac{z}{c\left(a^2+b^2-c^2\right)}\)
( giả thiết các tỉ số đều có nghĩa )
2,CMR nếu \(\frac{a+bx}{b+cy}=\frac{b+cx}{c+ay}=\frac{c+ax}{a+by}\)
thì \(a^3+b^3+c^3-3abc=0\)
3,CMR nếu \(x+\frac{1}{y}=y+\frac{1}{z}=z+\frac{1}{x}\)
thì x=y=z hoặc x2y2z2=1
Chứng minh rằng nếu ( a2 + b2 )( x2 + y2 ) = ( ax +by )2 thì ay - bx = 0
\(\left(a^2+b^2\right)\left(x^2+y^2\right)=\left(ax+by\right)^2\)
\(\Leftrightarrow\) \(\dfrac{a}{x}=\dfrac{b}{y}\)
\(\Leftrightarrow ay=bx\)
\(\Leftrightarrow ay-bx=0\)
( Bất đẳng thức Bu - nhi - a - cốp - xki )
Đúng 0
Bình luận (0)
Nếu x + y = - 2 và a - b = -1, sau đó tìm bx + by - ax - ay = ?
\(a-b=-1\Rightarrow b-a=1\)
\(bx+by-ax-ay\\ =b\left(x+y\right)-a\left(x+y\right)\\ =\left(b-a\right)\left(x+y\right)\\ =1.\left(-2\right)\\ =-2\)
Đúng 2
Bình luận (0)
chứng minh
a) (a2+b2+c2)(x2+y2+z2)-(ax+by+cz)2=(bx-ay)2+(cy-bz)2+(az-cx)2
b) (a2+b2)(x2+y2)-(ax+by+cz)2=(ax-by)2+(bx+ay)2
c) nếu (x-y)2+(y-z)2+(z-x)2=(y+z-2x)2+(z+x-2y)2+(x+y-2z)2 thì x=y=z



