cho đường tròn (O1;R1) tiếp xúc ngoài với đườg tròn (O2;R2) vẽ đường thẳng AB là tiếp tuyến chung ngoài của 2 đường tròn (O1)và (O2) vẽ đường tròn (O;R) tiếp xúc ngoài với cả 2 đường tròn (O1);(O2)
cmr :1/R +1/R1+ 1/R2
Cho hình vẽ bên có hai đường tròn (O; 3cm) và ( O 1 ; 3cm). Điểm O 1 nằm trên đường tròn tâm O.
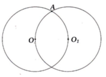
a) Vẽ đường tròn tâm A, bán kính 3cm.
b) Vì sao đường tròn (A; 3cm) đi qua O và O 1 ?
a) HS tự vẽ hình.
b) Đường tròn (A; 3cm) đi qua O và O1 vì OA = O 1 A = 3 cm.
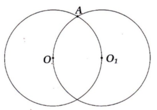
Cho hình vẽ bên có hai đường tròn (O; 3cm) và ( O 1 ; 3cm). Điểm O 1 nằm trên đường tròn tâm O.
a) Vẽ đường tròn tâm A, bán kính 3cm.
b) Vì sao đường tròn (A; 3cm) đi qua O và O 1 ?
a) HS tự vẽ hình.
b) Đường tròn (A; 3cm) đi qua O và O 1 vì O A = O 1 A = 3 c m .
Cho H,K là giao điểm của hai đường tròn tâm O1 và O2.Đường thẳng O1H cắt đường tròn O1 tại A và đường tròn tâm O2 tại B.Đường thẳng O2H cắt đường tròn tâm O1 tại C và đường tròn tâm O2 tại D.Chứng minh:
a, Ba đường thẳng AC,BD,HK đồng quy tại một điểm
b, BH.BA=CH.CD
Bài 1: Cho đường tròn (O1) tiếp xúc trong với đường tròn (O) tại A . Đường kính AB của đường tròn (O) cắt đường tròn (O1) tại điểm thứ hai C khác A . Từ B vẽ tiếp tuyến BP với đường tròn (O1) cắt đường tròn (O) tại Q .Chứng minh AP là phân giác của góc QAB.
Mấy bro giúp mình với T^T
Cho tam giác ABC vuông tại a . Vẽ nửa đường tròn O1 đường kính AB. Nửa đường tròn O2 đường kính AC.Một đường thẳng D quay quanh A cắt đường tròn O1 tại D , O2 tại E.
CMR
Trung điểm DE luôn thuộc đường tròn cố định
Xác định vị trí đường tròn DE sao cho SBDEC lớn nhất
Cho hai đường tròn O, O1 tiếp xúc ngoài nhau tại A. Trên đường tròn O lấy hai điểm phân biệt B, C khác A. Các đường thẳng BA, CA cắt đường tròn O1 lần lượt tại P,Q. cm PQ song song BC
Cho nửa đường tròn (O) đường kính AB. Lấy M là điểm tuỳ ý trên nửa đường tròn (M khác A và B). Kẻ MH vuông góc với AB (H ∈ AB). Trên cùng nửa mặt phang bờ AB chứa nửa đường tròn (O) vẽ hai nửa đường tròn tâm O 1 , đường kính AH và tâm O 2 , đường kính BH. Đoạn MA và MB cắt hai nửa đường tròn ( O 1 ) và ( O 2 ) lần lượt tại P và Q. Chứng minh:
a, MH = PQ
b, Các tam giác MPQ và MBA đồng dạng
c, PQ là tiếp tuyến chung của hai đường tròn ( O 1 ) và ( O 2 )
a, MPHQ là hình chữ nhật => MH = PQ
b, Sử dụng hệ thức lượng trong tam giác vuông chứng minh được MP.MA = MQ.MB => ∆MPQ: ∆MBA
c, P M H ^ = M B H ^ => P Q H ^ = O 2 Q B ^ => PQ là tiếp tuyến của O 2
Tương tự PQ cũng là tiếp tuyến ( O 1 )
BÀI 10.Hãy vẽ hai đường trònC1(O1,R1)vàC1(O2,R2)sao cho hai đường tròn nàycắt nhau tại hai điểm phân biệtA,Btrong hai trường hợp:
1.O1,O2khác phía đường thẳngAB;
2.O1,O2cùng phía đường thẳngAB. mong mn giups mik và vẽ hình với ạ
Cho hai đường tròn ( O1 ) và ( O2 ) ngoài nhau. Gọi AB là một tiếp tuyến chung ngoài và CD là một tiếp tuyến chung trong của hai đường tròn ( A, C ϵ ( O1 ) ; ( B, D ϵ ( O2 ). Chứng minh AC, BD, O1O2 đồng quy
Cho hai đường tròn (O1;R1) và (O2;R2) thỏa mãnO1O22=R12=R22.Khẳng định nào sau đây đúng?
A.Hai đường tròn đã cho tiếp xúc ngoài
B.Hai đường tròn đã cho có đúng hai điểm chung
C.Hai đường tròn đã cho không có điểm chung
D.Hai đường tròn đã cho tiếp xúc trong