Làm câu 2 thôi ạ

Làm giúp em câu 1 , câu 2 thôi ạ !!
1 The gymnast won a total of ten medals at 3 Olympic Games
2 The principal invited a sports star to give a talk at my school yesterday
 làm giúp e câu 2 thôi ạ
làm giúp e câu 2 thôi ạ
Mỗi bài MNG CHỈ cần làm 1-2 câu thôi ạ, để mình dựa theo đó rồi làm tiếp ạ 
Dạ chỉ cần làm câu d bài 2 thôi ạ
\(\sqrt{9x+9}-2\sqrt{\dfrac{x+1}{4}}=4\left(đk:x\ge-1\right)\)
\(\Leftrightarrow3\sqrt{x+1}-\sqrt{x+1}=4\)
\(\Leftrightarrow2\sqrt{x+1}=4\)
\(\Leftrightarrow\sqrt{x+1}=2\Leftrightarrow x+1=4\Leftrightarrow x=3\left(tm\right)\)
Dạ chỉ cần làm bài 2 câu e thôi ạ
Bài 2:
e) \(\sqrt{4x-8}-12\sqrt{\dfrac{x-2}{9}}=\sqrt{x-2}-12\left(đk:x\ge2\right)\)
\(\Leftrightarrow\sqrt{4}.\sqrt{x-2}-12.\sqrt{\dfrac{1}{9}}.\sqrt{x-2}=\sqrt{x-2}-12\)
\(\Leftrightarrow2\sqrt{x-2}-4\sqrt{x-2}=\sqrt{x-2}-12\)
\(\Leftrightarrow3\sqrt{x-2}=12\)
\(\Leftrightarrow\sqrt{x-2}=4\)
\(\Leftrightarrow x-2=16\Leftrightarrow x=18\left(tm\right)\)
d) \(\sqrt{9x+9}-2\sqrt{\dfrac{x+1}{4}}=4\left(đk:x\ge-1\right)\)
\(\Leftrightarrow\sqrt{9}.\sqrt{x+1}-2.\sqrt{\dfrac{1}{4}}.\sqrt{x+1}=4\)
\(\Leftrightarrow3\sqrt{x+1}-\sqrt{x+1}=4\)
\(\Leftrightarrow2\sqrt{x+1}=4\Leftrightarrow\sqrt{x+1}=2\)
\(\Leftrightarrow x+1=4\Leftrightarrow x=3\)
Bài 2:
e) \(\sqrt{4x-8}-12.\sqrt{\dfrac{x-2}{9}}=\sqrt{x-2}-12\Rightarrow\sqrt{4}.\sqrt{x-2}-12.\sqrt{\dfrac{1}{9}}.\sqrt{x-2}=\sqrt{x-2}-12\Rightarrow2\sqrt{x-2}-4.\sqrt{x-2}=\sqrt{x-2}-12\Rightarrow3.\sqrt{x-2}=12\Rightarrow\sqrt{x-2}=4\Rightarrow x-2=16\Rightarrow x=18\left(tm\right)\)
Câu d thôi ạ, câu a, b, c làm rồi ạ
Gấp ạ!!! Làm câu c thôi ạ
c: Ta có: AM//BC
AE⊥BC
Do đó:AM⊥AE
Suy ra: \(\widehat{AME}+\widehat{AEM}=90^0\)
hay \(\widehat{AME}+\widehat{BAD}=90^0\)
GIÚp em làm 1 trong 2 câu thôi ạ, em cảm ơn
a: \(268_{10}=10C_{16}\)
b: \(12C_{16}=\text{100101100}_2\)
câu a thôi ạ, câu b làm rồi
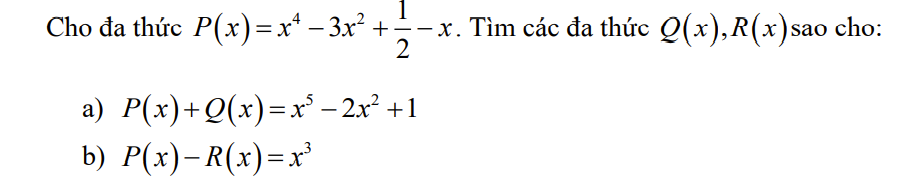
`a)P(x)+Q(x)=x^5-2x^2+1`
`=>Q(x)=x^5-2x^2+1-P(x)`
`=>Q(x)=x^5-2x^2+1-x^4+3x^2-1/2+x`
`=>Q(x)=x^5-x^4+x^2+x+1/2`
______________________________________________
`b)P(x)-R(x)=x^3`
`=>R(x)=P(x)-x^3`
`=>R(x)=x^4-3x^2+1/2-x-x^3`
`=>R(x)=x^4-x^3-3x^2-x+1/2`
Ta có:
\(P\left(x\right)+Q\left(x\right)=x^5-2x^2+1\)
\(\Rightarrow Q\left(x\right)=P\left(x\right)-\left(x^5-2x^2+1\right)\)
\(=x^4-3x^2+\dfrac{1}{2}-x-x^5+2x^2-1\)
\(=-x^5+x^4-x^2-x-\dfrac{1}{2}\)
Vậy \(Q\left(x\right)=-5^2+x^4-x^2-x-\dfrac{1}{2}\)
a) <=> Q(x) = (x5 - 2x2 + 1) - P(x)
= (x5 - 2x2 + 1) - (x4 - 3x2 + 1/2 - x)
= x5 - 2x2 + 1 - x4 + 3x2 + x - 1/2
= x5 - x4 + x2 + x + 1/2
Vậy Q(x) = x5 - x4 + x2 + x + 1/2