cho a/b = c/d chứng minh rằng 7a2+3ab /11a2- 8b2=7c2+3cd / 11c2-8d2
NN
Những câu hỏi liên quan
Chứng minh rằng: nếu
a
b
c
d
thì
a
)
5
a
+
3
b
5
a
−
3
b
5
c
+
3
d
5
c
−
3
d...
Đọc tiếp
Chứng minh rằng: nếu a b = c d thì
a ) 5 a + 3 b 5 a − 3 b = 5 c + 3 d 5 c − 3 d
b ) 7 a 2 + 3 a b 11 a 2 − 8 b 2 = 7 c 2 + 3 c d 11 c 2 − 8 d 2
Cho a/b = c/d với a, b, c, d > 0. Chứng minh rằng\(\dfrac{7a^2+3ab}{11a^2-8b^2}=\dfrac{7c^2+3cd}{11c^2-8d^2}\)
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
\(\dfrac{7a^2+3ab}{11a^2-8b^2}=\dfrac{7b^2k^2+3b^2k}{11b^2k^2-8b^2}=\dfrac{b^2\left(7k^2+3k\right)}{b^2\left(11k^2-8\right)}=\dfrac{7k^2+3k}{11k^2-8}\left(1\right)\)
\(\dfrac{7c^2+3cd}{11c^2-8d^2}=\dfrac{7d^2k^2+3d^2k}{11d^2k^2-8d^2}=\dfrac{d^2\left(7k^2+3k\right)}{d^2\left(11k^2-8\right)}=\dfrac{7k^2+3k}{11k^2-8}\left(2\right)\)
\(\left(1\right)\left(2\right)\RightarrowĐpcm\)
Đúng 1
Bình luận (0)
cho \(\dfrac{a}{b}=\dfrac{c}{d}\) Chứng minh rằng
\(\dfrac{7a^2+3ab}{11a^2+8b^2}=\dfrac{7c^2+3cd}{11c^2-8d^2}\)
1) Cho dfrac{a}{b}dfrac{c}{d} . Chứng minh rằng dfrac{2a^2-3ab+5b^2}{2a^2+3ab}dfrac{2c^2-3cd+5d^2}{2c^2+3cd}
2) Cho dfrac{a}{c}dfrac{c}{b}. Chứng minh rằng dfrac{b^2-c^2}{a^2+c^2}dfrac{b-a}{a}
3) Cho dfrac{a}{b}dfrac{c}{d}.Chứng minh rằngdfrac{3a^6+c^6}{3b^6+d^6}dfrac{left(a+cright)^6}{left(b+dright)^6}
Đọc tiếp
1) Cho \(\dfrac{a}{b}=\dfrac{c}{d}\) . Chứng minh rằng \(\dfrac{2a^2-3ab+5b^2}{2a^2+3ab}=\dfrac{2c^2-3cd+5d^2}{2c^2+3cd}\)
2) Cho \(\dfrac{a}{c}=\dfrac{c}{b}\). Chứng minh rằng \(\dfrac{b^2-c^2}{a^2+c^2}=\dfrac{b-a}{a}\)
3) Cho \(\dfrac{a}{b}=\dfrac{c}{d}\).Chứng minh rằng\(\dfrac{3a^6+c^6}{3b^6+d^6}=\dfrac{\left(a+c\right)^6}{\left(b+d\right)^6}\)
Bài 1:
$\frac{a}{b}=\frac{c}{d}=t\Rightarrow a=bt; c=dt$. Khi đó:
\(\frac{2a^2-3ab+5b^2}{2a^2+3ab}=\frac{2(bt)^2-3.bt.b+5b^2}{2(bt)^2+3bt.b}=\frac{b^2(2t^2-3t+5)}{b^2(2t^2+3t)}\)
$=\frac{2t^2-3t+5}{2t^2+3t}(1)$
\(\frac{2c^2-3cd+5d^2}{2c^2+3cd}=\frac{2(dt)^2-3.dt.d+5d^2}{2(dt)^2+3dt.d}=\frac{d^2(2t^2-3t+5)}{d^2(2t^2+3t)}=\frac{2t^2-3t+5}{2t^2+3t}(2)\)
Từ $(1);(2)$ suy ra đpcm.
Bài 2:
Từ $\frac{a}{c}=\frac{c}{b}\Rightarrow c^2=ab$. Khi đó:
$\frac{b^2-c^2}{a^2+c^2}=\frac{b^2-ab}{a^2+ab}=\frac{b(b-a)}{a(a+b)}$ (đpcm)
Bài 3:
Đặt $\frac{a}{b}=\frac{c}{d}=t\Rightarrow a=bt; c=dt$
Khi đó:
$\frac{3a^6+c^6}{3b^6+d^6}=\frac{3(bt)^6+(dt)^6}{3b^6+d^6}=\frac{t^6(3b^6+d^6)}{3b^6+d^6}=t^6(*)$
Và:
$\frac{(a+c)^6}{(b+d)^6}=(\frac{bt+dt}{b+d})^6=t^6(**)$
Từ $(*); (**)\Rightarrow $ đpcm.
Cho \(\frac{a}{b}=\frac{c}{d}\)
Chứng minh rằng : (a+2015c)(b+d)=(a+c)(b+2015d)
Cho \(\frac{a}{b}=\frac{c}{d}\)
Chứng minh rằng: \(\frac{2a^2-3ab+5b^2}{2b^2+3ab}=\frac{2c^2-3cd+5d^2}{2d^2+3cd}\)
đg cần gấp nka m.ng záng zúp mk
Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk,c=dk\)
\(\frac{2a^2-3ab+5b^2}{2b^2+3ab}=\frac{2.\left(bk\right)^2-3.bk.b+5.b^2}{2b^2+3.bk.b}\)=\(\frac{2.b^2.k^2-3.k.b^2+5.b^2}{2.b^2+3.b^2.k}=\frac{b^2\left(2.k^2-3.k+5\right)}{b^2\left(2+3.k\right)}=\frac{2.k^2-3.k+5}{2+3.k}\)
\(\frac{2c^2-3cd+5d^2}{2d^2+3cd}=\frac{2.\left(dk\right)^2-3.dk.d+5.d^2}{2.d^2+3.dk.d}\)\(=\frac{2.d^2.k^2-3.d^2.k+5.d^2}{2.d^2+3.d.k.d}\)=\(\frac{d^2\left(2.k^2-3.k+5\right)}{d^2\left(2+3.k\right)}=\frac{2.k^2-3.k+5}{2+3.k}\)
=> bằng nhau
Đúng 0
Bình luận (0)
Bằng nhau pạn nhé. Mjk ko tjện giảj nha pạn tự làm nha.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tỉ lệ thức: \(\frac{a}{b}=\frac{c}{d}\). Chứng minh: \(\frac{2a^2-3ab+5b^2}{2b^2+3ab}=\frac{2c^2-3cd+5d^2}{2d^2+3cd}\)
Bạn tham Khảo: https://hoc24.vn/hoi-dap/question/230602.html
Cho tỉ lệ thức\(\dfrac{a}{b}\)=\(\dfrac{c}{d}\). Chứng minh rằng ta có tỉ lệ sau: \(\dfrac{7a^2+3ab}{11a^2-8b^2}\)=\(\dfrac{7c^2+3cd}{11c^2-8d^2}\)
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Rightarrow a=bk;c=dk\)
Ta có: \(VT=\dfrac{7a^2+3ab}{11a^2-8b^2}=\dfrac{7bk^2+3bkb}{11bk^2-8b^2}=\dfrac{7b^2k^2+3b^2k}{11b^2k^2-8b^2}=\dfrac{b^2\left(7k^2+3k\right)}{b^2\left(11k^2-8\right)}=\dfrac{7k^2+3k}{11k^2-8}\)
\(VP=\dfrac{7c^2+3cd}{11c^2-8d^2}=\dfrac{7dk^2+3dkd}{11dk^2-8d^2}=\dfrac{7d^2k^2+3d^2k}{11d^2k^2-8d^2}=\dfrac{d^2\left(7k^2+3k\right)}{d^2\left(11k^2-8\right)}=\dfrac{7k^2+3k}{11k^2-8}\)
\(\Rightarrow VT=VP\)
Vậy \(\dfrac{7a^2+3ab}{11a^2-8b^2}=\dfrac{7c^2+3cd}{11c^2-8d^2}\left(đpcm\right)\)
Đúng 1
Bình luận (0)
* VT là vế trái // VP là vế phải *
\(#tutuuu..\)
Đúng 0
Bình luận (0)
Cho \(\dfrac{a}{b}=\dfrac{c}{d}\)với ( ab > 0 ).Chứng minh;
\(\dfrac{2a^2-3ab+5b^2}{2b^2+3ab}=\dfrac{2c^2-3cd+5d^2}{2d^2+3cd}\)
đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Thay a và c vào VP và VT sẽ bằng nhau
Đúng 0
Bình luận (0)
Cho tỉ lệ thức: \(\dfrac{a}{b}=\dfrac{c}{d}\). Chứng minh:
\(\dfrac{2a^2-3ab+5b^2}{2b^2+3ab}=\dfrac{2c^2-3cd+5d^2}{2d^2+3cd}\)
Đặt: \(\dfrac{a}{b}=\dfrac{c}{d}=k\\ \Rightarrow a=bk;c=dk\)
Ta có:
\(\dfrac{2a^2-3ab+5b^2}{2b^2+3ab}=\dfrac{2\left(bk\right)^2-2bkb+5b^2}{2b^2+3bkb}=\dfrac{2b^2k^2-2b^2k+5b^2}{2b^2+3b^2k}=\dfrac{b^2\left(2k^2-3k+5\right)}{b^2\left(2+3k\right)}=\dfrac{2k^2-3k+5}{2+3k}\left(1\right)\)
\(\dfrac{2c^2-3cd+5d^2}{2d^2+3cd}=\dfrac{2\left(dk\right)^2-3dkd+5d^2}{2d^2+3dkd}=\dfrac{2d^2k^2-3d^2k+5d^2}{2d^2+3d^2k}=\dfrac{d^2\left(2k^2-3k+5\right)}{d^2\left(2+3k\right)}=\dfrac{2k^2-3k+5}{2+3k}\left(2\right)\)
Từ (1) và (2) suy ra:
\(\dfrac{2a^2-3ab+5b^2}{2b^2+3ab}=\dfrac{2c^2-3cd+5d^2}{2d^2+3cd}\)
Đúng 0
Bình luận (0)
Giải:
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{2a^2-3ab+5b^2}{2b^2+3ab}=\dfrac{2b^2k^2-3b^2k+5d^2}{2b^2+3b^2k}\)
\(=\dfrac{b^2k\left(2k-3k+5\right)}{b^2\left(2+3k\right)}=\dfrac{k\left(2k-3+5\right)}{2+3k}\) (1)
\(\dfrac{2c^2-3cd+5d^2}{2d^2+3cd}=\dfrac{2d^2k^2-3d^2k+5d^2}{2d^2+3d^2k}\)
\(=\dfrac{d^2k\left(2k-3+5\right)}{d^2\left(2+3k\right)}=\dfrac{k\left(2k-3+5\right)}{2+3k}\) (2)
Từ (1), (2) \(\Rightarrow\dfrac{2a^2-3ab+5b^2}{2b^2+3ab}=\dfrac{2c^2-3cd+5d^2}{2d^2+3cd}\left(đpcm\right)\)
Đúng 0
Bình luận (4)
Cho a/b=c/d Chứng minh rằng 7a2+5ac/ 7a2 - 5ac = 7b2+5bd / 7b2- 5bd


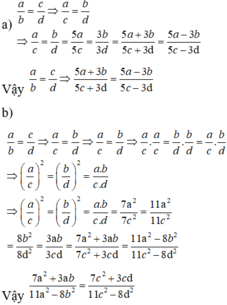





 Ai help me vs
Ai help me vs