Các hằng đẳng thức nâng cao
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
MP
Những câu hỏi liên quan
Các hằng đẳng thức nâng cao
giúp mình với !!!
Bọn óc chó, chúng mày đang coppy bài lớp 8 đấy :))
Đúng 0
Bình luận (0)
1. ( a + b + c )3 = a3 + b3 +c3 + 3( a + b )( b + c)( c + a )2. a3 + b3 + c3 – 3abc = ( a + b + c)(a2 + b2 + c2 – ab – bc – ca )3. ( a – b – c )2 = a2 + b2 + c2 – 2ab + 2bc – 2ca4. ( a + b + c )2 = a2 + b2 + c2 + 2ab + 2bc + 2ca5. ( a + b – c )2 = a2 + b2 + c2 + 2ab – 2bc – 2 ca
Đúng 0
Bình luận (0)
1. ( a + b + c )3 = a3 + b3 +c3 + 3( a + b )( b + c)( c + a )
2. a3 + b3 + c3 – 3abc = ( a + b + c)(a2 + b2 + c2 – ab – bc – ca )
3. ( a – b – c )2 = a2 + b2 + c2 – 2ab + 2bc – 2ca
4. ( a + b + c )2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
5. ( a + b – c )2 = a2 + b2 + c2 + 2ab – 2bc – 2 ca.
Đúng 0
Bình luận (0)
Có ai biết những hằng đẳng thức nâng cao lớp 9 ko?? Hay dùng trong các kì thi í =)))
Các bạn giúp mik sưu tầm mấy bài toàn nâng cao về nhân đa thức với da thức, đơn thức với đa thức, các hằng đẳng thức đáng nhớ... Lớp 8 nha
AI BIẾT NHIỀU BÀI MIK TICK CHO NHA
các bạn ơi,cho mình các bất đẳng thức nâng cao đi
OK bạn
Ví dụ 1: Cho a, b,c là các số không âm chứng minh rằng
(a+b)(b+c)(c+a)≥≥8abc
Cho các số thực dương a,b,c thỏa mãn điều kiện a + b + c = 3 . Tìm giá trị nhỏ nhất của \(A=4a^2+6b^2+3c^2\)
Đây nhé
HT
I. Một số ví dụ:
Ví dụ 1: Cho a, b,c là các số không âm chứng minh rằng
(a+b)(b+c)(c+a)≥≥8abc
Giải:
Dùng bất đẳng thức phụ:(x+y)2≥4xy(x+y)2≥4xy
Ta có (a+b)2≥4ab(a+b)2≥4ab ;(c+b)2≥4cb(c+b)2≥4cb;(a+c)2≥4ac(a+c)2≥4ac
⇒(a+b)2(b+c)2(a+c)2≥64(abc)2⇒(a+b)2(b+c)2(a+c)2≥64(abc)2
do đó (a+b)(b+c)(c+a)≥≥8abc
Dấu “=” xảy ra khi a = b = c
Xem thêm câu trả lời
hằng đẳng thức bậc cao ?
(6) (a+b+c)3=a3+b3+c3+3(a+b)(b+c)(c+a)(a+b+c)3=a3+b3+c3+3(a+b)(b+c)(c+a)
(7) a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−bc−ac)a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−bc−ac)
(8) (a−b)3+(b−c)3+(c−a)3=3(a−b)(b−c)(c−a)(a−b)3+(b−c)3+(c−a)3=3(a−b)(b−c)(c−a)
(9) (a+b)(b+c)(c+a)−8abc=a(b−c)2+b(c−a)2+c(a−b)2(a+b)(b+c)(c+a)−8abc=a(b−c)2+b(c−a)2+c(a−b)2
(10) (a+b)(b+c)(c+a)=(a+b+c)(ab+bc+ca)−abc(a+b)(b+c)(c+a)=(a+b+c)(ab+bc+ca)−abc
(11) ab2+bc2+ca2−a2b−b2c−c2a=(a−b)3+(b−c)3+(c−a)33ab2+bc2+ca2−a2b−b2c−c2a=(a−b)3+(b−c)3+(c−a)33
(12)ab3+bc3+ca3−a3b−b3c−c3a=(a+b+c)[(a−b)3+(b−c)3+(c−a)3]3ab3+bc3+ca3−a3b−b3c−c3a=(a+b+c)[(a−b)3+(b−c)3+(c−a)3]3
(13) an−bn=(a−b)(an−1+an−2b+an−3b2+...+a2bn−3+abn−2+bn−1)an−bn=(a−b)(an−1+an−2b+an−3b2+...+a2bn−3+abn−2+bn−1)
(14) Với n lẻ:
an+bn=(a+b)(an−1−an−2b+an−3b2−...+a2bn−3−abn−2+bn−1)an+bn=(a+b)(an−1−an−2b+an−3b2−...+a2bn−3−abn−2+bn−1)
(15) Nhị thức Newton:
(a+b)n=an+n!(n−1)!1!an−1b+n!(n−2)!2!an−2b2+...+n!(n−k)!k!an−kbk+...+n!2!(n−2)!a2bn−2+n)!1!(n−1)!abn−1+bn
Đúng 0
Bình luận (0)
RÚT GỌN CÁC BIỂU THỨC SAU:
Gợi ý: Dùng hằng đẳng thức để rút gọn nhanh hơn (nhưng cũng phải biến đổi rõ ràng ra rồi mới ra hằng đẳng thức chứ ko đc làm nhanh bằng cách ghi hằng đẳng thức ngay!)
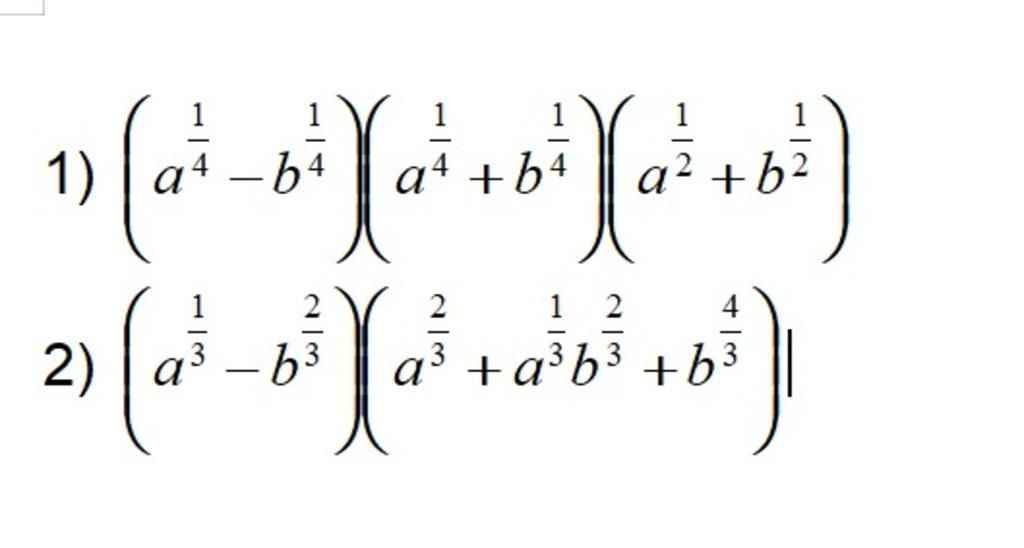
`1)(a^[1/4]-b^[1/4])(a^[1/4]+b^[1/4])(a^[1/2]+b^[1/2])`
`=[(a^[1/4])^2-(b^[1/4])^2](a^[1/2]+b^[1/2])`
`=(a^[1/2]-b^[1/2])(a^[1/2]+b^[1/2])`
`=a-b`
`2)(a^[1/3]-b^[2/3])(a^[2/3]+a^[1/3]b^[2/3]+b^[4/3])`
`=(a^[1/3]-b^[2/3])[(a^[1/3])^2+a^[1/3]b^[2/3]+(b^[2/3])^2]`
`=(a^[1/3])^3-(b^[2/3])^3`
`=a-b^2`
Đúng 4
Bình luận (0)
bài mẫu (2x-3)^2-10.(2x-3)+25
=(2x-3)^2_10.(2x-3)+25
=[(2x-3)-5]^2
=(2x-8)^2
ÁP DỤNG NÂNG CAO HƠN
(2x-5)^2+2(2x-5)(3x+1)+(3x+1)^2
Nâng cao lên có một chút thôi nhưng mà tui ko biết làm ai giúp tôi với :(( biến nó thành hằng đẳng thức giống cách trên
giúp tui với help me làm ơn
(2x-5)2+2(2x-5)(3x+1)+(3x+1)2
=(2x-5)[(2x-5)+2(3x+1)]+(3x+1)2
=(2x-5)[8x-3]+(3x+1)2
=16x2-46x+15+9x2+6x+1
=25x2-40x+16
=(5x)2-2*5x*4+42
=(5x-4)2
Đúng 0
Bình luận (0)
phần nâng cao chính là một hằng đẳng thức hoàn chỉnh (a+b)2. trong đó 2x-5 là a và 3x+1 là b
Đúng 0
Bình luận (0)
rất xin lỗi vì bài mẫu tôi ghi thiếu tôi đã sửa lại nhờ mọi người giúp tôi cách giải ngắn gọn giống bài mẩu cách của bạn Thắng Nguyễn dc nhưng quá dài xin ai hãy giải cho tôi giống cách của bài mẫu (2x-3)^2-10.(2x-3)+25
=(2x-3)^2-2.5.(2x-3)+5^2
=[(2x-3)-5]^2
=(2x-8)^2
ÁP DỤNG NÂNG CAO HƠN
(2x-5)^2+2(2x-5)(3x+1)+(3x+1)^2
Nâng cao lên có một chút thôi nhưng mà tui ko biết làm ai giúp tôi với :(( biến nó thành hằng đẳng thức giống cách trên
giúp tui với help me làm ơn
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm giá trị lớn nhất của biểu thức \(P=\dfrac{x+3}{\sqrt{x^2+1}}\) với \(x\in\left(0;+\infty\right)\).
Note: Không sử dụng đạo hàm và các bất đẳng thức nâng cao.
\(\left(x+3\right)^2=x^2+6x+9\le x^2+\left(9x^2+1\right)+9=10\left(x^2+1\right)\)
Suy ra: \(P=\dfrac{x+3}{\sqrt{x^2+1}}\le\sqrt{10}\)
Vậy \(MaxP=\sqrt{10}\) (khi \(x=\dfrac{1}{3}\))
Đúng 0
Bình luận (2)
Từ định nghĩa của sinα, cosα. Hãy chứng minh hằng đẳng thức đầu tiên, từ đó suy ra các hằng đẳng thức còn lại.
cosα = OH¯; sinα = OK¯
Do tam giác OMK vuông tại K nên:
sin2 α + cos2 α = OK¯2 + OH¯2 = OK2 + MK2 = OM2 = 1.
Vậy sin2 α + cos2 α = 1.
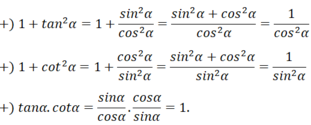
Đúng 0
Bình luận (0)



