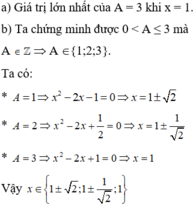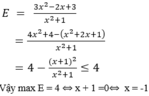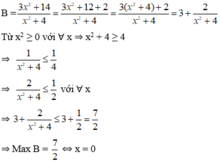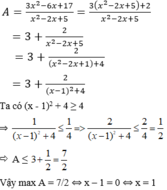\(C=-3x^2+12x-7=-3\left(x^2-4x+4\right)+12-7=-3\left(x-2\right)^2+5\le5\)

\(maxC=5\Leftrightarrow x=2\)

\(C=-3\left(x^2+4x+4\right)+5=-3\left(x+2\right)^2+5\le5\)

Dấu \("="\Leftrightarrow x=-2\)

a.  ta có (2x-5)² >= 0 với mọi x thuộc R

vậy 5 -(2x-5)² <= 5

dấu = xảy ra khi (2x-5)²=0

                     vậy 2x-5=0

                           2x =5

                            x= 5/2=2,5

Vậy để B lớn nhất thì x=2,5

b. ta có | 2x-4| >= 0 với mọi x thuộc R 

             | 2x-6| >= 0 với mọi x thuộc R

vậy | 2x-4 |- |2x-6| >= 0 

dấu = xảy ra khi |2x-4|          và            |2x-6|              đều bằng 0

                   => 2x-4=0                      => 2x - 6=0

                       2x =4                              2x =6

                        x=4/2=2                          x= 6/2=3

Câu b mình viết nhầm dấu \(\ge\)đáng lẽ đúng phải là \(\le\)

a)

\(A=x^2+y^2-x+6y+10.\)

\(=\left(x^2-x+\frac{1}{4}\right)+\left(y^2+6y+9\right)+\frac{3}{4}\)

\(=\left(x-\frac{1}{2}\right)^2+\left(y+3\right)^2+\frac{3}{4}\ge\frac{3}{4}\)

Vậy \(MinA=\frac{3}{4}\Leftrightarrow\hept{\begin{cases}\left(x-\frac{1}{2}\right)^2=0\\\left(y+3\right)^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x-\frac{1}{2}=0\\y+3=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{1}{2}\\y=-3\end{cases}}}\)

b)

\(B=2x-2x^2-5\)

\(=-2\left(x^2-x+\frac{1}{4}\right)+2.\frac{1}{4}-5\)

\(=-2\left(x-\frac{1}{2}\right)^2-\frac{9}{2}\ge-\frac{9}{2}\)

Vậy \(MaxB=-\frac{9}{2}\Leftrightarrow\left(x-\frac{1}{2}\right)^2=0\Leftrightarrow x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}\)

a) x² + y² - x + 6y + 10 = (x² - x + 1/4) + (y² + 6y + 9) + 3/4

=(x - 1/2)² + (y + 3)² + 3/4 \(\ge\)3/4

Dấu "=" xảy ra <=> (x - 1/2)² = 0 và (y + 3)² = 0   <=> x = 1/2 ; y = -3

Vậy GTNN của bt đã cho là 3/4 khi x = 1/2 và y = -3

b) A = 2x - 2x² - 5

<=> 2A = 2(2x -  2x² - 5)

<=> 2A = -4x² + 4x - 5

<=> 2A = -(4x² - 4x + 1) - 4

<=> 2A = -(2x - 1)² - 4\(\le\)-4

<=> A \(\le\)-2

Dấu "=" xảy ra <=>: (2x - 1)² = 0   <=> x = 1/2

Vậy GT LN của bt đã cho là -2 khi và chỉ khi x = 1/2

\(E=-4x^2+x+1\)

\(\Rightarrow E=-4\left(x^2-\dfrac{x}{4}\right)+1\)

\(\Rightarrow E=-4\left(x^2-\dfrac{x}{4}+\dfrac{1}{64}\right)+1+\dfrac{1}{16}\)

\(\Rightarrow E=-4\left(x-\dfrac{1}{8}\right)^2+\dfrac{17}{16}\)

 mà \(-4\left(x-\dfrac{1}{8}\right)^2\le0,\forall x\)

\(\Rightarrow E=-4\left(x-\dfrac{1}{8}\right)^2+\dfrac{17}{16}\le\dfrac{17}{16}\)

\(\Rightarrow GTLN\left(E\right)=\dfrac{17}{16}\left(tạix=\dfrac{1}{8}\right)\)

\(F=5x-3x^2+6\)

\(\Rightarrow F=-3\left(x^2-\dfrac{5x}{3}\right)+6\)

\(\Rightarrow F=-3\left(x^2-\dfrac{5x}{3}+\dfrac{25}{36}\right)+6+\dfrac{25}{12}\)

\(\Rightarrow F=-3\left(x-\dfrac{5}{6}\right)^2+\dfrac{97}{12}\)

mà \(-3\left(x-\dfrac{5}{6}\right)^2\le0,\forall x\)

\(\Rightarrow F=-3\left(x-\dfrac{5}{6}\right)^2+\dfrac{97}{12}\le\dfrac{97}{12}\)

\(\Rightarrow GTLN\left(F\right)=\dfrac{97}{12}\left(tạix=\dfrac{5}{6}\right)\)

E=?

F=?

a) Ta có: \(\left(x-2\right)^2\ge0\forall x\)

nên Dấu '=' xảy ra khi x-2=0

hay x=2

Vậy: Gtnn của biểu thức \(\left(x-2\right)^2\) là 0 khi x=2