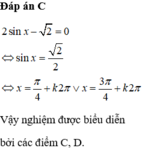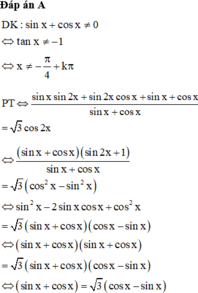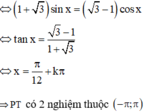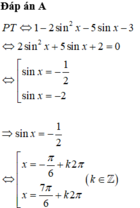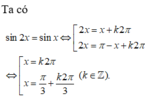nghiệm của phương trình lượng giác \(\sin^2x-2\sin x=0\)là
NL
Những câu hỏi liên quan
Nghiệm của phương trình
2
.
sin
x
-
2
0
được biểu diễn trên đường tròn lượng giác ở hình bên là những điểm nào? A. Điểm C, điểm E B. Điểm F, điểm E C. Điểm C, điểm D D. Điểm C, điểm F
Đọc tiếp
Nghiệm của phương trình 2 . sin x - 2 = 0 được biểu diễn trên đường tròn lượng giác ở hình bên là những điểm nào?
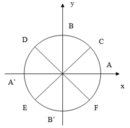
A. Điểm C, điểm E
B. Điểm F, điểm E
C. Điểm C, điểm D
D. Điểm C, điểm F
Số nghiệm của phương trình
sin
x
.
sin
2
x
+
2
.
sin
x
.
cos
2...
Đọc tiếp
Số nghiệm của phương trình sin x . sin 2 x + 2 . sin x . cos 2 x + sin x + cos x sin x + cos x = 3 . cos 2 x trong khoảng - π , π là:
A. 2
B. 4
C. 3
D. 5
Giải phương trình lượng giác: \(sin^23x.cos2x+sin^2x=0\)
\(sin^23x.cos2x+sin^2x=0\)
\(\left(3sinx-4sin^3x\right)^2.cos2x+sin^2x=0\)
\(sin^2x\left[\left(3-4sin^2x\right)^2.cos2x+1\right]=0\)
\(sin^2x\left[\left(1+2cos2x\right)^2.cos2x+1\right]=0\)
\(sin^2x\left(4cos^22x+1\right)\left(cos2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\cos2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\text{π}\\2x=k2\text{π}\end{matrix}\right.\)\(\Leftrightarrow x=k\text{π}\)
Đúng 2
Bình luận (3)
\(sin^23xcos2x+sin^2x=0\rightarrow\dfrac{1-cos6x}{2}.cos2x+\dfrac{1-cos2x}{2}=0\\ \rightarrow cos6xcos2x=1\rightarrow cos8x+cos4x=2\\ \rightarrow cos8x=cos4x=1\rightarrow x=\dfrac{k\pi}{2}\left(k\in Z\right)\)
Đúng 0
Bình luận (0)
Tìm tất cả các nghiệm của phương trình sin x + sin 2x + sin3x = 0 thuộc ( 0 ; π )
A. 3
B. 4
C. 5
D. 6
Nghiệm của phương trình lượng giác sin(x + pi/3) =-1 là
=>x+pi/3=-pi/2+k2pi
=>x=-5/6pi+k2pi
Đúng 0
Bình luận (0)
Nghiệm của phương trình
cos
2
x
+
3
sin
x
-
2
cos
x
0
là
Đọc tiếp
Nghiệm của phương trình cos 2 x + 3 sin x - 2 cos x = 0 là
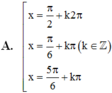
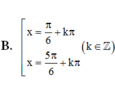
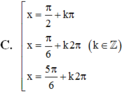
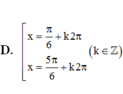
Đáp án D
Tìm điều kiện để phương trình có nghĩa. Sau đó sử dụng công thức 2 cos 2 x = 1 - 2 sin 2 x để đưa phương trình đã cho về phương trình bậc 2 đối với sin x và giải phương trình này để tìm nghiệm. Bước cuối cùng là đối chiếu điều kiện để kết luận nghiệm.
Điều kiện
![]()
Với điều kiện trên phương trình đã cho trở thành
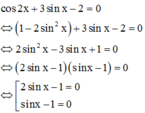
Nếu
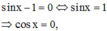
không thỏa mãn điều kiện (1)
Vậy
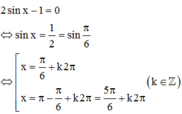
Đúng 0
Bình luận (0)
Nghiệm của phương trình cos 2x – 5. sin x – 3 0 là:
Đọc tiếp
Nghiệm của phương trình cos 2x – 5. sin x – 3 = 0 là:
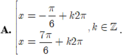
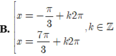
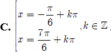
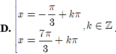
Cho phương trình
cos
x
+
sin
x
1
+
sin
2
x
+
cos
2
x
. Nghiệm của phương trình có dạng
x
1
a
π
+
k
π
.
x
2
±
b
π
+
k
2
π
b
0
Tính tổng a + b A. ...
Đọc tiếp
Cho phương trình cos x + sin x = 1 + sin 2 x + cos 2 x . Nghiệm của phương trình có dạng x 1 = a π + k π . x 2 = ± b π + k 2 π b > 0 Tính tổng a + b
A. 1 12
B. 3
C. 7 π 12
D. π 4
Tập nghiệm của phương trình
sin
2
x
sin
x
là A.
S
k
2
π
;
π
3
+
k
2
π
|
...
Đọc tiếp
Tập nghiệm của phương trình
sin 2 x = sin x là
A. S = k 2 π ; π 3 + k 2 π | k ∈ ℤ
B. S = k 2 π ; π 3 + k 2 π 3 | k ∈ ℤ
C. S = k 2 π ; - π 3 + k 2 π | k ∈ ℤ
D. S = k 2 π ; π + k 2 π | k ∈ ℤ