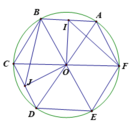
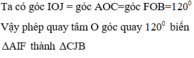cho lục giác đều ABCDEF,M và N là trung điểm CD,DE.Gọi I là giao điểm AM,BN.tính góc OID
ML
Những câu hỏi liên quan
Cho lục giác đều ABCDEF, M và N theo thứ tự là trung điểm của CD, DE. I là giao điểm của AM và BN
a) Tính \(\widehat{AIB}.\)
b) Tính \(\widehat{OID}\)( O là tâm của lục giác đều )
a. Ta thấy \(\Delta ABC=\Delta BCD\left(c-g-c\right)\Rightarrow AC=BD;\widehat{ACB}=\widehat{BDC}\)
\(\Rightarrow\widehat{ACM}=\widehat{BDN}\Rightarrow\Delta AMC=\Delta BND\left(c-g-c\right)\)
\(\Rightarrow\widehat{AMC}=\widehat{BND}\Rightarrow\widehat{AMC}+\widehat{AMD}=\widehat{BND}+\widehat{AMD}=180^o\)
\(\Rightarrow\widehat{NIM}+\widehat{NDM}=180^o\Rightarrow\widehat{AIB}=180^o-120^o=60^o.\)
b. Ta thấy ON vuông góc ED nên ON cũng vuông góc AB. Lại có tam giác ANB cân tại N; NO là đường cao nên nó là phân giác. Vậy \(\widehat{ANO}=\widehat{BNO}\)
Lại có AD là trung trực MN nên \(\widehat{ANO}=\widehat{AMO}\Rightarrow\widehat{BNO}=\widehat{AMO}\Rightarrow\) tứ giác OIMN nội tiếp.
Lại dễ thấy OMDN cũng nội tiếp nên O; I; M ;D; N cùng thuộc đường trong đường kính OD. Vậy \(\widehat{OID}=90^o.\)
(Cô làm theo cách lớp 9)
Đúng 0
Bình luận (0)
em gửi bài qua fb thầy chữa cho nhé, tìm fb của thầy bằng sđt: 0975705122 nhé.
Đúng 0
Bình luận (0)
http://olm.vn/hoi-dap/question/750403.html
Bà Dung làm đê
Đề tui tự chế dok
#Silver bullet
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho lục giác đều ABCDEF, M và N theo thứu tự là trung điểm của CD, DE. Gọi I là giao điểm của AM và BN .Tính góc AIB
Bài 3: Cho lục giác ABCDEF có số đo các góc (tính theo độ) là 1 số nguyên và góc A-góc B=góc B-góc C=góc C-góc D=góc D-góc E=góc E-góc F. Tính giá trị lớn nhất của góc A.
Bài 4: Cho lục giác đều ABCDEF. M, N lần lượt là trung điểm của CD, DE. AM cắt BN tại I.
a) Góc AIB=?
b) Góc OID=? (biết O là tâm của lục giác đều)
Cho lục giác đều ABCDEF; M và N theo thứ tự là trung điểm của các đoạn thẳng CD và DE; K là giao điểm của AM và BN. Chứng minh;
\(a.Sabk=Smknd\)
b. Góc nhọn giữa AM và BN bằng 60 độ.
Cho lục giác đều ABCDEF. Gọi H là giao điểm của AE và FC, gọi K là trung điểm của CD. Chứng minh tam giác BHK đều.
cho lục giác đều abcdef các điểm m, n, p lần lượt là trung điểm các cạnh ab ,cd ,ef . cmr mnp là tam giác đều
Cho lục giác đều ABCDEF nội tiếp đường tròn tâm O, gọi I là trung điểm của AB và J là trung điểm của CD. Hỏi ảnh của tam giác AIF qua phép quay tâm O, góc quay
120
°
là tam giác nào dưới đây? A.
Δ
EJD
B.
Δ
F
J
E
C.
Δ
C
J
B
D.
Δ
OJD
Đọc tiếp
Cho lục giác đều ABCDEF nội tiếp đường tròn tâm O, gọi I là trung điểm của AB và J là trung điểm của CD. Hỏi ảnh của tam giác AIF qua phép quay tâm O, góc quay 120 ° là tam giác nào dưới đây?
A. Δ EJD
B. Δ F J E
C. Δ C J B
D. Δ OJD
Cho lục giác đều ABCDEF. Gọi I và K là trung điểm của các cạnh CD và DE, còn P là giao điểm của AI và BK. Chứng minh rằng SABP=SIDKP
cho lục giác đều ABCDEF. M, N, P lần lượt là trung điểm các cạnh AB, CD, EF.CMR: tam giác MNP đều