phương trình dao dộng của vật có dạng x = 3Asin wt + 4Acos wt. biên độ dao động của vật là/
LA
Những câu hỏi liên quan
Phương trình dao động của vật có dạng x = 3Asin\omegat + 4Acos\omegat. Biên độ dao động của vật là:
Xem chi tiết
\(x=3sin\omega t=3Acos\left(\omega t-\dfrac{\pi}{2}\right)+4Acos\omega t\) => Hai dao động vuông pha.
Biên độ dao động của vật là \(A'=\sqrt{\left(3A\right)^2+\left(4A\right)^2}=5A\)
Đúng 1
Bình luận (0)
Một vật dao động điều hòa có phương trình x Acos(wt + φ). Gọi v là vận tốc của vật khi vật ở li độ x. Biên độ dao động của vật là A.
x
2
+
v
2
ω
2
B. ...
Đọc tiếp
Một vật dao động điều hòa có phương trình x = Acos(wt + φ). Gọi v là vận tốc của vật khi vật ở li độ x. Biên độ dao động của vật là
A. x 2 + v 2 ω 2
B. x + v 2 ω 4
C. x + v 2 ω 4
D. x 2 + v 4 ω 2
Đáp án A
+ Biên độ dao động của vật dao động điều hòa có li độ x, vận tốc v:
x 2 + v 2 ω 2
Đúng 0
Bình luận (0)
Một vật dao động điều hòa có phương trình
x
A
cos
(
w
t
+
φ
)
. Gọi v là vận tốc của vật khi vật ở li độ x. Biên độ dao động của vật là A.
x
2
+
v
2
ω
2
B. ...
Đọc tiếp
Một vật dao động điều hòa có phương trình x = A cos ( w t + φ ) . Gọi v là vận tốc của vật khi vật ở li độ x. Biên độ dao động của vật là
A. x 2 + v 2 ω 2
B. x 2 + v 2 ω 4
C. x + v 2 ω 2
D. x 2 + v 4 ω 2
Một vật thực hiện đồng thời hai dao động điều hoà cùng phương cùng tần số có phương trình: x1 A1sin(wt + j1)cm, x2 A2cos(wt + j2)cm. Thì biên độ của dao động tổng hợp lớn nhất khi A. j2 - j1 (2k+1)p. B. j2 - j1 k2p - p/2. C. j2 - j1 2kp. D. j2 - j1 k2p + p/2.
Đọc tiếp
Một vật thực hiện đồng thời hai dao động điều hoà cùng phương cùng tần số có phương trình: x1 = A1sin(wt + j1)cm, x2 = A2cos(wt + j2)cm. Thì biên độ của dao động tổng hợp lớn nhất khi
A. j2 - j1 = (2k+1)p.
B. j2 - j1 = k2p - p/2.
C. j2 - j1 = 2kp.
D. j2 - j1 = k2p + p/2.
Một vật có khối lượng 1 kg dao động điều hòa. Chọn gốc tọa độ và gốc thế năng tại vị trí cân bằng. Vật có phương trình dao động là x Acos
ω
t
+
φ
và biểu thức thế năng của vật là
W
t
0
,
1
cos
4
πt
+
π...
Đọc tiếp
Một vật có khối lượng 1 kg dao động điều hòa. Chọn gốc tọa độ và gốc thế năng tại vị trí cân bằng. Vật có phương trình dao động là x = Acos ω t + φ và biểu thức thế năng của vật là W t = 0 , 1 cos 4 πt + π 2 + 0 , 1 J (J). Lấy π 2 = 10 . Phương trình dao động của vật là
A. x = 10 cos 2 πt + π 4 c m
B. x = 5 cos 2 πt + π 2 c m
C. x = 10 cos 4 πt + π 4 c m x = 5 cos 2 πt + π 4 c m
D. x = 5 cos 2 πt + π 4 c m
ü Đáp án A
+ Phương trình của thế năng là:
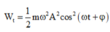
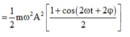
+ Phương trình tương ứng:
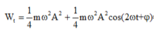
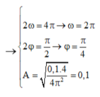
Phương trình dao động là: x = 10 cos 2 πt + π 4 c m
Đúng 0
Bình luận (0)
Phương trình dao động của một vật có dạng
x
A
sin
ω
t
+
A
cos
ω
t
. Biên độ dao động của vật là A.
A
/
2
B.
2
A
C.
A
2
D.
A
3
Đọc tiếp
Phương trình dao động của một vật có dạng x = A sin ω t + A cos ω t . Biên độ dao động của vật là
A. A / 2
B. 2 A
C. A 2
D. A 3
một vật thực hiện đồng thời hai dao động điều hòa có phương trình dao động lần lượt là x15cos(wt + phi)cm và x2A2cos(wt- pi/4) thì dao động tổng hợp có phương trình dao động là xA cos(wt- pi/12). để biên độ A có giá trị bằng một nữa giá trị cực đại Amax của chính nó thì biên độ A2 có giá trị làA.5/căn 3 B.10/căn 3 C.10 căn 3 D.5 căn 3
Đọc tiếp
một vật thực hiện đồng thời hai dao động điều hòa có phương trình dao động lần lượt là x1=5cos(wt + phi)cm và x2=A2cos(wt- pi/4) thì dao động tổng hợp có phương trình dao động là x=A cos(wt- pi/12). để biên độ A có giá trị bằng một nữa giá trị cực đại Amax của chính nó thì biên độ A2 có giá trị là
A.5/căn 3 B.10/căn 3 C.10 căn 3 D.5 căn 3
\(x_1 = 5 \cos (\omega t + \varphi)cm.\)
\(x_2 = A_2 \cos (\omega t - \frac{\pi}{4})cm.\)
\(x= A \cos (\omega t - \frac{\pi}{12})cm.\)
Vẽ giản đồ véc tơ như hình vẽ
Áp dụng định lý hàm số Sin ta có:
Xét: \(\triangle OA_1A:\) \(\frac{A}{\sin OA_1A} = \frac{A_1}{\sin OAA_1} \)
=> \(\frac{A}{\sin (\frac{3\pi}{4}-\varphi)} = \frac{A_1}{\sin (\frac{\pi}{6})} \)
=> \(A= \frac{A_1}{\sin (\frac{\pi}{6})} .\sin (\frac{3\pi}{4}-\varphi).(*)\)
TH1: \(A= A _{max} <=> \sin (\frac{3\pi}{4}-\varphi) = 1\)
=> \(A_{max}= \frac{A_1}{\sin (\frac{\pi}{6})}= 10cm.(1)\)
TH2: \(A = \frac{A_{max}}{2} => \sin (\frac{3\pi}{4}-\varphi) = \frac{1}{2}.\)
=> \(\frac{3\pi}{4} - \varphi = \frac{\pi}{6}\)
=> \(\varphi = \frac{7\pi}{12}.(2)\)
Xét: \(\triangle OA_2A:\) \(\frac{A}{\sin OA_2A} = \frac{A_2}{\sin OAA_2} \)
=> \(\frac{A}{\sin (\frac{3\pi}{4}-\varphi)} = \frac{A_2}{\sin (\varphi+\frac{\pi}{12})} \)
=> \(A_2= \frac{A_{max}}{\sin (\frac{3\pi}{4}-\varphi)} .\sin (\frac{\pi}{12}+\varphi).(3)\)
Thay \((1); (2)\) vào \((3)\) ta được: \(A_2= \frac{10}{0,5} .\sin (\frac{\pi}{12}+\frac{7\pi}{12}) = \frac{10}{0,5}.\frac{\sqrt{3}}{2} = 10 \sqrt{3}cm.\)
Chọn đáp án.C.\(10\sqrt{3}cm.\)
Đúng 0
Bình luận (0)
Bạn kiểm tra lại xem giả thiết còn thiếu gì không?
Đúng 0
Bình luận (0)
mình đánh đủ dữ kiện của đề rồi đó bạn :)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Một vật dao động điều hòa theo phương trình có dạng
x
A
cos
(
ω
t
+
φ
)
. Vật có biên độ dao động bằng 6 cm, pha ban đầu bằng
π
/
6
, tần số dao động
6
Hz. Phương trình vận tốc của dao động là A.
v
6
π
t
6
(
π
6...
Đọc tiếp
Một vật dao động điều hòa theo phương trình có dạng x = A cos ( ω t + φ ) . Vật có biên độ dao động bằng 6 cm, pha ban đầu bằng π / 6 , tần số dao động 6 Hz. Phương trình vận tốc của dao động là
A. v = 6 π t 6 ( π 6 t + π / 6 ) c m
B. v = 24 π t 6 ( 2 π 6 t + π / 6 ) c m
C. v = - 6 π t 6 ( π 6 t + π / 6 ) c m
D. v = - 12 π t 6 ( π 6 t + π / 6 ) c m
Một vật dao động điều hòa theo phương trình có dạng x Acos(ωt+φ). Vật có biên độ dao động bằng 6 cm, pha ban đầu bằng π/6, tần số dao động
6
Hz. Phương trình vận tốc của dao động là
Đọc tiếp
Một vật dao động điều hòa theo phương trình có dạng x = Acos(ωt+φ). Vật có biên độ dao động bằng 6 cm, pha ban đầu bằng π/6, tần số dao động 6 Hz. Phương trình vận tốc của dao động là
