hình cho biết a//b và B1 = 40 độ a) Tính A4 b) So sánh A3 và B2 C) Tính B4
Trên hình biết a // b và góc B2=40 độ:
a) Tính góc A1
b) So sánh góc A3 và B1
c) Tính góc A2+B1
\(a,a//b\Rightarrow\widehat{B_2}+\widehat{A_1}=180^0\left(trong.cùng.phía\right)\\ \Rightarrow\widehat{A_1}=180^0-40^0=140^0\\ b,a//b\Rightarrow\widehat{A_1}=\widehat{B_1}\left(đồng.vị\right)\\ Mà.\widehat{A_1}=\widehat{A_3}\left(đối.đỉnh\right)\\ \Rightarrow\widehat{A_3}=\widehat{B_1}\\ c,Ta.có.\widehat{A_2}+\widehat{B_1}=\widehat{A_2}+\widehat{A_1}=180^0\left(kề.bù\right)\)
a. Ta có: a // b
=> \(\widehat{B_2}+\widehat{A_1}=180^o\) (2 góc trong cùng phía)
Mà \(\widehat{B_2}=40^o\)
=> \(\widehat{A_1}=180^o-40^o=140^o\)
b. Ta có: \(\widehat{A_1}=\widehat{B_3}\) (so le trong) (1)
Ta lại có: \(\left\{{}\begin{matrix}\widehat{A_1}=\widehat{A_3}\left(ĐĐ\right)\\\widehat{B_1}=\widehat{B_3}\left(ĐĐ\right)\end{matrix}\right.\) (2)
Từ (1) và (2), suy ra:
\(\widehat{A_3}=\widehat{B_1}\)
c. Ta có: a // b
=> \(\widehat{A_1}=\widehat{B_1}=140^o\) (đồng vị)
\(\widehat{B_2}=\widehat{A_2}=40^o\) (đồng vị)
=> \(\widehat{A_2}+\widehat{B_1}=140^o+40^o=180^o\)
Cho hình vẽ,biết a // b và góc B1=55 độ.
Tính các góc A1,A2,A3,A4,B2,B3,B4
A1=55o (đồng vị); A2=180o-55o=125o (kề bù với A1); A3=55o (đối đỉnh với A1); A4=125o (đối đỉnh với A2);
B2=125o (đồng vị với A2); B3=55o (đối đỉnh với B1); B4=125o (đối đỉnh với B2)
Cho biết a//b và A4 = 37o
a) Tính góc B1
b) So sánh góc A1 và góc B4
c) Tính góc B2
A/tính góc B1
A4=A1=37 o(2 góc đối đỉnh)
A1=B1= 37o( sole trong)
B/
A1 và B4 ở vị trí trong cùng phía ( bù nhau )
=>A1+B4=180o
=>35+B4=180o
=>B4=180-35
=>B4=145o
C/
Vì B4 và B2 đối đình(bằng nhau)
=> B4=B2=145o
học tốt ><
Hình 22 cho biết a // b và A4 = 37'( độ )
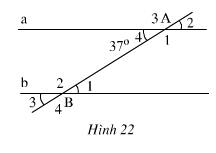
a) Tính B1
b) So sánh A1 và B4
c) Tính B2
a, a//b \(\Rightarrow\widehat{A_4}=\widehat{B_1}=37^0\left(so.le.trong\right)\)
b, a//b \(\Rightarrow\widehat{A_1}=\widehat{B_4}\left(đồng.vị\right)\)
c, \(\widehat{B_2}+\widehat{B_1}=180^0\left(kề.bù\right)\Rightarrow\widehat{B_2}=180^0-37^0=143^0\)
a) Ta có: a//b
⇒A4=B1=370(so le trong)
b) Ta thấy a//b
A1 và B4 là 2 góc đồng vị
⇒A1=B4
c) Ta lại có: A4+B2=1800(trong cùng phía)
⇒370+B2=1800
⇒B2=1800-370=1430
Cho góc A4 = 37độ , a // b , a) tính B1 , b) so sánh A1 và B4 , c) tính B2 . Giải thích cho mình hiểu nha , cảm ơn
Cho hình vẽ sau,biết:A1=B1
a) So sánh các cặp góc đồng vị?
b) So sánh các cặp góc so le trong?
c) Tính A4 +B1;A3 và B2. Nêu nhận xét.
Các cặp góc đồng vị và so le trong và so le ngoài luôn bằng nhau
Còn các cặp góc trong cùng phía và ngoài cùng phía thì bù nhau
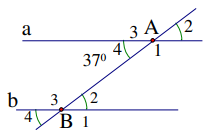 Bài 3. Cho hình 2 biết a // b và A4 = 370. a) Tính B2 . b) So sánh A1 và B1. c) Tính B3
Bài 3. Cho hình 2 biết a // b và A4 = 370. a) Tính B2 . b) So sánh A1 và B1. c) Tính B3
a. \(A_4=B_2=37^0\left(slt\right)\)
b. \(A_1=B_1\left(dongvi\right)\)
c. \(B_3=180^0-B_2=180^0-37^0=143^0\left(kebu\right)\)
cho hình vẽ biết góc A3+B1=180 độ,hãy so sánh góc A4 và B1?,góc A1 và B2, Góc A2 và B3
Trên hình biết a // b và góc B2=40 độ:
a) Tính góc A1
b) So sánh góc A3 và B1
c) Tính góc A2+B1